What Is Half Of 34
dulhadulhi
Sep 23, 2025 · 6 min read
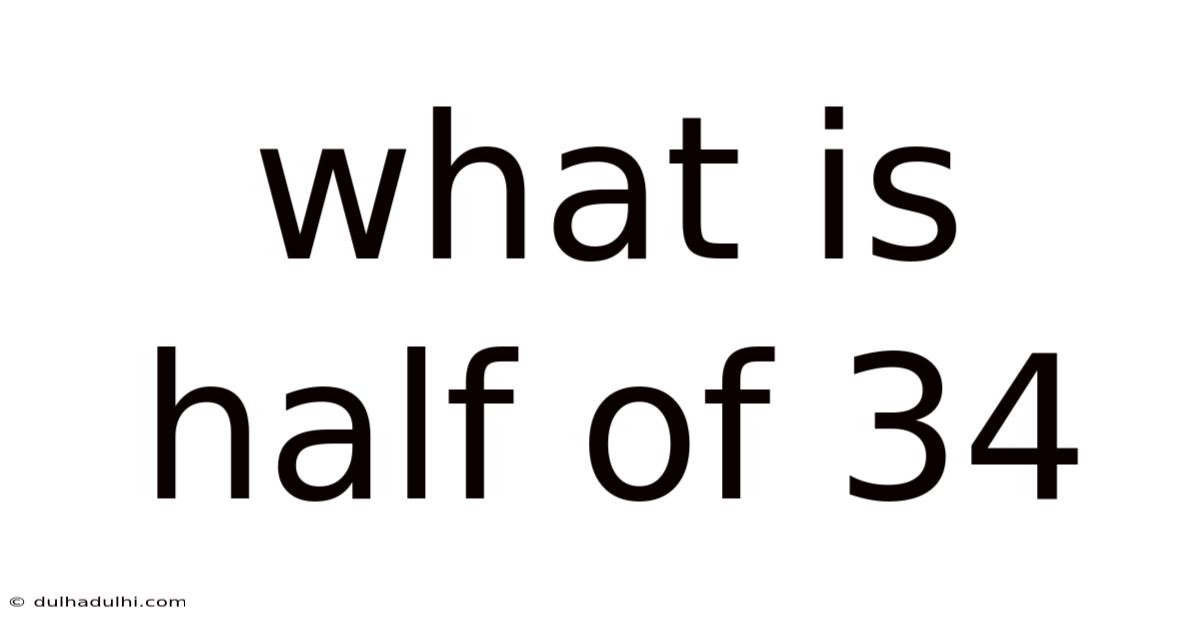
Table of Contents
What is Half of 34? A Deep Dive into Division and Fractions
Finding half of a number is a fundamental concept in mathematics, crucial for everyday life, from splitting bills to understanding proportions. This seemingly simple question, "What is half of 34?", opens the door to exploring various mathematical approaches and their applications. This article will not only answer the question directly but also delve into the underlying principles of division and fractions, providing a comprehensive understanding for learners of all levels.
Understanding the Concept of "Half"
Before we tackle the specific problem, let's solidify our understanding of the term "half." Half simply means one of two equal parts. When we say "half of 34," we're asking what number, when added to itself, equals 34. This inherently involves the concept of division, specifically dividing by 2.
Method 1: Direct Division
The most straightforward method to find half of 34 is to divide 34 by 2. This can be represented mathematically as:
34 ÷ 2 = ?
Performing the division, we find:
34 ÷ 2 = 17
Therefore, half of 34 is 17.
Method 2: Fraction Representation
Another way to approach this problem is through fractions. "Half" can be represented as the fraction 1/2. To find half of 34, we multiply 34 by 1/2:
34 x (1/2) = ?
Multiplying the numerator (top number) and dividing by the denominator (bottom number), we get:
(34 x 1) / 2 = 34 / 2 = 17
Again, we arrive at the answer: half of 34 is 17.
Method 3: Repeated Subtraction
While less efficient for larger numbers, we can also find half of 34 through repeated subtraction. We repeatedly subtract 2 from 34 until we reach 0, counting the number of subtractions. Each subtraction represents one of the two equal parts.
- 34 - 2 = 32
- 32 - 2 = 30
- 30 - 2 = 28
- 28 - 2 = 26
- 26 - 2 = 24
- 24 - 2 = 22
- 22 - 2 = 20
- 20 - 2 = 18
- 18 - 2 = 16
- 16 - 2 = 14
- 14 - 2 = 12
- 12 - 2 = 10
- 10 - 2 = 8
- 8 - 2 = 6
- 6 - 2 = 4
- 4 - 2 = 2
- 2 - 2 = 0
We performed 17 subtractions, confirming that half of 34 is 17.
Expanding the Concept: Halving Larger Numbers
The methods described above can be applied to find half of any number. Let's consider finding half of larger numbers:
- Half of 100: 100 ÷ 2 = 50
- Half of 500: 500 ÷ 2 = 250
- Half of 1000: 1000 ÷ 2 = 500
These examples demonstrate the consistent application of division by 2 to find half of a number.
Understanding Fractions and Their Relationship to Division
The concept of "half" is intimately linked to fractions. A fraction represents a part of a whole. The fraction 1/2 represents one part out of two equal parts. Multiplying a number by 1/2 is equivalent to dividing that number by 2. This fundamental relationship is essential for understanding proportions and ratios.
Real-World Applications of Finding Half
Finding half of a number is a frequently used skill in various real-world scenarios:
- Sharing equally: Dividing a pizza, a bag of candy, or any resource equally among two people requires finding half.
- Calculating discounts: Many sales offer a 50% discount, which means finding half the original price.
- Measurement conversions: Converting units often involves finding half (e.g., converting feet to yards).
- Recipe adjustments: If a recipe serves four people but you only need to serve two, you'll need to find half the ingredient quantities.
- Financial calculations: Determining half of a budget, investment returns, or profits is essential for financial planning.
Beyond Halving: Exploring Other Fractions
While this article focused on finding half (1/2), the principles extend to other fractions. Finding one-third (1/3), one-quarter (1/4), or any fraction of a number involves similar principles of multiplication or division. For example:
- One-third of 36: 36 x (1/3) = 12 or 36 ÷ 3 = 12
- One-quarter of 20: 20 x (1/4) = 5 or 20 ÷ 4 = 5
Decimal Representation and Halving
Numbers can also be expressed in decimal form. Finding half of a decimal number involves the same process of division by 2. For instance:
- Half of 34.5: 34.5 ÷ 2 = 17.25
Illustrative Examples: Putting it into Practice
Let's work through a few more examples to solidify our understanding:
Example 1: A group of 34 students needs to be split into two equal teams for a competition. How many students are on each team?
Solution: Half of 34 is 17, so there will be 17 students on each team.
Example 2: A shirt is originally priced at $34. It's on sale for half price. What is the sale price?
Solution: Half of $34 is $17, so the sale price is $17.
Example 3: A recipe calls for 34 grams of flour, but you only want to make half the recipe. How much flour do you need?
Solution: Half of 34 grams is 17 grams, so you need 17 grams of flour.
Frequently Asked Questions (FAQ)
Q: What if I need to find a third or a quarter of 34?
A: To find one-third, you would divide 34 by 3 (34 ÷ 3 ≈ 11.33). To find one-quarter, you would divide 34 by 4 (34 ÷ 4 = 8.5).
Q: Can I use a calculator to find half of a number?
A: Yes, you can simply divide the number by 2 using a calculator.
Q: Is there a shortcut for finding half of even numbers?
A: For even numbers, you can simply divide the number by 2 mentally by halving each digit (if possible), or moving the decimal point one place to the left. This is because dividing by 2 is the same as multiplying by 0.5.
Q: What if the number is odd? Does finding half still work?
A: Yes, finding half of an odd number will result in a decimal or a fraction. For example, half of 35 is 17.5 or 17 1/2.
Conclusion
Finding half of 34, or any number for that matter, is a fundamental arithmetic skill with broad applications. This seemingly simple calculation opens doors to understanding division, fractions, and their significance in various real-world contexts. Through different approaches – direct division, fractional representation, and repeated subtraction – we've explored multiple pathways to reach the same answer: half of 34 is 17. This knowledge empowers you not just to solve simple problems but to confidently tackle more complex mathematical challenges involving proportions, ratios, and percentages. Mastering this concept strengthens your mathematical foundation and enhances your ability to solve real-world problems effectively. Remember, understanding the "why" behind the calculations is just as important as knowing the "how."
Latest Posts
Latest Posts
-
How Long Lives A Butterfly
Sep 23, 2025
-
Can Elements Be Broken Down
Sep 23, 2025
-
Lcm Of 24 And 84
Sep 23, 2025
-
Integrals Of Inverse Trig Functions
Sep 23, 2025
-
Lcm 3 4 And 5
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about What Is Half Of 34 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.