Lcm Of 24 And 84
dulhadulhi
Sep 23, 2025 · 6 min read
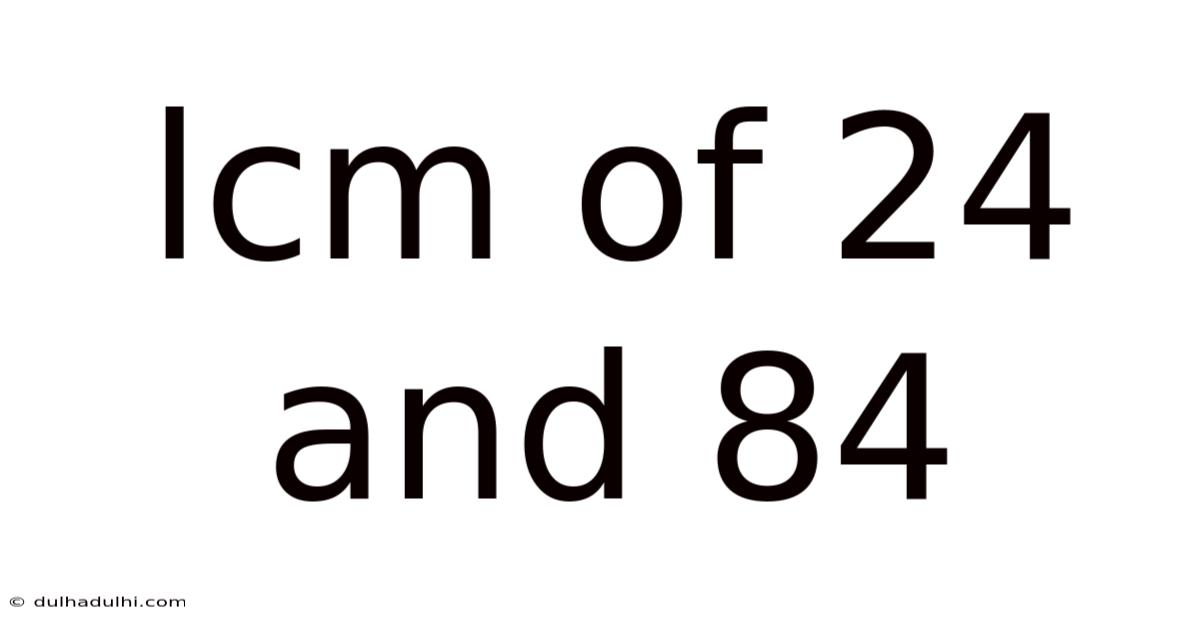
Table of Contents
Finding the Least Common Multiple (LCM) of 24 and 84: A Comprehensive Guide
Finding the least common multiple (LCM) might seem like a simple arithmetic task, but understanding the underlying principles and various methods for calculating it unlocks a deeper appreciation for number theory. This comprehensive guide will explore the LCM of 24 and 84, providing multiple approaches – from prime factorization to the Euclidean algorithm – and clarifying the practical applications of this fundamental concept. We'll also delve into related concepts like the greatest common divisor (GCD) and explore how these concepts connect to other areas of mathematics.
Understanding Least Common Multiples (LCM)
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers. Think of it as the smallest number that contains all the given numbers as factors. For example, the LCM of 2 and 3 is 6 because 6 is the smallest number divisible by both 2 and 3. Finding the LCM is crucial in various mathematical applications, including simplifying fractions, solving problems involving cycles or periodic events, and working with ratios and proportions.
Method 1: Prime Factorization
This is arguably the most straightforward method for finding the LCM, especially for smaller numbers. It involves breaking down each number into its prime factors.
Step 1: Find the prime factorization of each number.
- 24: 24 = 2 x 2 x 2 x 3 = 2³ x 3¹
- 84: 84 = 2 x 2 x 3 x 7 = 2² x 3¹ x 7¹
Step 2: Identify the highest power of each prime factor present in either factorization.
Looking at the prime factorizations above, we have the prime factors 2, 3, and 7.
- The highest power of 2 is 2³ = 8
- The highest power of 3 is 3¹ = 3
- The highest power of 7 is 7¹ = 7
Step 3: Multiply the highest powers together.
LCM(24, 84) = 2³ x 3 x 7 = 8 x 3 x 7 = 168
Therefore, the least common multiple of 24 and 84 is 168. This means 168 is the smallest positive integer divisible by both 24 and 84.
Method 2: Listing Multiples
This method is suitable for smaller numbers where listing multiples is feasible.
Step 1: List the multiples of each number.
- Multiples of 24: 24, 48, 72, 96, 120, 144, 168, 192, ...
- Multiples of 84: 84, 168, 252, ...
Step 2: Identify the smallest common multiple.
By comparing the lists, we can see that the smallest multiple common to both lists is 168. Therefore, the LCM(24, 84) = 168.
This method becomes less practical for larger numbers as the lists become extensive and time-consuming to generate.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and GCD (greatest common divisor) are intimately related. There's a formula that elegantly connects them:
LCM(a, b) = (|a x b|) / GCD(a, b)
Where |a x b| represents the absolute value of the product of a and b.
Step 1: Find the GCD of 24 and 84 using the Euclidean Algorithm.
The Euclidean algorithm is an efficient method for finding the GCD. It involves repeatedly applying the division algorithm until the remainder is 0. The last non-zero remainder is the GCD.
- Divide 84 by 24: 84 = 3 x 24 + 12
- Divide 24 by the remainder 12: 24 = 2 x 12 + 0
The last non-zero remainder is 12, so GCD(24, 84) = 12.
Step 2: Apply the LCM formula.
LCM(24, 84) = (24 x 84) / 12 = 2016 / 12 = 168
This method provides an alternative and often more efficient approach, particularly when dealing with larger numbers.
Method 4: Prime Factorization and Venn Diagrams
This method provides a visual representation of the prime factorization approach and is excellent for understanding the relationship between the LCM and GCD.
Step 1: Prime factorize both numbers. (As done in Method 1)
- 24 = 2³ x 3¹
- 84 = 2² x 3¹ x 7¹
Step 2: Create a Venn Diagram
Draw two overlapping circles, one for 24 and one for 84. Place the common prime factors (in this case, 2² and 3¹) in the overlapping region. Place the remaining prime factors in the non-overlapping portions.
- Overlap: 2² x 3¹
- 24 only: 2¹
- 84 only: 7¹
Step 3: Calculate the LCM and GCD
- LCM: Multiply all the factors in the Venn diagram: 2³ x 3¹ x 7¹ = 168
- GCD: Multiply the factors in the overlapping region: 2² x 3¹ = 12
This visual approach makes it clear how the common factors contribute to both the GCD and the LCM.
Real-World Applications of LCM
The concept of LCM isn't just a theoretical exercise; it has numerous practical applications:
- Scheduling: Imagine two buses leaving a terminal at different intervals. The LCM of their intervals helps determine when they'll depart together again.
- Fractions: Finding a common denominator when adding or subtracting fractions involves finding the LCM of the denominators.
- Gears and Pulleys: In mechanical systems, the LCM helps calculate the synchronized rotation of gears or pulleys.
- Cyclic Events: Determining when events with different periodicities coincide (like planetary alignments or repeating patterns).
- Construction and Measurement: When dealing with different lengths or measurements needing to align, LCM plays a crucial role.
Frequently Asked Questions (FAQs)
Q: What is the difference between LCM and GCD?
A: The LCM (Least Common Multiple) is the smallest number divisible by all the given numbers. The GCD (Greatest Common Divisor) is the largest number that divides all the given numbers without leaving a remainder. They are inversely related; a larger GCD implies a smaller LCM, and vice versa.
Q: Can the LCM of two numbers be smaller than one of the numbers?
A: No. The LCM is always greater than or equal to the larger of the two numbers.
Q: What if one of the numbers is zero?
A: The LCM of any number and zero is undefined. The GCD of any number and zero is the number itself.
Q: Is there a limit to the size of numbers for which the LCM can be calculated?
A: Theoretically, there's no limit, though computational limitations might arise for extremely large numbers. Algorithms like the Euclidean algorithm are designed for efficiency, even with very large integers.
Q: Are there other methods to calculate the LCM besides the ones discussed?
A: Yes, there are more advanced algorithms and methods for calculating LCMs, particularly for a larger set of numbers. These often leverage the relationship between LCM and GCD and utilize optimized computational approaches.
Conclusion
Finding the least common multiple of 24 and 84, as demonstrated through various methods, highlights the fundamental importance of this concept in mathematics. Understanding the different approaches – prime factorization, listing multiples, using the GCD, and the Venn diagram approach – equips you with diverse tools to tackle LCM problems effectively, irrespective of the numbers' size. The practical applications of the LCM extend beyond the classroom, proving its relevance in various fields, underscoring its value as a core mathematical concept. Mastering the LCM not only strengthens your arithmetic skills but also enhances your problem-solving abilities in diverse real-world scenarios.
Latest Posts
Latest Posts
-
Measurement Of Intensity Of Sound
Sep 23, 2025
-
90 Degrees F In C
Sep 23, 2025
-
Words With The Ly Suffix
Sep 23, 2025
-
Example Of A Contact Force
Sep 23, 2025
-
How Do You Do Indices
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 24 And 84 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.