Sin 2 Cos 2 1
dulhadulhi
Sep 23, 2025 · 6 min read
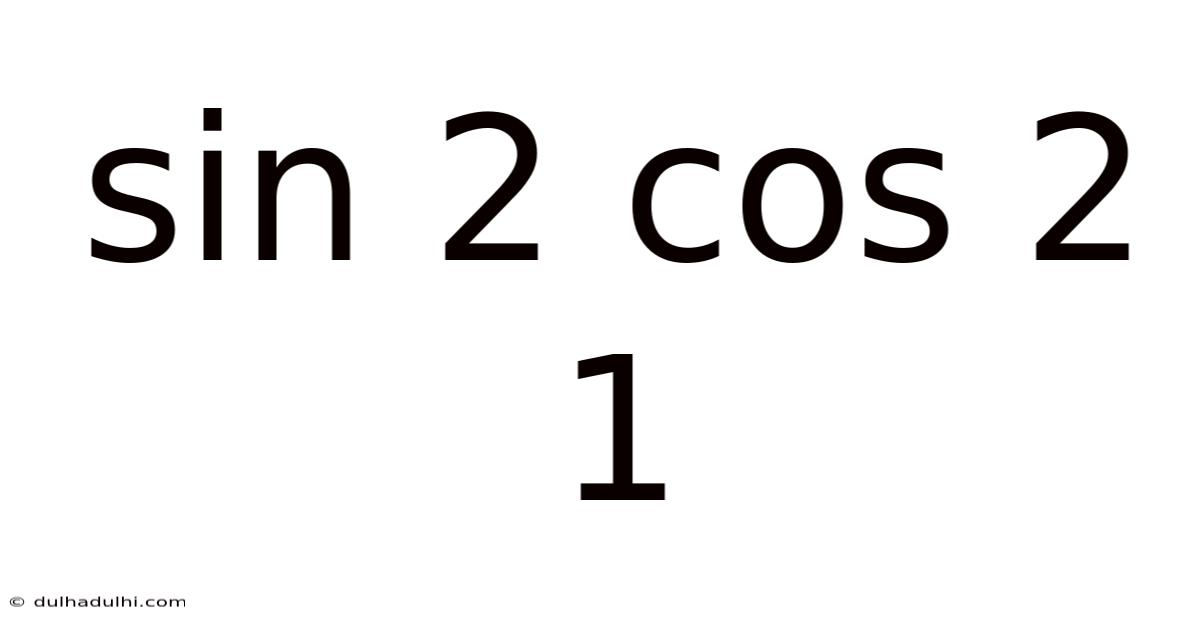
Table of Contents
Decoding the Trigonometric Identity: sin²x + cos²x = 1
This article delves into the fundamental trigonometric identity, sin²x + cos²x = 1, exploring its proof, applications, and significance in various mathematical fields. We'll move beyond a simple statement of the identity to understand its deep implications and how it underpins more complex trigonometric relationships. This comprehensive guide will equip you with a robust understanding of this cornerstone of trigonometry.
Introduction: The Pythagorean Theorem's Trigonometric Cousin
The identity sin²x + cos²x = 1 is arguably the most important trigonometric identity. It's a direct consequence of the Pythagorean theorem and forms the basis for numerous other trigonometric relationships. Understanding this identity is crucial for simplifying trigonometric expressions, solving equations, and tackling more advanced topics in calculus and beyond. This identity holds true for any angle x, regardless of whether it's measured in degrees or radians.
Proof of the Identity: From Geometry to Trigonometry
The proof of sin²x + cos²x = 1 elegantly connects geometry and trigonometry. Let's consider a right-angled triangle with hypotenuse of length 1. We label the angle opposite one of the legs as x.
-
Defining Trigonometric Functions: Recall the definitions of sine and cosine:
- sin x = opposite/hypotenuse
- cos x = adjacent/hypotenuse
-
Applying the Definitions: In our right-angled triangle with hypotenuse 1, we have:
- sin x = opposite side length
- cos x = adjacent side length
-
Pythagorean Theorem: The Pythagorean theorem states that the square of the hypotenuse is equal to the sum of the squares of the other two sides. In our triangle, this translates to:
(opposite side length)² + (adjacent side length)² = (hypotenuse)²
-
Substituting Trigonometric Functions: Substituting our definitions of sin x and cos x, we get:
(sin x)² + (cos x)² = (1)²
-
Simplifying: This simplifies to the fundamental identity:
sin²x + cos²x = 1
Visualizing the Identity: The Unit Circle
The unit circle provides a powerful visual representation of the sin²x + cos²x = 1 identity. The unit circle is a circle with a radius of 1 centered at the origin of a coordinate plane.
-
Coordinates and Trigonometric Functions: Any point on the unit circle can be represented by its coordinates (cos x, sin x), where x is the angle formed between the positive x-axis and the line connecting the origin to that point.
-
Pythagorean Theorem on the Unit Circle: The distance from the origin to any point on the unit circle is always 1 (the radius). Using the Pythagorean theorem with the coordinates (cos x, sin x), we have:
(cos x)² + (sin x)² = 1²
-
The Identity Confirmed: This again confirms the identity sin²x + cos²x = 1. This visual representation highlights the relationship between the angle x and the coordinates on the unit circle, providing a geometric understanding of the identity.
Applications of the Identity: A Foundation for Trigonometric Calculations
The sin²x + cos²x = 1 identity is not just a theoretical result; it's a fundamental tool used extensively in various mathematical contexts. Here are some key applications:
-
Simplifying Trigonometric Expressions: This identity is invaluable for simplifying complex trigonometric expressions. By strategically using the identity, you can often reduce intricate expressions into simpler forms, making calculations easier and more manageable.
-
Solving Trigonometric Equations: Many trigonometric equations can be solved more easily by applying the sin²x + cos²x = 1 identity. It allows you to rewrite equations in terms of a single trigonometric function, making them significantly simpler to solve.
-
Deriving Other Trigonometric Identities: The fundamental identity acts as a cornerstone for deriving numerous other trigonometric identities. Many more complex relationships can be traced back to this core identity.
-
Calculus: In calculus, the identity is crucial in differentiation and integration involving trigonometric functions. It helps simplify expressions and solve problems involving trigonometric derivatives and integrals.
Beyond the Basics: Related Identities and Their Derivations
The sin²x + cos²x = 1 identity leads to several other important trigonometric identities. Let's explore some key derivations:
-
Derivation of tan²x + 1 = sec²x: We begin with the identity sin²x + cos²x = 1. Dividing both sides of the equation by cos²x, assuming cos x ≠ 0, we get:
sin²x/cos²x + cos²x/cos²x = 1/cos²x
This simplifies to:
tan²x + 1 = sec²x
-
Derivation of 1 + cot²x = csc²x: Similarly, dividing both sides of sin²x + cos²x = 1 by sin²x, assuming sin x ≠ 0, we obtain:
sin²x/sin²x + cos²x/sin²x = 1/sin²x
This simplifies to:
1 + cot²x = csc²x
Practical Examples: Putting the Identity into Action
Let's illustrate the practical application of the sin²x + cos²x = 1 identity with a couple of examples.
Example 1: Simplifying a Trigonometric Expression
Simplify the expression: sin⁴x + 2sin²xcos²x + cos⁴x
Solution: Notice that this expression resembles the expansion of (a + b)². We can rewrite the expression as:
(sin²x + cos²x)²
Since sin²x + cos²x = 1, the expression simplifies to:
(1)² = 1
Example 2: Solving a Trigonometric Equation
Solve the equation: 2sin²x - cos²x = 1
Solution: We can use the identity sin²x + cos²x = 1 to rewrite cos²x as 1 - sin²x. Substituting this into the equation gives:
2sin²x - (1 - sin²x) = 1
Simplifying and solving for sin²x:
3sin²x = 2
sin²x = 2/3
sin x = ±√(2/3)
This gives us the solutions for x.
Frequently Asked Questions (FAQ)
Q1: Is this identity only valid for acute angles?
A1: No, the identity sin²x + cos²x = 1 is valid for all angles x, whether acute, obtuse, or reflex, including negative angles. This is because the definitions of sine and cosine are extended to all angles using the unit circle.
Q2: What happens if I divide by zero when deriving other identities?
A2: When deriving identities like tan²x + 1 = sec²x or 1 + cot²x = csc²x, we must explicitly state the condition that we are not dividing by zero. This means cos x ≠ 0 for the tangent/secant identity and sin x ≠ 0 for the cotangent/cosecant identity. These restrictions ensure the validity of the derived identities.
Q3: How does this identity relate to other branches of mathematics?
A3: The sin²x + cos²x = 1 identity has far-reaching implications beyond trigonometry. It finds applications in complex analysis, differential equations, and even physics, particularly in areas involving oscillations and waves. Its fundamental nature makes it a crucial tool in many mathematical fields.
Q4: Are there other fundamental trigonometric identities?
A4: Yes, besides sin²x + cos²x = 1, several other identities are fundamental, including the sum and difference formulas for sine and cosine, double-angle formulas, and half-angle formulas. These identities, along with the fundamental one, form the core of trigonometric manipulation and problem-solving.
Conclusion: The Enduring Power of a Simple Identity
The trigonometric identity sin²x + cos²x = 1 is far more than a simple equation; it's a fundamental pillar of trigonometry and a gateway to understanding more complex mathematical concepts. Its elegant proof, versatile applications, and connections to other identities highlight its significance. Mastering this identity is not only crucial for success in trigonometry but also paves the way for deeper exploration into calculus, analysis, and various branches of applied mathematics and physics. Through understanding this seemingly simple equation, one gains a powerful tool for solving problems and unlocking the beauty of mathematical relationships.
Latest Posts
Latest Posts
-
What Are Factors For 33
Sep 23, 2025
-
Biggest Gland In Human Body
Sep 23, 2025
-
Lcm For 7 And 9
Sep 23, 2025
-
Greek Numbers 1 To 10
Sep 23, 2025
-
Can Ionic Compounds Conduct Electricity
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about Sin 2 Cos 2 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.