Lcm For 7 And 9
dulhadulhi
Sep 23, 2025 · 6 min read
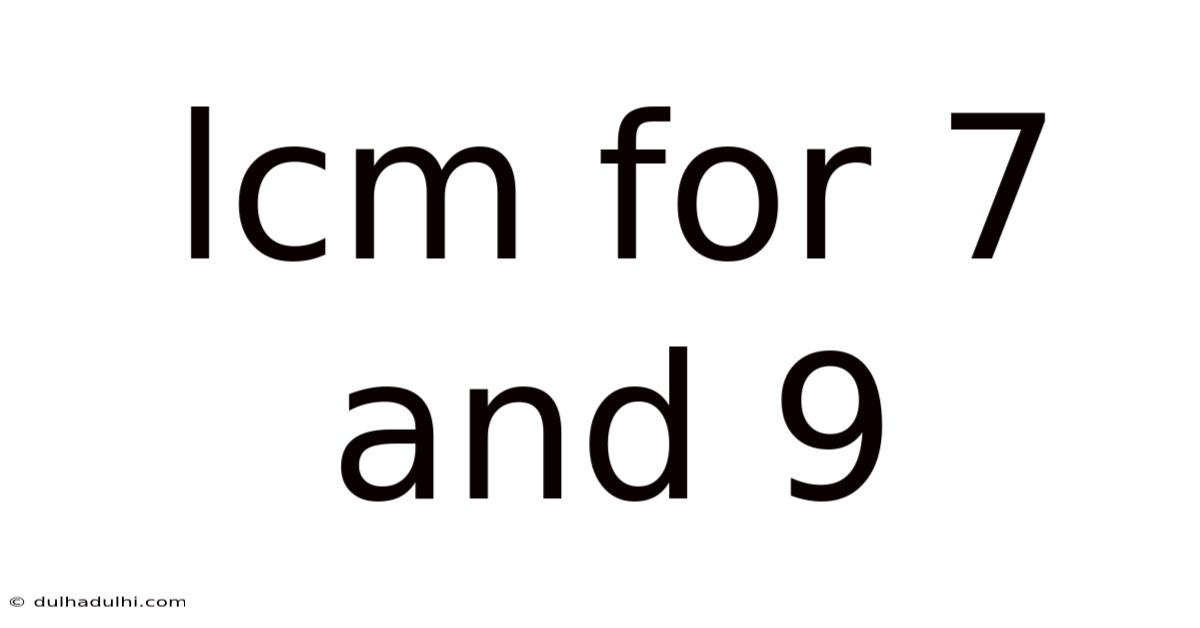
Table of Contents
Finding the Least Common Multiple (LCM) of 7 and 9: A Comprehensive Guide
Finding the least common multiple (LCM) is a fundamental concept in mathematics, crucial for solving problems involving fractions, ratios, and cycles. This article will comprehensively explore how to find the LCM of 7 and 9, employing various methods, and delve into the underlying mathematical principles. We'll also explore the broader significance of LCMs and answer frequently asked questions. Understanding LCMs is vital for students and anyone working with numerical relationships.
Understanding Least Common Multiples (LCM)
Before we tackle the specific LCM of 7 and 9, let's establish a clear understanding of what an LCM actually is. The least common multiple of two or more integers is the smallest positive integer that is divisible by all the integers. Think of it as the smallest number that contains all the given numbers as factors. For example, the LCM of 2 and 3 is 6 because 6 is the smallest positive integer divisible by both 2 and 3.
Method 1: Listing Multiples
This is a straightforward method, particularly useful for smaller numbers like 7 and 9. We simply list the multiples of each number until we find the smallest multiple common to both.
- Multiples of 7: 7, 14, 21, 28, 35, 42, 49, 56, 63, 70, 77, ...
- Multiples of 9: 9, 18, 27, 36, 45, 54, 63, 72, 81, ...
Notice that 63 appears in both lists. Therefore, the LCM of 7 and 9 is 63. This method is effective for smaller numbers, but becomes less practical as the numbers get larger.
Method 2: Prime Factorization
This is a more powerful and efficient method, especially for larger numbers. It leverages the fundamental theorem of arithmetic, which states that every integer greater than 1 can be uniquely represented as a product of prime numbers.
-
Find the prime factorization of each number:
- 7 is a prime number, so its prime factorization is simply 7.
- 9 = 3 x 3 = 3².
-
Identify the highest power of each prime factor:
- The prime factors involved are 3 and 7.
- The highest power of 3 is 3² = 9.
- The highest power of 7 is 7¹ = 7.
-
Multiply the highest powers together:
- LCM(7, 9) = 3² x 7 = 9 x 7 = 63
This method provides a systematic approach that works for any pair of integers, regardless of their size. It's also easier to understand and implement for larger numbers than listing multiples.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and the greatest common divisor (GCD) of two numbers are related through a simple formula:
LCM(a, b) = (|a x b|) / GCD(a, b)
where |a x b| represents the absolute value of the product of a and b.
-
Find the GCD of 7 and 9:
Since 7 and 9 share no common factors other than 1, their GCD is 1.
-
Apply the formula:
LCM(7, 9) = (7 x 9) / GCD(7, 9) = 63 / 1 = 63
This method is efficient if you already know the GCD of the two numbers. Finding the GCD can be done using the Euclidean algorithm, another efficient method for finding the greatest common divisor of two integers. The Euclidean algorithm is particularly useful when dealing with larger numbers.
The Euclidean Algorithm for Finding the GCD
The Euclidean algorithm is a highly efficient method for finding the GCD of two integers. Let's illustrate with an example using numbers larger than 7 and 9: Let's find the GCD of 48 and 18.
-
Divide the larger number by the smaller number and find the remainder: 48 ÷ 18 = 2 with a remainder of 12.
-
Replace the larger number with the smaller number, and the smaller number with the remainder: Now we find the GCD of 18 and 12.
-
Repeat the process: 18 ÷ 12 = 1 with a remainder of 6.
-
Continue until the remainder is 0: 12 ÷ 6 = 2 with a remainder of 0.
The last non-zero remainder is the GCD. In this case, the GCD(48, 18) = 6. This method is significantly faster than trial and error for larger numbers.
Once you have the GCD, you can use the formula mentioned earlier to calculate the LCM.
Real-World Applications of LCM
Understanding LCMs is not just an academic exercise; it has practical applications across various fields:
-
Scheduling: Determining when events will occur simultaneously. For example, if two buses leave a station at different intervals, the LCM helps calculate when they will depart at the same time again.
-
Fraction Operations: Finding the least common denominator (LCD) when adding or subtracting fractions. The LCD is simply the LCM of the denominators.
-
Cycling Problems: Problems involving repetitive cycles, like gear rotations in machinery or the timing of recurring events.
-
Construction and Engineering: In projects requiring synchronized operations or materials with varying lengths or cycles.
Frequently Asked Questions (FAQ)
Q: Is there only one LCM for two numbers?
A: Yes, there is only one least common multiple for any given pair of integers.
Q: What if the numbers are negative?
A: When dealing with negative numbers, we consider the absolute values of the numbers when calculating the LCM. The LCM will always be positive.
Q: Can I use a calculator to find the LCM?
A: Most scientific calculators and many online calculators have built-in functions to calculate the LCM of two or more numbers.
Q: What if I have more than two numbers?
A: The methods described above, particularly prime factorization, can be extended to find the LCM of more than two numbers. You would find the prime factorization of each number, identify the highest power of each prime factor present across all numbers, and then multiply these highest powers together.
Q: Why is understanding LCM important?
A: Understanding LCMs is crucial for various mathematical operations and problem-solving, particularly involving fractions, ratios, and cyclic events. It's a fundamental concept that builds a foundation for more advanced mathematical topics.
Conclusion
Finding the LCM of 7 and 9, whether through listing multiples, prime factorization, or utilizing the GCD, consistently yields the same result: 63. The choice of method depends on the complexity of the numbers involved and the tools available. Prime factorization offers a more robust and efficient approach, especially for larger numbers. Understanding the LCM and its related concepts is essential for anyone working with numerical relationships and problem-solving in various fields. The methods described here provide a solid foundation for tackling more complex LCM problems and grasping the broader significance of this crucial mathematical concept. Remember to practice these methods to solidify your understanding and improve your problem-solving skills.
Latest Posts
Latest Posts
-
Animals In A Food Chain
Sep 23, 2025
-
Net Of A Triangular Prism
Sep 23, 2025
-
Do Table Salt Melt Ice
Sep 23, 2025
-
O2 Dot And Cross Diagram
Sep 23, 2025
-
Can Stress Cause A Uti
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about Lcm For 7 And 9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.