Lcm Of 6 And 10
dulhadulhi
Sep 23, 2025 · 6 min read
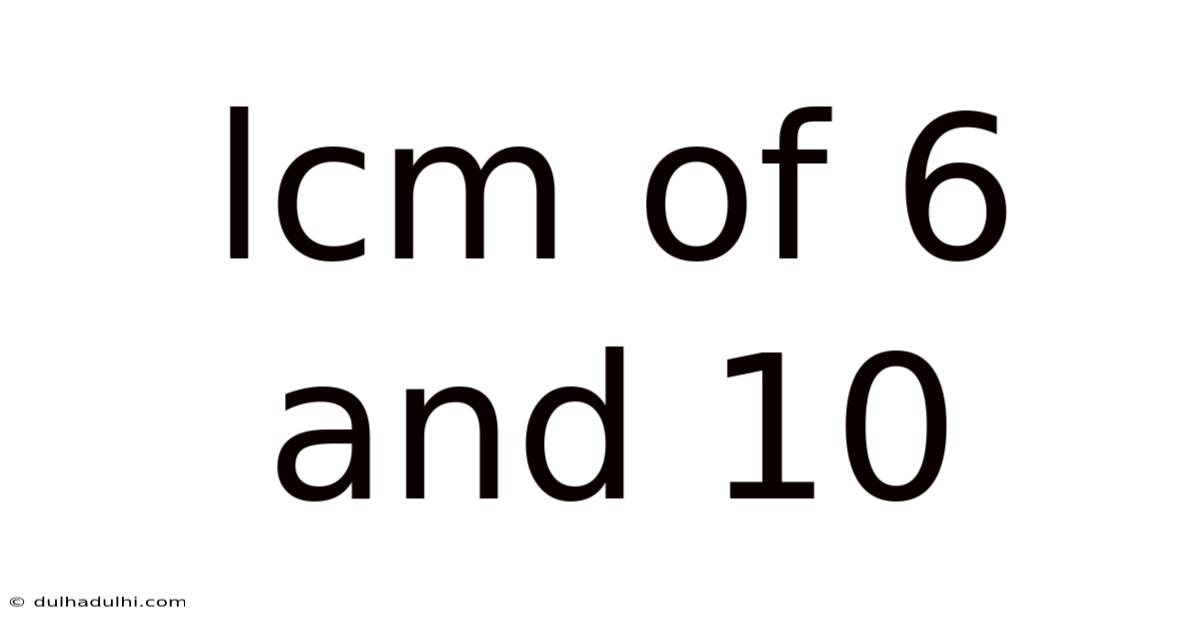
Table of Contents
Unveiling the Least Common Multiple (LCM) of 6 and 10: A Comprehensive Guide
Finding the least common multiple (LCM) might seem like a simple arithmetic task, but understanding the underlying concepts opens doors to more complex mathematical ideas. This comprehensive guide delves into calculating the LCM of 6 and 10, exploring various methods, their applications, and providing a solid foundation for understanding LCMs in broader mathematical contexts. We'll move beyond simple calculation and explore the "why" behind the process, ensuring you grasp the fundamental principles.
Introduction: What is the Least Common Multiple (LCM)?
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers. In simpler terms, it's the smallest number that contains all the numbers as factors. Understanding LCMs is crucial in various mathematical applications, including simplifying fractions, solving problems involving ratios and proportions, and even in more advanced areas like abstract algebra. This article focuses on finding the LCM of 6 and 10, using multiple approaches to solidify your understanding.
Method 1: Listing Multiples
This is a straightforward method, particularly useful for smaller numbers. Let's list the multiples of 6 and 10:
- Multiples of 6: 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, ...
- Multiples of 10: 10, 20, 30, 40, 50, 60, 70, 80, 90, 100, ...
By comparing the two lists, we can identify the common multiples: 30, 60, and so on. The smallest of these common multiples is 30. Therefore, the LCM of 6 and 10 is 30.
This method is effective for smaller numbers, but it becomes cumbersome and inefficient when dealing with larger numbers or a greater number of integers.
Method 2: Prime Factorization
This method is more efficient and works well for larger numbers. It involves finding the prime factorization of each number. Prime factorization is expressing a number as a product of its prime factors (numbers divisible only by 1 and themselves).
- Prime factorization of 6: 2 x 3
- Prime factorization of 10: 2 x 5
Now, we identify the highest power of each prime factor present in either factorization:
- The highest power of 2 is 2¹ = 2
- The highest power of 3 is 3¹ = 3
- The highest power of 5 is 5¹ = 5
To find the LCM, we multiply these highest powers together: 2 x 3 x 5 = 30. Thus, the LCM of 6 and 10 is again 30. This method is more systematic and less prone to error, especially when dealing with larger numbers.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and the greatest common divisor (GCD) are closely related. The GCD of two numbers is the largest number that divides both without leaving a remainder. There's a useful formula connecting the LCM and GCD:
LCM(a, b) = (|a x b|) / GCD(a, b)
First, let's find the GCD of 6 and 10 using the Euclidean algorithm:
- Divide the larger number (10) by the smaller number (6): 10 ÷ 6 = 1 with a remainder of 4.
- Replace the larger number with the smaller number (6) and the smaller number with the remainder (4): 6 ÷ 4 = 1 with a remainder of 2.
- Repeat the process: 4 ÷ 2 = 2 with a remainder of 0.
- The GCD is the last non-zero remainder, which is 2.
Now, we can use the formula:
LCM(6, 10) = (6 x 10) / GCD(6, 10) = 60 / 2 = 30
This method provides an alternative approach, particularly useful when the GCD is easily determined.
Method 4: Venn Diagram Approach (Visual Representation)
While not a direct calculation method, a Venn diagram can provide a visual understanding of the LCM. We represent the prime factors of each number in separate circles, with the overlapping section showing the common factors.
[Imagine a Venn diagram here with two circles. One circle labeled "6" containing 2 and 3. The other circle labeled "10" containing 2 and 5. The number 2 is in the overlapping section.]
The LCM is found by multiplying all the unique prime factors present in both circles: 2 x 3 x 5 = 30. This visualization helps solidify the understanding of the prime factorization method.
Applications of LCM
Understanding LCMs has far-reaching applications in various fields:
-
Fraction Addition and Subtraction: Finding a common denominator when adding or subtracting fractions requires finding the LCM of the denominators. For example, to add 1/6 and 1/10, we need to find the LCM of 6 and 10 (which is 30), convert the fractions to have a denominator of 30, and then add them.
-
Scheduling Problems: LCM is used to determine when events that repeat at different intervals will occur simultaneously. For instance, if bus A arrives every 6 minutes and bus B arrives every 10 minutes, the LCM (30) indicates they will arrive together every 30 minutes.
-
Music Theory: In music, the LCM is crucial in understanding rhythmic patterns and harmonies. The LCM helps determine the shortest time period after which a rhythmic pattern repeats.
-
Engineering and Construction: LCM is used in various aspects of engineering to coordinate different cycles or processes that must occur in synchronization.
-
Computer Science: LCM plays a role in various algorithms and data structures, particularly in areas dealing with periodic events or processes.
Frequently Asked Questions (FAQ)
-
Q: What is the difference between LCM and GCD?
A: The least common multiple (LCM) is the smallest number divisible by both given numbers, while the greatest common divisor (GCD) is the largest number that divides both given numbers without leaving a remainder. They are inversely related.
-
Q: Can the LCM of two numbers be equal to one of the numbers?
A: Yes, this happens if one number is a multiple of the other. For instance, the LCM of 6 and 12 is 12.
-
Q: How do I find the LCM of more than two numbers?
A: The prime factorization method works well for multiple numbers. Find the prime factorization of each number, then identify the highest power of each prime factor present in any of the factorizations. Multiply these highest powers together to find the LCM.
-
Q: Is there a formula for calculating the LCM directly without using the GCD?
A: While the formula using the GCD is efficient, you can adapt the prime factorization method directly without explicitly calculating the GCD. It simply involves identifying the highest powers of all prime factors found in the factorization of the numbers involved and multiplying those powers together.
Conclusion: Mastering the LCM
Understanding and calculating the LCM is a fundamental skill in mathematics with diverse applications. Whether you use the listing multiples method, prime factorization, the GCD relationship, or the visual Venn diagram approach, the key is to choose the method most appropriate for the given numbers and your comfort level. By mastering these techniques, you will not only solve LCM problems effectively but also gain a deeper appreciation for the underlying mathematical concepts, paving the way for more advanced mathematical explorations. Remember, practice is key to solidifying your understanding and improving your efficiency in calculating LCMs. The more you practice, the more intuitive the process will become. And who knows, you might even start to enjoy the challenge!
Latest Posts
Latest Posts
-
Adaptation Of Camel In Desert
Sep 23, 2025
-
What Is 5 Of 200000
Sep 23, 2025
-
Valence Electron Pair Repulsion Theory
Sep 23, 2025
-
Does Normal Salt Melt Ice
Sep 23, 2025
-
Lcm Of 2 And 3
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 6 And 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.