Lcm Of 2 And 3
dulhadulhi
Sep 23, 2025 · 7 min read
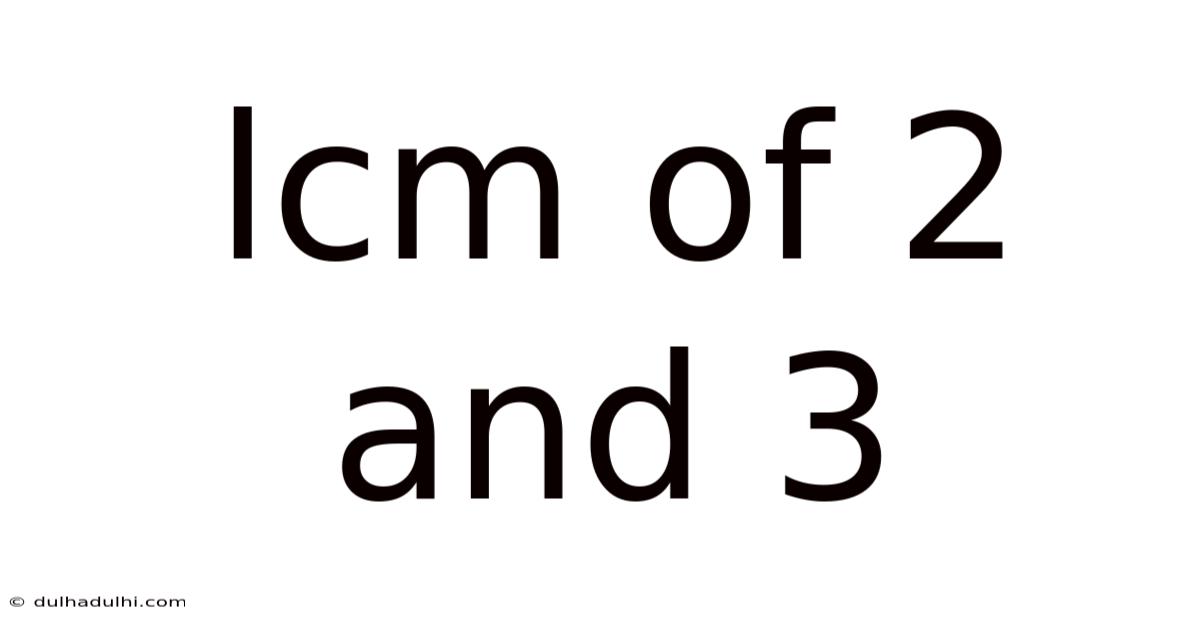
Table of Contents
Understanding the Least Common Multiple (LCM) of 2 and 3: A Deep Dive
Finding the Least Common Multiple (LCM) of two numbers might seem like a simple arithmetic task, especially when dealing with small numbers like 2 and 3. However, understanding the underlying concepts and exploring different methods for calculating the LCM provides a solid foundation for tackling more complex problems in mathematics, particularly in algebra and number theory. This comprehensive guide will not only show you how to find the LCM of 2 and 3 but will also delve into the theoretical underpinnings, explore various calculation methods, and address frequently asked questions.
Introduction: What is the Least Common Multiple?
The Least Common Multiple (LCM) of two or more integers is the smallest positive integer that is a multiple of all the given integers. In simpler terms, it's the smallest number that all the numbers you're considering can divide into evenly. Understanding LCM is crucial in various mathematical operations, including simplifying fractions, solving problems involving ratios and proportions, and working with periodic phenomena.
For example, if we consider the numbers 4 and 6, their multiples are:
- Multiples of 4: 4, 8, 12, 16, 20, 24, 28, 32, 36…
- Multiples of 6: 6, 12, 18, 24, 30, 36…
The common multiples of 4 and 6 are 12, 24, 36, and so on. The smallest common multiple is 12. Therefore, the LCM of 4 and 6 is 12.
Calculating the LCM of 2 and 3: Method 1 - Listing Multiples
The most straightforward method, especially for small numbers, is to list the multiples of each number and identify the smallest common one.
- Multiples of 2: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20…
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24…
By inspecting these lists, we can clearly see that the smallest number appearing in both lists is 6. Therefore, the LCM of 2 and 3 is 6.
This method is simple and intuitive, making it ideal for beginners or when dealing with relatively small numbers. However, it becomes less efficient as the numbers involved get larger.
Calculating the LCM of 2 and 3: Method 2 - Prime Factorization
Prime factorization is a more powerful and efficient method for finding the LCM, especially when dealing with larger numbers. It involves breaking down each number into its prime factors – numbers divisible only by 1 and themselves.
- Prime factorization of 2: 2 (2 is a prime number itself)
- Prime factorization of 3: 3 (3 is also a prime number)
To find the LCM using prime factorization, we follow these steps:
-
Find the prime factorization of each number: As shown above, 2 and 3 are prime numbers, so their prime factorizations are simply themselves.
-
Identify the highest power of each prime factor: Since 2 and 3 are distinct prime numbers, each appears only once with a power of 1.
-
Multiply the highest powers together: The LCM is the product of the highest powers of all the prime factors involved. In this case, it's 2¹ x 3¹ = 2 x 3 = 6.
This method is more systematic and less prone to error, particularly beneficial when dealing with larger numbers that have multiple prime factors.
Calculating the LCM of 2 and 3: Method 3 - Using the Formula with GCD
The Least Common Multiple (LCM) and the Greatest Common Divisor (GCD) are intimately related. There's a formula that elegantly connects them:
LCM(a, b) = (|a * b|) / GCD(a, b)
Where:
aandbare the two numbers.GCD(a, b)is the greatest common divisor ofaandb.|a * b|represents the absolute value of the product of a and b (which is simply the product when dealing with positive integers).
Let's apply this to our problem:
-
Find the GCD of 2 and 3: The greatest common divisor of 2 and 3 is 1 because 1 is the only positive integer that divides both 2 and 3 without leaving a remainder.
-
Apply the formula: LCM(2, 3) = (2 * 3) / GCD(2, 3) = 6 / 1 = 6.
This method highlights the fundamental relationship between LCM and GCD, offering a more advanced approach to calculating the LCM.
The Significance of the LCM of 2 and 3 in Real-World Applications
While the LCM of 2 and 3 might seem trivial in isolation, the concept extends to various real-world applications:
-
Scheduling: Imagine two machines operating in a factory. One machine completes a cycle every 2 hours, and the other every 3 hours. The LCM (6) indicates when both machines will simultaneously complete a cycle, allowing for efficient scheduling of maintenance or material replenishment.
-
Fractions and Ratios: When adding or subtracting fractions, finding the LCM of the denominators is crucial for obtaining a common denominator, simplifying the calculations.
-
Cyclic Patterns: Many natural phenomena exhibit cyclic patterns. The LCM helps determine when these cycles will coincide. For instance, consider two celestial bodies with different orbital periods. The LCM of their periods determines when they will be in the same relative positions.
-
Music Theory: The LCM is used in music theory to determine the least common period of two notes with different frequencies, helping to understand harmonic intervals.
Mathematical Properties of LCM
The LCM possesses several important mathematical properties:
-
Commutative Property: LCM(a, b) = LCM(b, a) – The order of the numbers doesn't affect the result.
-
Associative Property: LCM(a, LCM(b, c)) = LCM(LCM(a, b), c) – You can group the numbers in different ways without altering the outcome.
-
Distributive Property with GCD: LCM(a, GCD(b, c)) = GCD(LCM(a, b), LCM(a, c)) – This property links LCM and GCD in a more complex, but powerful relationship.
Frequently Asked Questions (FAQ)
Q: Is there a difference between LCM and GCD?
A: Yes, there's a significant difference. The LCM (Least Common Multiple) is the smallest number that is a multiple of both given numbers. The GCD (Greatest Common Divisor) is the largest number that divides both given numbers without leaving a remainder. They are inversely related, as shown in the formula: LCM(a, b) = (|a * b|) / GCD(a, b).
Q: Can the LCM of two numbers be one of the numbers?
A: Yes, if one number is a multiple of the other. For example, the LCM of 2 and 4 is 4.
Q: How do I find the LCM of more than two numbers?
A: You can extend the prime factorization method or the formula involving GCD to include more than two numbers. For instance, to find the LCM of 2, 3, and 4, you would find the prime factorization of each number (2, 3, 2²), identify the highest power of each prime factor (2², 3), and multiply them together (4 x 3 = 12).
Q: What if the numbers are negative?
A: When dealing with negative numbers, find the LCM of their absolute values. The LCM will always be a positive integer.
Q: Are there any online calculators or software that can compute LCM?
A: Yes, many online calculators and mathematical software packages can compute the LCM of any set of numbers efficiently. However, understanding the underlying principles and methods is crucial for solving more complex problems and deepening your mathematical understanding.
Conclusion: Beyond the Basics of LCM(2,3)
While finding the LCM of 2 and 3 is a relatively simple calculation, the process illuminates fundamental concepts in number theory. Mastering the different methods for calculating the LCM – listing multiples, prime factorization, and using the GCD relationship – provides a strong foundation for tackling more advanced mathematical problems. Understanding LCM's role in scheduling, fraction simplification, and other applications underscores its practical significance beyond the realm of pure mathematics. By grasping these concepts, you'll not only be able to solve LCM problems efficiently but also appreciate the interconnectedness of various mathematical ideas. The seemingly simple calculation of LCM(2,3) = 6 opens the door to a deeper understanding of number theory and its numerous applications.
Latest Posts
Latest Posts
-
What Is 20 Of 700
Sep 23, 2025
-
Weight Of 1 Litre Water
Sep 23, 2025
-
How To Measure The Head
Sep 23, 2025
-
Venn Diagram For Independent Events
Sep 23, 2025
-
Will Sunburn Turn To Tan
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 2 And 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.