What Is 20 Of 700
dulhadulhi
Sep 23, 2025 · 5 min read
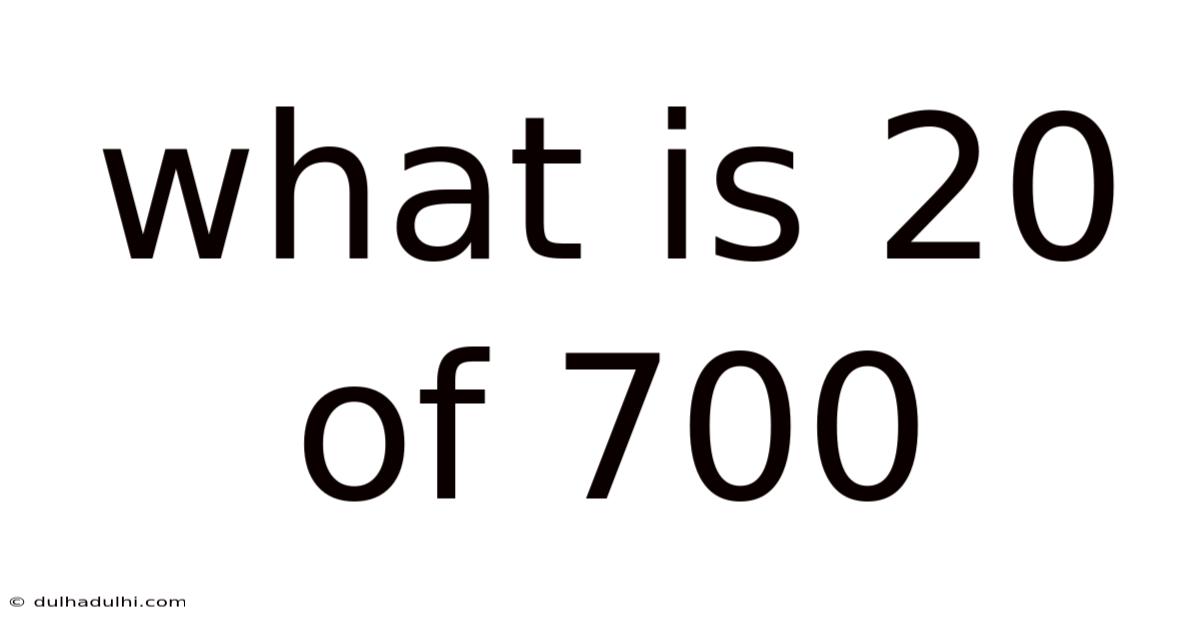
Table of Contents
What is 20 of 700? Understanding Percentages, Fractions, and Ratios
Finding out "what is 20 of 700?" might seem like a simple question, but it opens the door to understanding fundamental mathematical concepts like percentages, fractions, and ratios. This seemingly straightforward calculation has practical applications in many areas, from calculating discounts and sales tax to understanding statistical data and proportions in various fields. This article will delve deep into the solution, explaining the different methods to arrive at the answer and exploring the underlying mathematical principles involved.
Understanding the Problem: Percentages, Fractions, and Ratios
The question "What is 20 of 700?" is essentially asking us to determine what percentage or fraction 20 represents of the total amount 700. We can approach this using several different methods:
- Percentage: This expresses 20 as a proportion of 700, represented as a value out of 100.
- Fraction: This represents 20 as a part of the whole 700, expressed as a ratio of two numbers.
- Ratio: This compares the relationship between 20 and 700, showing their relative sizes.
Method 1: Calculating the Percentage
The most common way to interpret "20 of 700" is as a percentage. To calculate the percentage, we use the following formula:
(Part / Whole) * 100%
In our case:
Part = 20 Whole = 700
Therefore:
(20 / 700) * 100% = 0.02857 * 100% = 2.857%
Therefore, 20 is approximately 2.857% of 700. This means that if we divide 700 into 100 equal parts, 20 would represent roughly 2.857 of those parts.
Method 2: Expressing it as a Fraction
Alternatively, we can express the relationship between 20 and 700 as a fraction:
20/700
This fraction can be simplified by finding the greatest common divisor (GCD) of 20 and 700. The GCD of 20 and 700 is 20. Dividing both the numerator and denominator by 20, we get:
20/700 = 1/35
This simplified fraction, 1/35, shows that 20 represents one part out of 35 equal parts that make up 700. This fraction is an equivalent representation to the percentage calculated in Method 1.
Method 3: Understanding the Ratio
The ratio of 20 to 700 can be expressed as:
20:700
Similar to the fraction, this ratio can be simplified by dividing both numbers by their GCD (20):
20:700 = 1:35
This simplified ratio indicates that for every one unit of 20, there are 35 units of 700. This is another way of representing the same relationship between the two numbers.
Practical Applications: Real-World Examples
Understanding how to calculate percentages, fractions, and ratios is crucial in various real-world scenarios. Here are a few examples:
- Sales and Discounts: Imagine a store offering a discount of 20 out of a total price of 700. Using the methods above, we know this represents a 2.857% discount.
- Statistical Analysis: If a survey of 700 people shows 20 prefer a particular product, we can determine that approximately 2.857% of the surveyed population prefers that product.
- Financial Calculations: Calculating interest rates, profits, and losses often involves working with percentages and ratios.
- Proportions and Scaling: In construction, cooking, or other fields requiring scaling, understanding ratios is essential for maintaining proper proportions.
- Data Interpretation: Many fields like science, economics, and social sciences use ratios and percentages to interpret data and draw conclusions.
Further Exploration: Beyond the Basics
While the calculation of "20 of 700" is relatively straightforward, it provides a solid foundation for understanding more complex mathematical concepts. Building upon this understanding, we can explore:
- Compound Interest: Understanding percentages is fundamental to calculating compound interest, which is crucial for financial planning and investment strategies.
- Probability: Fractions and ratios are essential tools in probability theory, allowing us to calculate the likelihood of different events occurring.
- Statistical Significance: In statistical analysis, determining the significance of a result often involves comparing proportions and ratios.
- Advanced Algebra: The concepts of ratios and proportions form the basis for many algebraic equations and problem-solving techniques.
Frequently Asked Questions (FAQ)
Q: Can I use a calculator to solve this problem?
A: Yes, absolutely! A simple calculator can easily perform the division (20/700) and then the multiplication by 100% to find the percentage.
Q: Why is it important to simplify fractions and ratios?
A: Simplifying makes it easier to understand and visualize the relationship between the numbers. It provides a clearer representation of the proportion.
Q: What if the numbers were larger or more complex?
A: The same methods would apply. You would simply use the same formulas, potentially using a calculator for larger numbers.
Q: Are there any other ways to represent this relationship besides percentages, fractions, and ratios?
A: You could also use decimal representation (0.02857). Visual representations like pie charts or bar graphs could also help illustrate the relationship between 20 and 700.
Conclusion: Mastering the Fundamentals
The seemingly simple question, "What is 20 of 700?", reveals the importance of understanding fundamental mathematical concepts like percentages, fractions, and ratios. These concepts are not only crucial for solving mathematical problems but also for interpreting data, making informed decisions, and succeeding in various real-world applications. Mastering these basic concepts provides a strong foundation for tackling more advanced mathematical challenges and contributes to a broader understanding of the quantitative world around us. The ability to seamlessly convert between percentages, fractions, and ratios demonstrates a solid grasp of proportional reasoning, a critical skill in many fields of study and professional endeavors. By understanding the underlying principles, you're not just finding the answer to a single question; you're equipping yourself with a powerful set of tools for tackling a wide range of quantitative problems.
Latest Posts
Latest Posts
-
Solving One Step Equations Worksheet
Sep 23, 2025
-
Equation Of A Plane Vectors
Sep 23, 2025
-
Worksheet On Tens And Ones
Sep 23, 2025
-
How To Find Uncertainty Chemistry
Sep 23, 2025
-
How Tall Is 171 Cm
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about What Is 20 Of 700 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.