Lcm Of 4 And 10
dulhadulhi
Sep 23, 2025 · 6 min read
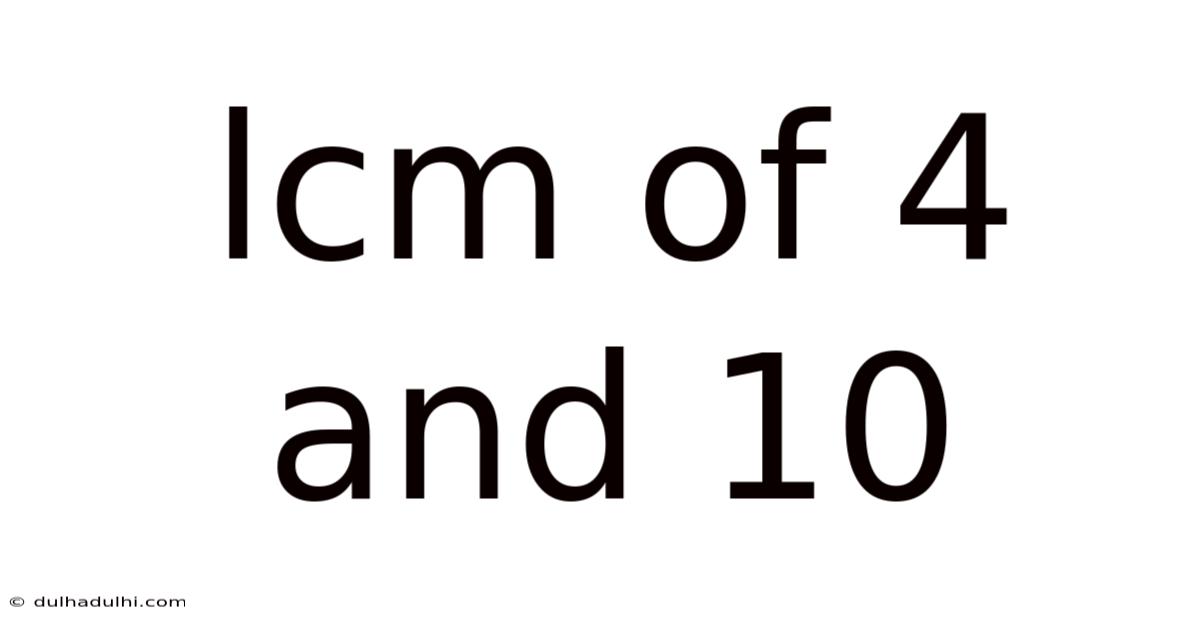
Table of Contents
Understanding the Least Common Multiple (LCM) of 4 and 10: A Comprehensive Guide
Finding the least common multiple (LCM) might seem like a simple mathematical task, especially for small numbers like 4 and 10. However, understanding the underlying concepts and different methods for calculating the LCM is crucial for grasping more advanced mathematical concepts. This article provides a detailed explanation of how to find the LCM of 4 and 10, explores various methods, and delves into the theoretical foundations behind this important concept. We'll cover everything from basic definitions to more advanced techniques, ensuring you develop a strong understanding of LCM calculations and their applications.
What is the Least Common Multiple (LCM)?
The Least Common Multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers. In simpler terms, it's the smallest number that contains all the numbers in your set as factors. Think of it as finding the smallest common "parking spot" for a set of numbers. For instance, if you have two cars (numbers), the LCM is the smallest sized parking spot that can fit both cars without any overlap.
Understanding LCM is fundamental to various mathematical operations, particularly in fractions, simplifying expressions, and solving problems related to cycles and patterns. It's a building block for more complex mathematical concepts encountered in higher-level studies.
Methods to Find the LCM of 4 and 10
There are several ways to determine the LCM of 4 and 10. Let's explore the most common methods:
1. Listing Multiples:
This is the most straightforward method, especially for smaller numbers. We list the multiples of each number until we find the smallest common multiple.
- Multiples of 4: 4, 8, 12, 16, 20, 24, 28, 32...
- Multiples of 10: 10, 20, 30, 40, 50...
By comparing the two lists, we can see that the smallest number present in both lists is 20. Therefore, the LCM of 4 and 10 is 20.
2. Prime Factorization Method:
This method involves finding the prime factorization of each number and then constructing the LCM from the prime factors.
- Prime factorization of 4: 2 x 2 = 2²
- Prime factorization of 10: 2 x 5
To find the LCM, we take the highest power of each prime factor present in either factorization:
- The highest power of 2 is 2² = 4
- The highest power of 5 is 5¹ = 5
Multiply these highest powers together: 4 x 5 = 20. Therefore, the LCM of 4 and 10 is 20. This method becomes particularly useful when dealing with larger numbers where listing multiples becomes cumbersome.
3. Using the Greatest Common Divisor (GCD):
The LCM and GCD (Greatest Common Divisor) of two numbers are related through a formula:
LCM(a, b) x GCD(a, b) = a x b
First, we need to find the GCD of 4 and 10. The GCD is the largest number that divides both 4 and 10 without leaving a remainder. In this case, the GCD(4, 10) = 2.
Now, we can use the formula:
LCM(4, 10) x GCD(4, 10) = 4 x 10 LCM(4, 10) x 2 = 40 LCM(4, 10) = 40 / 2 = 20
This method is efficient for larger numbers, especially when using the Euclidean algorithm to find the GCD.
4. Venn Diagram Method (Visual Representation):
While less commonly used for direct calculation, a Venn diagram can provide a helpful visual representation of the prime factors and their contribution to the LCM.
- Find the prime factorization of each number: 4 = 2 x 2 and 10 = 2 x 5.
- Draw two overlapping circles, one for each number's prime factorization.
- Place the common prime factor (2) in the overlapping region.
- Place the remaining prime factors (another 2 for 4 and 5 for 10) in the non-overlapping regions.
- Multiply all the prime factors in the diagram: 2 x 2 x 5 = 20. The LCM is 20.
Why is Understanding LCM Important?
The concept of LCM extends far beyond simple mathematical exercises. It has practical applications in various fields:
-
Scheduling and Timing: Determining when events will occur simultaneously. For example, if two machines have cycles of 4 and 10 minutes respectively, the LCM (20 minutes) represents when both will complete a cycle at the same time.
-
Fractions: Finding the least common denominator (LCD) when adding or subtracting fractions. The LCD is the LCM of the denominators. For example, to add 1/4 and 1/10, you'd need to find the LCM of 4 and 10 (which is 20) to create a common denominator.
-
Modular Arithmetic: Used in cryptography and other areas of mathematics where cyclical patterns are important.
-
Music Theory: Determining harmonic intervals and chord progressions.
-
Construction and Engineering: Coordinating projects where different parts of the work have various cycle times.
Deeper Dive: Mathematical Foundations of LCM
The calculation of the LCM relies on fundamental number theory concepts:
-
Divisibility: A number 'a' is divisible by a number 'b' if the remainder is 0 when 'a' is divided by 'b'.
-
Prime Numbers: A prime number is a natural number greater than 1 that is not a product of two smaller natural numbers. Prime factorization is the process of expressing a number as a product of its prime factors. The fundamental theorem of arithmetic states that every integer greater than 1 can be represented uniquely as a product of prime numbers. This uniqueness is critical in calculating the LCM using prime factorization.
-
Euclidean Algorithm: An efficient algorithm for finding the greatest common divisor (GCD) of two integers. The GCD is intrinsically linked to the LCM through the formula mentioned earlier. The Euclidean algorithm is particularly useful when dealing with larger numbers, making the GCD calculation significantly faster than other methods.
Frequently Asked Questions (FAQ)
Q: What if I have more than two numbers? How do I find the LCM?
A: You can extend the methods described above to find the LCM of more than two numbers. For prime factorization, you'd consider all prime factors from all numbers and take the highest power of each. For the listing method, you'd need to list multiples of all numbers until you find the smallest common multiple.
Q: Is there a formula for calculating the LCM of any two numbers?
A: Yes, the formula relating the LCM and GCD is a general formula: LCM(a, b) = (a * b) / GCD(a, b)
Q: Why is the LCM important in adding fractions?
A: To add fractions, you need a common denominator. The least common denominator (LCD) is the LCM of the denominators. Using the LCD ensures that you are working with the smallest possible common denominator, simplifying calculations.
Q: Can the LCM of two numbers be larger than both numbers?
A: Yes, in most cases the LCM will be larger than or equal to both numbers. The only exception is when the two numbers are equal, in which case the LCM is equal to both numbers.
Conclusion
Finding the LCM of 4 and 10, while seemingly simple, serves as a gateway to understanding a broader range of mathematical concepts. Mastering various methods for calculating LCM, such as listing multiples, prime factorization, and using the GCD, builds a solid foundation for tackling more complex problems in arithmetic, algebra, and beyond. The practical applications of LCM extend beyond theoretical mathematics, finding utility in scheduling, fractions, modular arithmetic, and various other fields. Understanding the underlying principles of LCM and GCD provides a significant advantage in tackling mathematical challenges and solving real-world problems efficiently. By grasping these fundamental concepts, you equip yourself with a powerful tool for problem-solving across numerous disciplines.
Latest Posts
Latest Posts
-
7 4 As A Decimal
Sep 23, 2025
-
L C M Of 10 And 12
Sep 23, 2025
-
Uses Of Glucose In Plants
Sep 23, 2025
-
What Is 121 Square Root
Sep 23, 2025
-
Series And Parallel Circuits Capacitors
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 4 And 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.