What Is 121 Square Root
dulhadulhi
Sep 23, 2025 · 5 min read
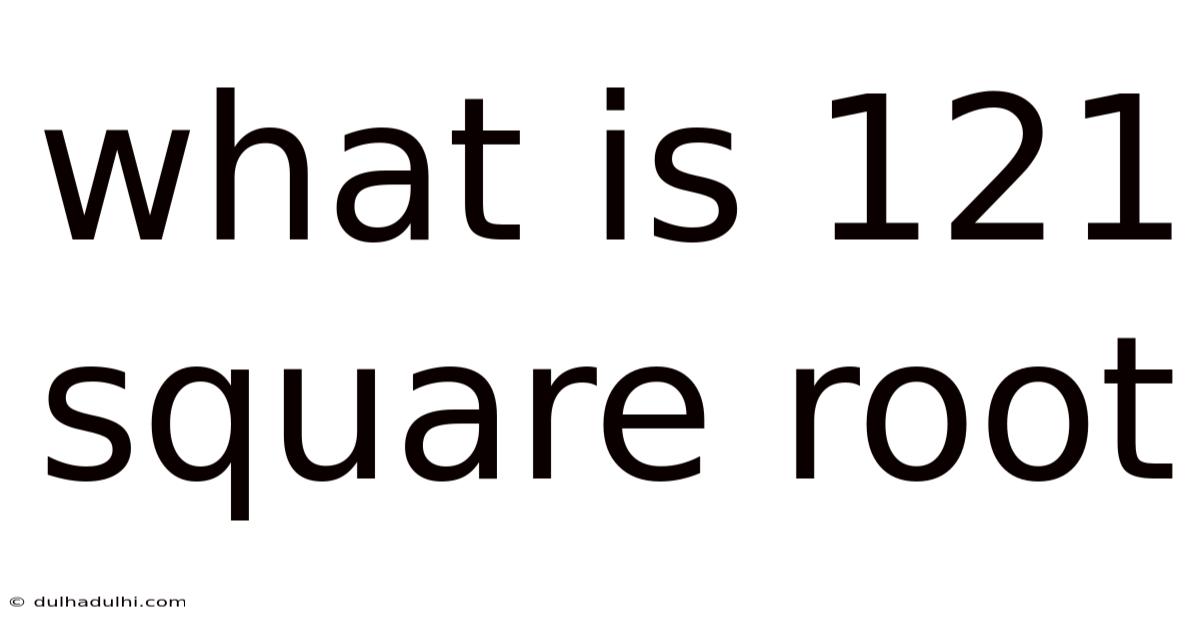
Table of Contents
What is the Square Root of 121? A Comprehensive Exploration
Understanding square roots is fundamental in mathematics, forming the bedrock for more advanced concepts. This article delves into the square root of 121, exploring not just the answer but also the underlying principles, methods for calculating square roots, and its applications in various fields. We'll cover everything from basic definitions to more advanced techniques, ensuring a comprehensive understanding for learners of all levels. This exploration will also touch upon related mathematical concepts to provide a richer, more holistic understanding.
What is a Square Root?
Before diving into the square root of 121, let's establish a clear understanding of what a square root actually is. A square root of a number is a value that, when multiplied by itself (squared), gives the original number. For example, the square root of 9 is 3 because 3 multiplied by itself (3 x 3 = 9) equals 9. It's essentially the inverse operation of squaring a number.
Symbolically, the square root is represented by the radical symbol (√). So, the square root of 121 is written as √121.
Calculating the Square Root of 121: The Simple Approach
For smaller numbers like 121, finding the square root can be done through simple observation and memorization of perfect squares. A perfect square is a number that can be obtained by squaring an integer. By listing out the squares of integers, we can quickly identify the square root of 121:
1 x 1 = 1 2 x 2 = 4 3 x 3 = 9 4 x 4 = 16 5 x 5 = 25 6 x 6 = 36 7 x 7 = 49 8 x 8 = 64 9 x 9 = 81 10 x 10 = 100 11 x 11 = 121 12 x 12 = 144
As we can see from the list above, 11 multiplied by itself (11 x 11) equals 121. Therefore, the square root of 121 is 11.
Understanding Positive and Negative Square Roots
It's crucial to remember that every positive number has two square roots: one positive and one negative. While we commonly focus on the principal square root (the positive one), it's important to acknowledge the existence of the negative counterpart. In the case of 121, the square roots are +11 and -11, because both (11 x 11) and (-11 x -11) equal 121.
However, when you see the √ symbol, it usually implies the principal square root (the positive one), unless otherwise specified.
Methods for Calculating Square Roots of Larger Numbers
While the simple method works well for smaller perfect squares, it becomes impractical for larger numbers. Several methods exist for calculating square roots of larger numbers, including:
-
Prime Factorization: This method involves breaking down the number into its prime factors. Once you have the prime factorization, you can find the square root by pairing up the prime factors. For example, finding the square root of 36 (2 x 2 x 3 x 3) is straightforward after pairing up the 2s and the 3s. This method is particularly useful for perfect squares.
-
Babylonian Method (or Heron's Method): This iterative method provides an approximation of the square root. It involves starting with an initial guess and repeatedly refining it using a specific formula until the desired level of accuracy is reached. This method is highly efficient for larger numbers and forms the basis of many numerical algorithms used in computers.
-
Using a Calculator: Modern calculators have built-in functions to calculate square roots directly, providing a quick and accurate solution, especially for non-perfect squares.
-
Long Division Method: This is a more manual method, often taught in schools, that involves a series of steps to approximate the square root. While it's less common now with the prevalence of calculators, it provides a deeper understanding of the underlying calculation.
The Square Root of 121 in Different Mathematical Contexts
The square root of 121, being a simple and straightforward example, is used extensively in various mathematical contexts, including:
-
Geometry: It's frequently encountered in geometric calculations involving squares, rectangles, and other shapes. For example, finding the side length of a square with an area of 121 square units involves calculating the square root of 121 (which is 11 units).
-
Algebra: Square roots are fundamental to solving quadratic equations, which are equations of the form ax² + bx + c = 0. These equations often involve taking the square root to find the solutions for 'x'.
-
Trigonometry: Square roots appear in trigonometric identities and formulas, contributing to the calculation of angles and lengths within triangles.
-
Calculus: Square roots appear extensively in many calculus concepts, such as finding derivatives and integrals of functions involving square roots.
-
Physics and Engineering: In physics and engineering, square roots are frequently used in calculations involving velocity, acceleration, energy, and many other quantities.
Frequently Asked Questions (FAQ)
Q1: Is the square root of 121 always 11?
A1: When referring to the principal square root, yes, it's always 11. However, there's also a negative square root, -11, because (-11) x (-11) = 121.
Q2: How can I calculate the square root of a number that isn't a perfect square?
A2: For non-perfect squares, you can use the Babylonian method (iterative approximation), a calculator, or the long division method for an approximate value.
Q3: What are some real-world applications of square roots?
A3: Square roots are used in various fields like engineering (calculating distances and forces), physics (solving equations related to motion and energy), and computer graphics (working with coordinate systems and transformations).
Q4: What happens if I try to take the square root of a negative number?
A4: Taking the square root of a negative number results in an imaginary number. Imaginary numbers are represented using the imaginary unit 'i', where i² = -1. For instance, the square root of -1 is 'i'.
Conclusion: The Significance of Understanding Square Roots
The square root of 121, seemingly a simple calculation, serves as a gateway to understanding a crucial mathematical concept with far-reaching implications. Mastering square roots is essential for progressing in mathematics and its numerous applications in other scientific and engineering fields. This exploration has covered the basic definition, calculation methods, and the significance of square roots in various contexts. By understanding these fundamentals, you’ll be better equipped to tackle more complex mathematical challenges in the future. Remember to practice regularly, explore different methods of calculation, and don't hesitate to delve deeper into the fascinating world of numbers and their relationships.
Latest Posts
Latest Posts
-
Convert Litres To Uk Gallons
Sep 23, 2025
-
Words With The Soft C
Sep 23, 2025
-
Do Fish Grow Back Fins
Sep 23, 2025
-
How Much Is 10 Gm
Sep 23, 2025
-
Calcium Carbonate Hydrochloric Acid
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about What Is 121 Square Root . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.