Gcf Of 24 And 56
dulhadulhi
Sep 22, 2025 · 6 min read
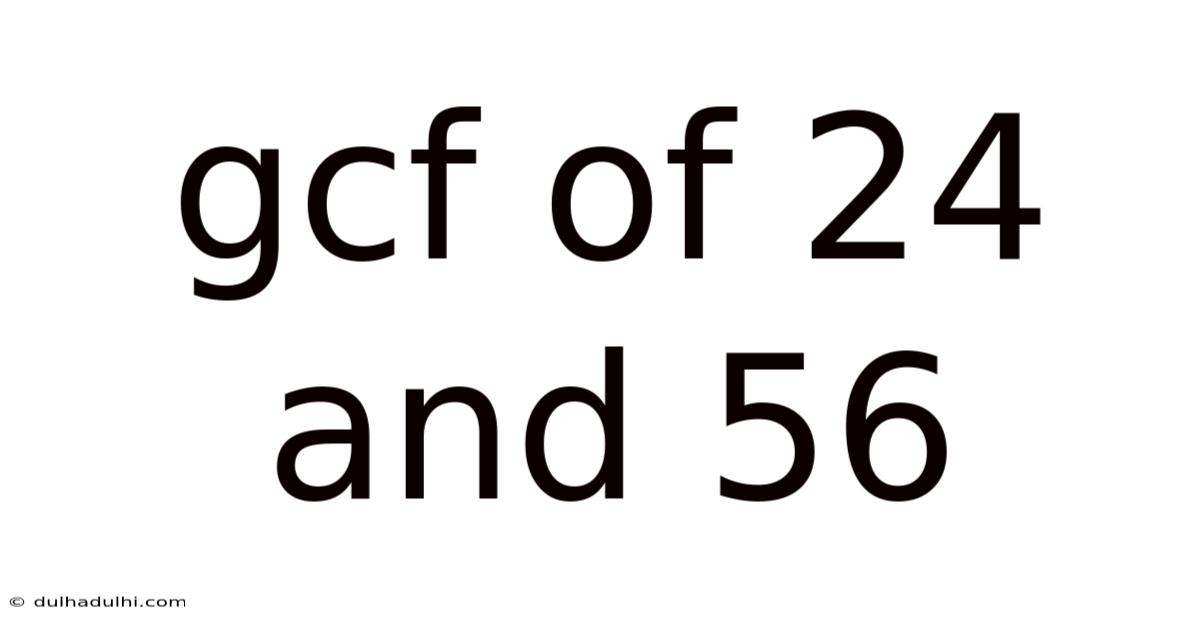
Table of Contents
Unveiling the Greatest Common Factor (GCF) of 24 and 56: A Deep Dive
Finding the greatest common factor (GCF), also known as the greatest common divisor (GCD), of two numbers might seem like a simple arithmetic task. However, understanding the underlying principles and various methods for calculating the GCF opens up a world of mathematical understanding, extending far beyond basic number theory. This article will explore the GCF of 24 and 56 in detail, using different approaches to illustrate the concepts and provide a comprehensive understanding of this fundamental mathematical concept. We will delve into the prime factorization method, the Euclidean algorithm, and even explore the visual representation using Venn diagrams. By the end, you'll not only know the GCF of 24 and 56 but also possess a deeper understanding of this essential concept applicable in various mathematical fields.
Understanding the Greatest Common Factor (GCF)
Before diving into the calculation, let's solidify our understanding of the GCF. The GCF of two or more integers is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that can perfectly divide both numbers. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12. The factors of 18 are 1, 2, 3, 6, 9, and 18. The common factors of 12 and 18 are 1, 2, 3, and 6. The greatest common factor is 6.
This concept is crucial in various mathematical applications, including simplifying fractions, solving algebraic equations, and understanding number relationships. Finding the GCF is a fundamental skill for anyone studying mathematics, from elementary school to advanced levels.
Method 1: Prime Factorization
The prime factorization method involves breaking down each number into its prime factors—numbers divisible only by 1 and themselves. Then, we identify the common prime factors and multiply them together to find the GCF.
Let's apply this method to find the GCF of 24 and 56:
1. Prime Factorization of 24:
We can express 24 as a product of its prime factors:
24 = 2 x 2 x 2 x 3 = 2³ x 3
2. Prime Factorization of 56:
Similarly, we find the prime factorization of 56:
56 = 2 x 2 x 2 x 7 = 2³ x 7
3. Identifying Common Factors:
Now, we compare the prime factorizations of 24 and 56:
24 = 2³ x 3 56 = 2³ x 7
The common prime factor is 2, and it appears three times in both factorizations (2³).
4. Calculating the GCF:
To find the GCF, we multiply the common prime factors:
GCF(24, 56) = 2³ = 8
Therefore, the greatest common factor of 24 and 56 is 8.
Method 2: The Euclidean Algorithm
The Euclidean algorithm provides a more efficient method, especially when dealing with larger numbers. This algorithm relies on repeated division with remainders. The steps are as follows:
1. Divide the larger number by the smaller number:
Divide 56 by 24:
56 ÷ 24 = 2 with a remainder of 8 (56 = 24 x 2 + 8)
2. Replace the larger number with the smaller number, and the smaller number with the remainder:
Now we have 24 and 8.
3. Repeat the process:
Divide 24 by 8:
24 ÷ 8 = 3 with a remainder of 0
4. The GCF is the last non-zero remainder:
Since the remainder is 0, the GCF is the previous remainder, which is 8.
Therefore, the Euclidean algorithm confirms that the GCF of 24 and 56 is 8.
Method 3: Listing Factors
While less efficient for larger numbers, listing factors can be a helpful visualization method, especially for beginners.
1. List the factors of 24:
1, 2, 3, 4, 6, 8, 12, 24
2. List the factors of 56:
1, 2, 4, 7, 8, 14, 28, 56
3. Identify common factors:
The common factors are 1, 2, 4, and 8.
4. Determine the greatest common factor:
The greatest common factor among these is 8.
Visual Representation: Venn Diagrams
Venn diagrams can provide a visual representation of the factors and help in understanding the concept of GCF. We can represent the factors of 24 and 56 in separate circles, with the overlapping area representing the common factors.
[Imagine a Venn diagram here with two overlapping circles. One circle labeled "Factors of 24" containing 1, 2, 3, 4, 6, 8, 12, 24. The other circle labeled "Factors of 56" containing 1, 2, 4, 7, 8, 14, 28, 56. The overlapping area contains 1, 2, 4, 8.]
The overlapping section (the intersection) shows the common factors: 1, 2, 4, and 8. The largest number in the intersection is 8, confirming that the GCF of 24 and 56 is 8.
Applications of GCF
The GCF has numerous applications in various mathematical and real-world contexts:
-
Simplifying Fractions: To simplify a fraction, we divide both the numerator and denominator by their GCF. For example, the fraction 24/56 can be simplified to 3/7 by dividing both by their GCF, which is 8.
-
Solving Algebraic Equations: Finding the GCF is essential in factoring polynomials, a crucial step in solving many algebraic equations.
-
Geometry and Measurement: GCF helps in solving problems related to area, perimeter, and volume, where we need to find the largest common divisor of given measurements.
-
Number Theory: GCF forms the basis for understanding many concepts in number theory, such as modular arithmetic and the least common multiple (LCM). The LCM and GCF are closely related; their product equals the product of the original numbers. In our case, LCM(24,56) * GCF(24,56) = 24 * 56. Knowing one allows the easy calculation of the other.
-
Real-world applications: Imagine you have 24 apples and 56 oranges, and you want to divide them into identical bags with the maximum number of fruits in each bag. The GCF (8) tells you that you can create 8 bags, each containing 3 apples and 7 oranges.
Frequently Asked Questions (FAQ)
Q: What if the GCF is 1?
A: If the GCF of two numbers is 1, it means they are relatively prime or coprime. This indicates that they share no common factors other than 1.
Q: Can the GCF be negative?
A: While the factors themselves can be negative, the GCF is always defined as the largest positive integer.
Q: How do I find the GCF of more than two numbers?
A: You can extend the methods discussed above. For example, using prime factorization, you would find the prime factorization of each number, and then identify the common prime factors with the lowest exponent. For the Euclidean algorithm, you would repeatedly find the GCF of pairs of numbers until you're left with the GCF of all the numbers.
Q: Are there any limitations to these methods?
A: The prime factorization method can be time-consuming for very large numbers. The Euclidean algorithm is generally more efficient for larger numbers. The listing factors method is impractical for large numbers.
Conclusion
Finding the greatest common factor of 24 and 56, which we've determined to be 8, is not merely an exercise in arithmetic. It's a stepping stone to understanding fundamental mathematical concepts with wide-ranging applications. Whether using prime factorization, the Euclidean algorithm, or even visual aids like Venn diagrams, understanding the GCF allows us to simplify problems, solve equations, and gain a deeper appreciation for the intricate relationships between numbers. The methods presented here provide a solid foundation for tackling more complex mathematical challenges in the future. The key is to understand the underlying principles and select the most appropriate method depending on the specific numbers involved. Remember, mastering the GCF is not just about getting the right answer; it’s about understanding the process and its implications within the broader world of mathematics.
Latest Posts
Latest Posts
-
Black Light And Uv Light
Sep 22, 2025
-
Hcf Of 9 And 18
Sep 22, 2025
-
What Is 5 Of 400000
Sep 22, 2025
-
Is 1 2 Greater Than 3 4
Sep 22, 2025
-
4 X 6 In Cm
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about Gcf Of 24 And 56 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.