Is 1/2 Greater Than 3/4
dulhadulhi
Sep 22, 2025 · 5 min read
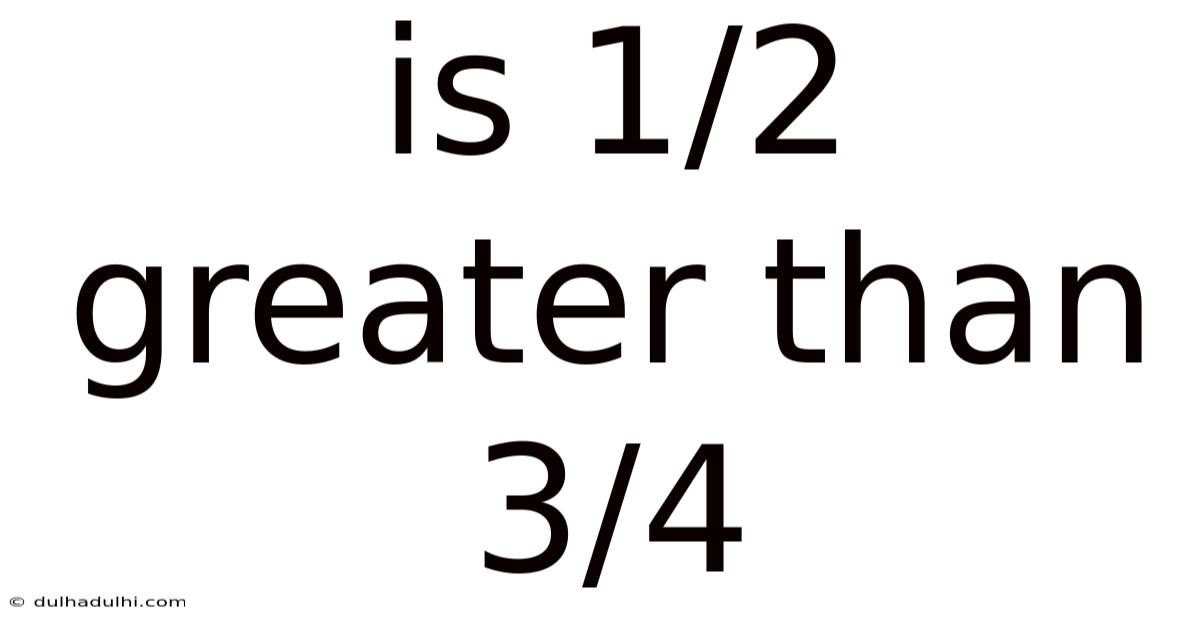
Table of Contents
Is 1/2 Greater Than 3/4? Understanding Fractions and Comparisons
Is 1/2 greater than 3/4? This seemingly simple question actually opens the door to a deeper understanding of fractions, a fundamental concept in mathematics. The answer, of course, is no, but the why behind the answer is crucial for developing strong mathematical reasoning skills. This article will explore the comparison of fractions, providing a comprehensive explanation suitable for learners of all levels, including a look at different methods for comparing fractions, and addressing common misconceptions.
Understanding Fractions: A Quick Refresher
Before diving into the comparison of 1/2 and 3/4, let's revisit the basics of fractions. A fraction represents a part of a whole. It consists of two parts:
- Numerator: The top number, indicating how many parts we have.
- Denominator: The bottom number, indicating the total number of equal parts the whole is divided into.
For instance, in the fraction 1/2, the numerator is 1 and the denominator is 2. This means we have 1 out of 2 equal parts of a whole. Similarly, 3/4 means we have 3 out of 4 equal parts.
Visualizing the Comparison: The Power of Pictorial Representation
One of the most effective ways to understand fraction comparisons is through visualization. Let's imagine two identical pizzas.
- Pizza 1: We cut this pizza into two equal halves. We take one of these halves (1/2).
- Pizza 2: We cut this pizza into four equal quarters. We take three of these quarters (3/4).
By looking at the two pizzas, it becomes immediately apparent that three-quarters of a pizza (3/4) is larger than one-half (1/2). This visual representation helps to solidify the understanding that 1/2 is not greater than 3/4.
Method 1: Finding a Common Denominator
A more formal, mathematical approach involves finding a common denominator. This is a crucial technique for comparing fractions with different denominators. The common denominator is a number that is a multiple of both denominators. In our case, we have 1/2 and 3/4. The denominators are 2 and 4. A common denominator is 4 (because 4 is a multiple of 2).
Now, we need to rewrite the fractions with the common denominator of 4:
- 1/2: To change the denominator from 2 to 4, we multiply both the numerator and the denominator by 2: (1 x 2) / (2 x 2) = 2/4
- 3/4: This fraction already has a denominator of 4, so it remains unchanged.
Now we can easily compare 2/4 and 3/4. Since 2 is less than 3, we conclude that 2/4 (which is equivalent to 1/2) is less than 3/4.
Method 2: Converting to Decimals
Another way to compare fractions is to convert them into decimals. This involves dividing the numerator by the denominator.
- 1/2: 1 ÷ 2 = 0.5
- 3/4: 3 ÷ 4 = 0.75
Comparing 0.5 and 0.75, it's clear that 0.75 (3/4) is greater than 0.5 (1/2). This method is particularly helpful when dealing with fractions that are difficult to visualize or to find a common denominator for.
Method 3: Using Cross-Multiplication
Cross-multiplication provides a straightforward method for comparing two fractions. This method is particularly useful when finding a common denominator is cumbersome.
To compare 1/2 and 3/4 using cross-multiplication:
- Multiply the numerator of the first fraction (1) by the denominator of the second fraction (4): 1 x 4 = 4
- Multiply the numerator of the second fraction (3) by the denominator of the first fraction (2): 3 x 2 = 6
Compare the results: 4 < 6. Since 4 is less than 6, the fraction 1/2 (which was used in the first multiplication) is smaller than 3/4.
Addressing Common Misconceptions
Several misconceptions can hinder the understanding of fraction comparison:
- Focusing solely on numerators: Students sometimes mistakenly believe that because 3 (the numerator of 3/4) is greater than 1 (the numerator of 1/2), 3/4 must be greater. This ignores the crucial role of the denominator.
- Incorrect use of common denominators: Errors can occur when finding a common denominator or when incorrectly converting fractions to equivalent forms.
- Ignoring the whole: Remembering that fractions represent parts of a whole is crucial. Comparing fractions without considering the whole can lead to incorrect conclusions.
Why is Understanding Fraction Comparison Important?
Understanding fraction comparison is vital for various reasons:
- Foundation for advanced math: It forms the basis for understanding more complex mathematical concepts like ratios, proportions, and percentages.
- Real-world applications: Comparing fractions is essential in everyday situations, such as measuring ingredients in recipes, calculating discounts, and understanding data representation.
- Problem-solving skills: Mastering fraction comparison enhances problem-solving skills and logical reasoning abilities.
Frequently Asked Questions (FAQ)
Q1: What if I have fractions with different denominators and I can't easily find a common denominator?
A1: In such cases, converting to decimals or using cross-multiplication is a more efficient approach.
Q2: Can I always use cross-multiplication to compare fractions?
A2: Yes, cross-multiplication provides a reliable method for comparing any two fractions.
Q3: Are there other visual methods to compare fractions besides using pizzas?
A3: Yes, you can use fraction bars, number lines, or other visual aids to represent and compare fractions.
Conclusion
In conclusion, 1/2 is not greater than 3/4. This article has explored several methods – visualization, finding a common denominator, converting to decimals, and cross-multiplication – to effectively compare fractions. Understanding these methods and avoiding common misconceptions is key to mastering fraction comparison and building a strong foundation in mathematics. Remember, the key to success lies in understanding the underlying concepts and employing the most appropriate method for the given problem. By consistently practicing and applying these techniques, you will confidently navigate the world of fractions and their comparisons.
Latest Posts
Latest Posts
-
What Is 4cm In Mm
Sep 22, 2025
-
Physics And Math Tutor Biology
Sep 22, 2025
-
Regular And Non Regular Polygons
Sep 22, 2025
-
8 Out Of 11 Percentage
Sep 22, 2025
-
First 5 Multiples Of 6
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about Is 1/2 Greater Than 3/4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.