Cos 2 Sin 2 1
dulhadulhi
Sep 24, 2025 · 5 min read
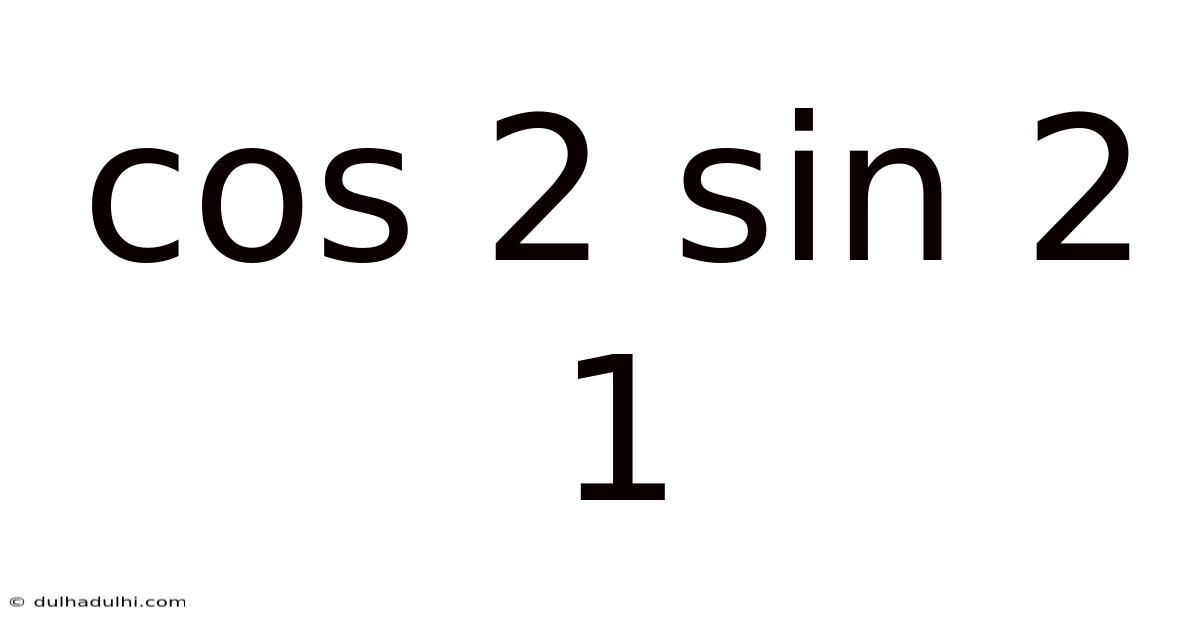
Table of Contents
Decoding cos²x - sin²x = 1: A Deep Dive into Trigonometric Identities
This article explores the trigonometric identity cos²x - sin²x = 1, clarifying its meaning, derivation, and applications. While the equation as stated is incorrect (the correct identity is cos²x + sin²x = 1), we will dissect the fundamental Pythagorean identity and explore related concepts to provide a comprehensive understanding of trigonometric relationships. We will also address common misconceptions and answer frequently asked questions. This in-depth exploration will equip you with a strong foundational understanding of trigonometry.
Introduction: The Pythagorean Identity and its Significance
The core of trigonometry rests upon fundamental identities, relationships that hold true for all angles. The most important of these is the Pythagorean identity: cos²x + sin²x = 1. This identity is derived directly from the Pythagorean theorem applied to a right-angled triangle. Understanding this identity is crucial for simplifying trigonometric expressions, solving equations, and proving other trigonometric identities. It forms the bedrock of numerous applications in calculus, physics, engineering, and other fields. It's essential to note that cos²x - sin²x ≠ 1; this is a common error. The correct relationship, as we'll explore, is derived from the fundamental cos²x + sin²x = 1.
Deriving the Pythagorean Identity: A Geometric Approach
Consider a right-angled triangle with hypotenuse of length 1. Let x be one of the acute angles. The side adjacent to x has length cos x, and the side opposite x has length sin x. Applying the Pythagorean theorem (a² + b² = c²), we get:
(cos x)² + (sin x)² = 1²
This simplifies to:
cos²x + sin²x = 1
This geometric derivation beautifully illustrates the inherent connection between the Pythagorean theorem and the fundamental trigonometric identity. This identity holds true regardless of the value of x, whether it's an acute, obtuse, or reflex angle. The beauty of trigonometry lies in its ability to extend these geometric concepts to angles beyond the confines of a right-angled triangle.
Understanding the Double Angle Identities and their Connection
The Pythagorean identity is the key to deriving several other important trigonometric identities, including the double-angle formulas. Let's explore how:
-
cos(2x): We can express cos(2x) in three equivalent ways using the Pythagorean identity:
- cos(2x) = cos²x - sin²x
- cos(2x) = 2cos²x - 1
- cos(2x) = 1 - 2sin²x
These different forms are incredibly useful depending on the context of a problem. For instance, if you have an expression involving only cos x, the second form is more convenient. If you have an expression involving only sin x, the third form is preferable.
-
sin(2x): The double angle identity for sin(2x) is derived from the sum-to-product formula, but it’s also closely related to the Pythagorean identity through its derivation:
- sin(2x) = 2sin x cos x
This identity, too, is fundamental in various applications, allowing for simplification of expressions and solutions to trigonometric equations.
Applications of the Pythagorean Identity and Double Angle Formulas
The applications of cos²x + sin²x = 1 and its derived identities are vast and span multiple disciplines:
-
Simplifying Trigonometric Expressions: The Pythagorean identity is invaluable in simplifying complex trigonometric expressions. By replacing terms like sin²x with 1 - cos²x or vice versa, you can significantly reduce the complexity of an expression, often making it solvable.
-
Solving Trigonometric Equations: The identities allow us to rewrite equations into simpler, more manageable forms. This can lead to finding solutions for x that might otherwise be difficult to obtain directly.
-
Calculus: In calculus, the Pythagorean identity and related double-angle formulas are frequently used in integration and differentiation problems involving trigonometric functions. It allows for simplification of integrals that might appear daunting initially.
-
Physics and Engineering: Many physical phenomena, such as oscillations and waves, are described using trigonometric functions. The identities are essential tools for analyzing these phenomena and solving related problems. Applications range from analyzing simple harmonic motion to modeling wave propagation.
-
Computer Graphics and Game Development: Trigonometric identities are crucial in computer graphics and game development for representing rotations, transformations, and other geometric operations. They are essential for creating realistic and dynamic visuals.
Addressing Common Misconceptions
A common error is to confuse cos²x - sin²x with the Pythagorean identity. It's crucial to remember that:
-
cos²x + sin²x = 1 is the fundamental Pythagorean identity.
-
cos²x - sin²x = cos(2x) is a derived double-angle formula, not an independent identity equal to 1.
Understanding this distinction is key to accurate trigonometric calculations and problem-solving.
Frequently Asked Questions (FAQ)
-
Q: Why is the Pythagorean identity so important?
A: The Pythagorean identity is fundamental because it connects the sine and cosine functions, providing a relationship that holds true for any angle. This relationship is crucial for simplifying expressions, solving equations, and forming the basis for many other trigonometric identities.
-
Q: How can I remember the Pythagorean identity?
A: The best way to remember it is through its geometric derivation. Visualizing the right-angled triangle and applying the Pythagorean theorem helps solidify the understanding.
-
Q: Are there any other important trigonometric identities?
A: Yes, many other important identities exist, including sum-to-product formulas, product-to-sum formulas, and identities involving tangent, cotangent, secant, and cosecant functions. These are often derived from the fundamental Pythagorean identity.
-
Q: How can I improve my understanding of trigonometry?
A: Practice is crucial. Work through numerous problems, starting with simpler ones and gradually progressing to more complex ones. Understanding the geometric interpretations helps to build intuition.
Conclusion: Mastering Trigonometric Identities
The Pythagorean identity, cos²x + sin²x = 1, is a cornerstone of trigonometry. Its applications are widespread, impacting various fields from mathematics and physics to computer science and engineering. By grasping its derivation, understanding its relationship to double-angle formulas, and addressing common misconceptions, you gain a solid foundation for further exploration in trigonometry and its numerous applications. The journey of mastering trigonometric identities is a rewarding one, opening doors to a deeper appreciation of mathematics and its power in understanding the world around us. Remember that consistent practice and a strong understanding of the fundamental concepts are key to success in this fascinating area of mathematics.
Latest Posts
Latest Posts
-
Lcm Of 4 And 8
Sep 24, 2025
-
Sigma And Pi Bonds Difference
Sep 24, 2025
-
What Is 1 Of 10
Sep 24, 2025
-
Formula For Price Per Unit
Sep 24, 2025
-
3 8 Of An Inch
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about Cos 2 Sin 2 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.