Lcm Of 4 And 8
dulhadulhi
Sep 24, 2025 · 7 min read
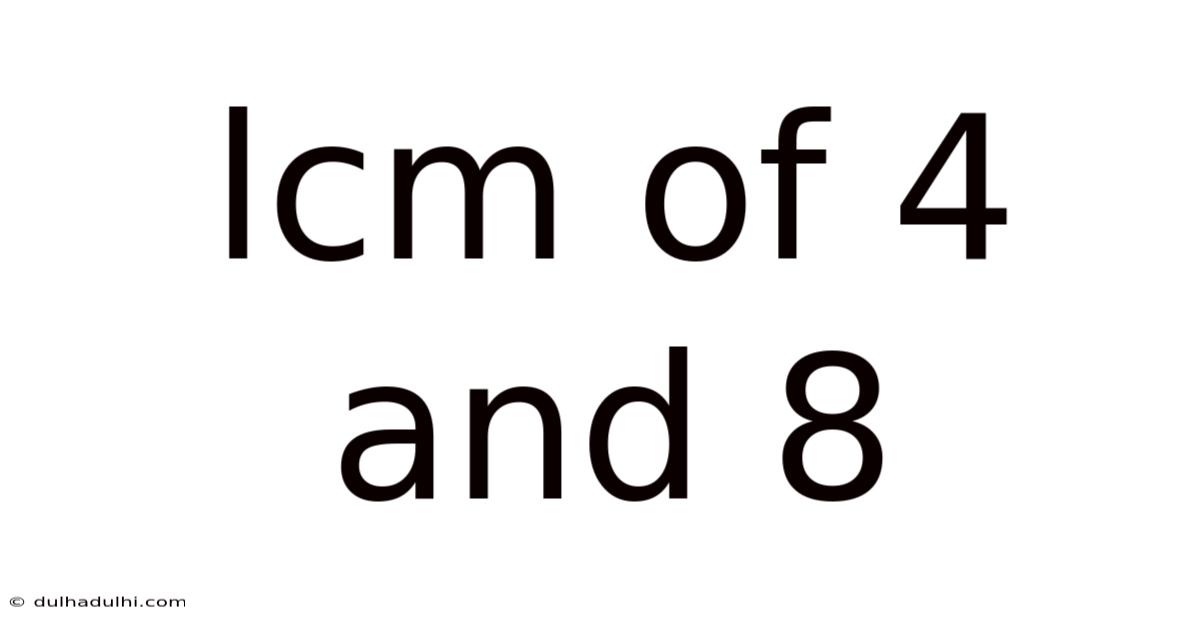
Table of Contents
Understanding the Least Common Multiple (LCM) of 4 and 8: A Deep Dive
Finding the least common multiple (LCM) of two numbers might seem like a simple arithmetic task, but understanding the underlying concepts unlocks a deeper appreciation of number theory and its applications in various fields. This article will thoroughly explore the LCM of 4 and 8, not just providing the answer but also explaining the different methods to calculate it, its significance in mathematics, and its practical relevance in real-world scenarios. We will delve into the theoretical underpinnings and illustrate the concepts with clear examples, making this a comprehensive guide for learners of all levels.
What is the Least Common Multiple (LCM)?
Before we jump into calculating the LCM of 4 and 8, let's define what the least common multiple actually is. The LCM of two or more integers is the smallest positive integer that is a multiple of all the numbers. In simpler terms, it's the smallest number that can be divided evenly by all the given numbers without leaving a remainder. Understanding multiples is crucial here. A multiple of a number is the result of multiplying that number by any whole number (0, 1, 2, 3, and so on).
For example, multiples of 4 are 0, 4, 8, 12, 16, 20, and so on. Multiples of 8 are 0, 8, 16, 24, 32, and so on. The LCM is the smallest positive number that appears in both lists.
Methods for Calculating the LCM of 4 and 8
There are several ways to calculate the LCM, each with its own advantages and disadvantages. Let's explore the most common methods:
1. Listing Multiples:
This is the most straightforward method, especially for smaller numbers like 4 and 8. We simply list the multiples of each number until we find the smallest common multiple.
- Multiples of 4: 4, 8, 12, 16, 20, 24...
- Multiples of 8: 8, 16, 24, 32...
By comparing the lists, we see that the smallest positive number that appears in both lists is 8. Therefore, the LCM(4, 8) = 8.
2. Prime Factorization Method:
This method is more efficient for larger numbers and provides a deeper understanding of the mathematical principles involved. It involves finding the prime factorization of each number. Prime factorization is expressing a number as a product of its prime factors (numbers divisible only by 1 and themselves).
- Prime factorization of 4: 2 x 2 = 2²
- Prime factorization of 8: 2 x 2 x 2 = 2³
To find the LCM using prime factorization, we take the highest power of each prime factor present in the factorizations and multiply them together. In this case, the highest power of 2 is 2³, so LCM(4, 8) = 2³ = 8.
3. Greatest Common Divisor (GCD) Method:
This method utilizes the relationship between the LCM and the greatest common divisor (GCD) of two numbers. The GCD is the largest number that divides both numbers without leaving a remainder. The relationship is given by the formula:
LCM(a, b) x GCD(a, b) = a x b
First, we find the GCD of 4 and 8. The divisors of 4 are 1, 2, and 4. The divisors of 8 are 1, 2, 4, and 8. The greatest common divisor is 4.
Now, we can use the formula:
LCM(4, 8) x GCD(4, 8) = 4 x 8 LCM(4, 8) x 4 = 32 LCM(4, 8) = 32 / 4 = 8
This confirms our previous results.
The Significance of LCM in Mathematics and Beyond
The concept of LCM is fundamental in various areas of mathematics and has practical applications in real-world scenarios:
-
Fraction Arithmetic: Finding a common denominator when adding or subtracting fractions requires finding the LCM of the denominators. For example, to add 1/4 and 3/8, we need to find the LCM of 4 and 8, which is 8. We then rewrite the fractions with a common denominator of 8: (2/8) + (3/8) = 5/8.
-
Scheduling and Time Management: The LCM is crucial in solving problems related to cyclical events. Imagine two machines that run on different cycles. One machine completes a cycle every 4 hours, and another every 8 hours. The LCM (8 hours) determines when both machines will complete a cycle simultaneously. This concept is applicable in various scheduling scenarios, such as coordinating shifts or planning events.
-
Modular Arithmetic: In modular arithmetic (a system of arithmetic for integers, where numbers "wrap around" upon reaching a certain value—the modulus), the LCM plays a role in determining the period of repeating patterns.
-
Number Theory: LCM is a key concept in number theory, a branch of mathematics that deals with the properties of integers. It's involved in proving various theorems and solving number-theoretic problems.
-
Geometry and Measurement: LCM is used in problems involving geometric figures with differing lengths or areas. For instance, finding the smallest length of a square tile needed to cover a rectangular floor of specific dimensions.
-
Music Theory: In music, the LCM helps determine the least common period of different musical rhythms or time signatures.
Visualizing the LCM: A Geometric Approach
We can visualize the LCM using geometric representations. Imagine you have two types of tiles: one with sides of length 4 units and another with sides of length 8 units. If you want to create a square using these tiles without cutting any of them, the side length of the square must be a multiple of both 4 and 8. The smallest such square would have a side length equal to the LCM(4, 8) = 8 units.
Frequently Asked Questions (FAQ)
Q1: What is the difference between LCM and GCD?
A1: The Least Common Multiple (LCM) is the smallest positive integer that is divisible by both numbers. The Greatest Common Divisor (GCD) is the largest positive integer that divides both numbers without leaving a remainder. They are inversely related; a higher LCM generally implies a lower GCD, and vice-versa.
Q2: How do I find the LCM of more than two numbers?
A2: You can extend the methods discussed above to find the LCM of more than two numbers. For the prime factorization method, you would consider the highest power of each prime factor present in the factorization of all the numbers. For the listing multiples method, you'd need to list multiples for all numbers until you find the smallest common multiple. For the GCD method, you can apply the method iteratively, finding the LCM of the first two numbers, then finding the LCM of the result and the third number, and so on.
Q3: Is the LCM always greater than or equal to the larger of the two numbers?
A3: Yes. The LCM is always greater than or equal to the largest of the numbers involved. This is because the LCM must be divisible by the larger number.
Q4: Can the LCM of two numbers be equal to one of the numbers?
A4: Yes, this happens when one number is a multiple of the other. In our example, LCM(4, 8) = 8. 8 is a multiple of 4.
Q5: What if one of the numbers is 0?
A5: The LCM of any number and 0 is undefined. Zero has infinitely many multiples, making it impossible to define the least common multiple.
Conclusion
Understanding the LCM of 4 and 8, and the broader concept of LCM, is crucial for developing a strong foundation in mathematics. From simple arithmetic tasks to advanced mathematical concepts and real-world applications, the ability to calculate and interpret the LCM proves invaluable. Mastering various methods for calculating the LCM not only helps solve specific problems but also enhances a deeper understanding of number theory and its practical implications across multiple disciplines. The journey of understanding LCM goes beyond simply finding the answer; it's about appreciating the interconnectedness of mathematical concepts and their ability to solve problems in diverse contexts. Remember to practice different methods and explore their applications to solidify your understanding.
Latest Posts
Latest Posts
-
What Does Soler Behaviour Mean
Sep 25, 2025
-
Shape With 9 Sides Name
Sep 25, 2025
-
How Do We Measure Energy
Sep 25, 2025
-
Kinetic Energy From Potential Energy
Sep 25, 2025
-
1 Divided By 3 5
Sep 25, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 4 And 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.