3 5/6 + 2 4/9
dulhadulhi
Sep 21, 2025 · 5 min read
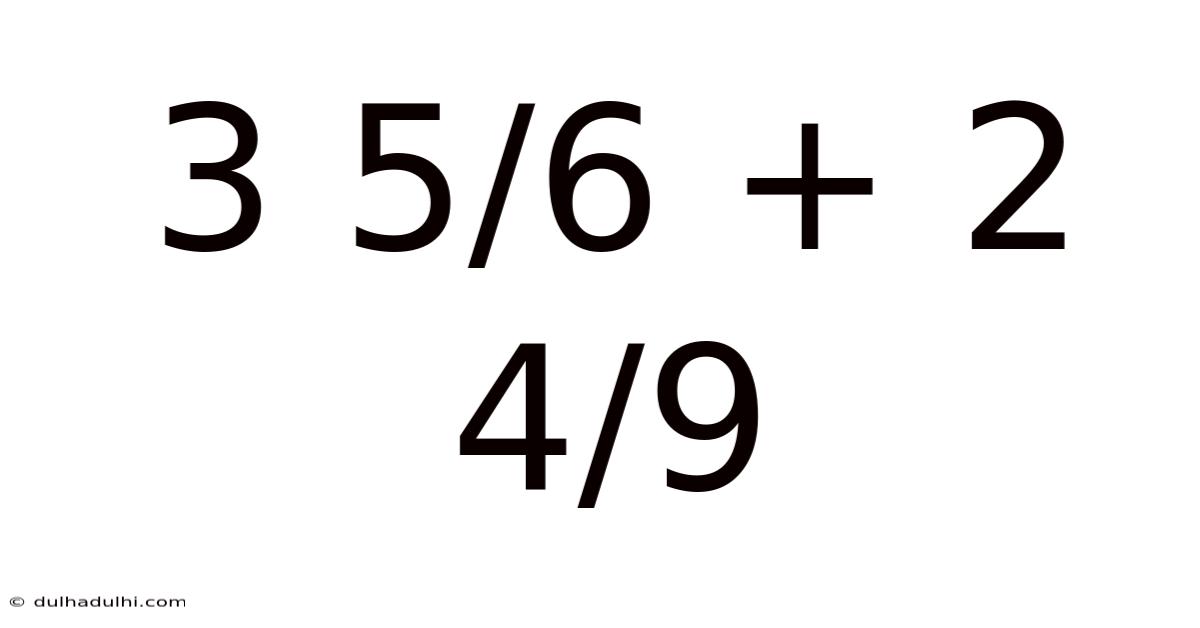
Table of Contents
Mastering Mixed Numbers: A Deep Dive into 3 5/6 + 2 4/9
Adding mixed numbers might seem daunting at first, but with a clear understanding of the process and a bit of practice, it becomes straightforward. This comprehensive guide will walk you through adding 3 5/6 + 2 4/9, explaining each step in detail, providing the scientific rationale behind the method, and addressing frequently asked questions. We'll explore the fundamental concepts of fractions and mixed numbers, ensuring you grasp the underlying principles. This isn't just about getting the right answer; it's about building a solid foundation in arithmetic.
Understanding Mixed Numbers and Fractions
Before tackling the addition problem, let's review the basics. A mixed number combines a whole number and a fraction, like 3 5/6. The whole number represents the number of complete units, while the fraction represents a portion of a unit. A fraction, in its simplest form, is a part of a whole, represented as a numerator (top number) over a denominator (bottom number). The denominator shows how many equal parts the whole is divided into, and the numerator shows how many of those parts we have.
In our problem, 3 5/6 + 2 4/9, we have two mixed numbers. To add them, we need to follow a systematic approach, ensuring we handle both the whole numbers and the fractions correctly.
Step-by-Step Solution: Adding 3 5/6 + 2 4/9
-
Find a Common Denominator: Before we can add the fractions, we need a common denominator. The denominators in our problem are 6 and 9. To find the least common denominator (LCD), we find the least common multiple (LCM) of 6 and 9.
- Multiples of 6: 6, 12, 18, 24...
- Multiples of 9: 9, 18, 27...
The least common multiple of 6 and 9 is 18. Therefore, 18 is our common denominator.
-
Convert Fractions to Equivalent Fractions: Now we convert 5/6 and 4/9 into equivalent fractions with a denominator of 18.
- For 5/6: We multiply both the numerator and the denominator by 3 (because 6 x 3 = 18): (5 x 3) / (6 x 3) = 15/18
- For 4/9: We multiply both the numerator and the denominator by 2 (because 9 x 2 = 18): (4 x 2) / (9 x 2) = 8/18
-
Rewrite the Problem with Equivalent Fractions: Our problem now becomes: 3 15/18 + 2 8/18
-
Add the Whole Numbers: Add the whole numbers together: 3 + 2 = 5
-
Add the Fractions: Now, add the fractions together: 15/18 + 8/18 = 23/18
-
Simplify the Improper Fraction: The result, 23/18, is an improper fraction because the numerator (23) is larger than the denominator (18). We convert this into a mixed number:
23 ÷ 18 = 1 with a remainder of 5. So, 23/18 is equal to 1 5/18.
-
Combine the Whole Number and Fraction: Finally, combine the whole number from step 4 and the mixed number from step 6: 5 + 1 5/18 = 6 5/18
Therefore, 3 5/6 + 2 4/9 = 6 5/18
The Mathematical Rationale: Why This Method Works
The method we used is based on fundamental principles of fraction arithmetic and the properties of real numbers.
-
Equivalence of Fractions: Converting fractions to equivalent fractions with a common denominator is crucial because it allows us to directly add the numerators. Multiplying the numerator and denominator of a fraction by the same non-zero number does not change the value of the fraction; it simply represents the same portion of a whole using different-sized pieces.
-
Distributive Property: The process of adding mixed numbers implicitly uses the distributive property of multiplication over addition. When we separate the whole numbers and fractions, we're essentially applying the distributive property in reverse.
-
Addition of Fractions: Adding fractions with a common denominator is straightforward. We simply add the numerators and keep the denominator the same. This is because we're adding the same-sized parts of a whole.
-
Improper Fractions and Mixed Numbers: Converting an improper fraction to a mixed number involves division. This represents regrouping the parts to form complete units.
Frequently Asked Questions (FAQ)
-
Q: Can I add the whole numbers and fractions separately in any order?
A: Yes, the commutative property of addition allows you to add the numbers in any order. You'll still arrive at the same answer.
-
Q: What if the fractions don't have a simple common denominator?
A: You can always find a common denominator by multiplying the denominators together. Although, it's more efficient to use the least common multiple (LCM) to minimize the numbers you work with and simplify the calculation.
-
Q: What if I get a different answer?
A: Double-check each step: did you find the correct common denominator? Did you correctly convert the fractions? Did you correctly add the whole numbers and fractions? Carefully review your calculations to identify any errors.
-
Q: Are there other methods to add mixed numbers?
A: Yes, some people prefer converting mixed numbers to improper fractions first before adding. This can simplify the calculation for some but can also lead to larger numbers to deal with. Both methods are valid and will provide the same correct answer.
-
Q: How can I practice more problems like this?
A: Practice is key! Work through a variety of examples, starting with simpler problems and gradually increasing the complexity. You can find many worksheets and online resources to help you practice.
Conclusion: Building Confidence in Fraction Arithmetic
Adding mixed numbers, such as 3 5/6 + 2 4/9, might seem challenging initially, but by breaking down the problem into smaller, manageable steps and understanding the underlying mathematical principles, you can master this essential arithmetic skill. Remember the importance of finding a common denominator, converting fractions to equivalent fractions, and simplifying improper fractions to mixed numbers. With consistent practice, you’ll build confidence and fluency in handling mixed number addition and other fraction operations. This skill forms a crucial building block for more advanced mathematical concepts, so mastering it now will pay dividends in your future studies. Embrace the process, practice diligently, and you will see your mathematical abilities flourish.
Latest Posts
Latest Posts
-
What Is Length Width Height
Sep 21, 2025
-
How Many Ml In Mug
Sep 21, 2025
-
Hcf Of 15 And 18
Sep 21, 2025
-
How Big Is 6 5 Inches
Sep 21, 2025
-
Charles Darwin On Galapagos Islands
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 3 5/6 + 2 4/9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.