Hcf Of 15 And 18
dulhadulhi
Sep 21, 2025 · 7 min read
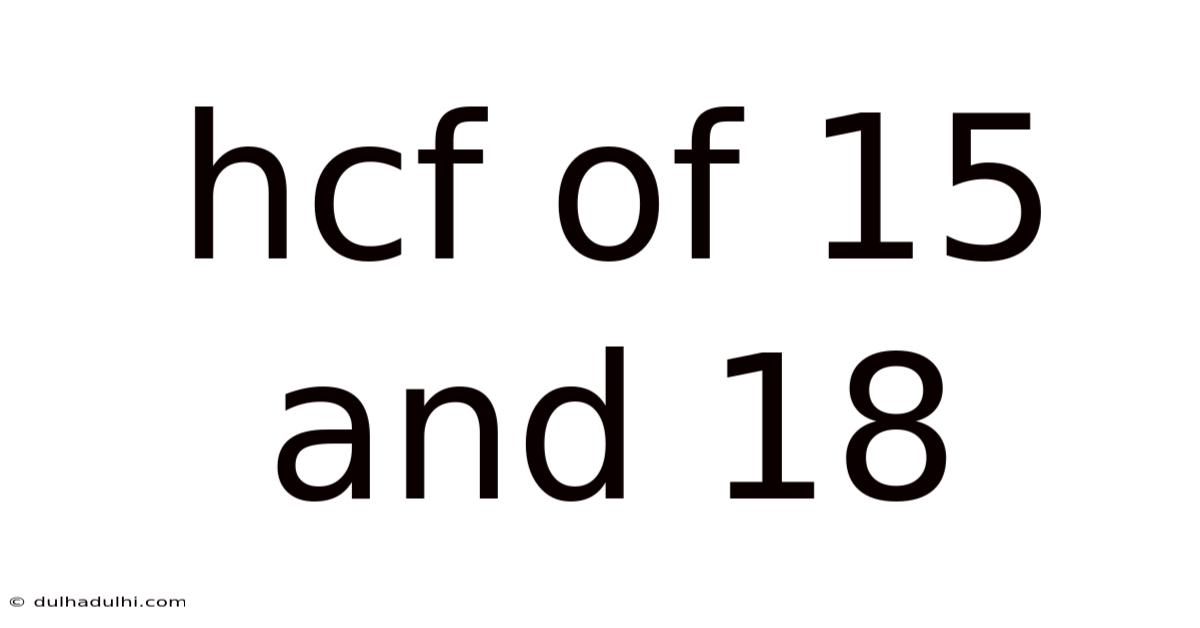
Table of Contents
Finding the Highest Common Factor (HCF) of 15 and 18: A Comprehensive Guide
Finding the Highest Common Factor (HCF), also known as the Greatest Common Divisor (GCD), of two numbers is a fundamental concept in mathematics. This article will delve deep into the process of calculating the HCF of 15 and 18, exploring various methods and providing a thorough understanding of the underlying principles. We'll cover prime factorization, the Euclidean algorithm, and even explore the broader applications of finding HCFs in various mathematical contexts. Understanding HCFs is crucial for simplifying fractions, solving algebraic equations, and laying a solid foundation for more advanced mathematical concepts.
Introduction to Highest Common Factor (HCF)
The Highest Common Factor (HCF) of two or more numbers is the largest number that divides each of them without leaving a remainder. In simpler terms, it's the biggest number that is a factor of both numbers. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12. The factors of 18 are 1, 2, 3, 6, 9, and 18. The common factors of 12 and 18 are 1, 2, 3, and 6. The highest of these common factors is 6, therefore, the HCF of 12 and 18 is 6. This article will focus specifically on finding the HCF of 15 and 18.
Method 1: Prime Factorization
Prime factorization is a powerful technique for determining the HCF of any two numbers. It involves breaking down each number into its prime factors – numbers that are only divisible by 1 and themselves. Let's apply this method to find the HCF of 15 and 18:
1. Prime Factorization of 15:
15 can be broken down as follows:
15 = 3 x 5
Both 3 and 5 are prime numbers.
2. Prime Factorization of 18:
18 can be broken down as follows:
18 = 2 x 3 x 3 = 2 x 3²
Both 2 and 3 are prime numbers.
3. Identifying Common Prime Factors:
Now, let's compare the prime factorizations of 15 and 18:
15 = 3 x 5 18 = 2 x 3²
The only common prime factor between 15 and 18 is 3.
4. Calculating the HCF:
The HCF is the product of the common prime factors raised to the lowest power. In this case, the only common prime factor is 3, and its lowest power is 3¹. Therefore, the HCF of 15 and 18 is 3.
Method 2: Listing Factors
Another straightforward method to find the HCF is by listing all the factors of each number and then identifying the largest common factor.
1. Factors of 15:
The factors of 15 are 1, 3, 5, and 15.
2. Factors of 18:
The factors of 18 are 1, 2, 3, 6, 9, and 18.
3. Common Factors:
Comparing the factors of 15 and 18, we find that the common factors are 1 and 3.
4. Highest Common Factor:
The highest of these common factors is 3. Therefore, the HCF of 15 and 18 is 3.
Method 3: Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the HCF of two numbers, especially when dealing with larger numbers. It's based on the principle that the HCF of two numbers does not change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the HCF.
Let's apply the Euclidean algorithm to 15 and 18:
-
Step 1: Since 18 > 15, we subtract 15 from 18: 18 - 15 = 3. Now we have the pair (15, 3).
-
Step 2: Now we repeat the process with (15, 3). Since 15 > 3, we subtract 3 from 15 repeatedly until we get a number less than 3: 15 - 3 = 12; 12 - 3 = 9; 9 - 3 = 6; 6 -3 = 3. This gives us the pair (3, 3).
-
Step 3: Since both numbers are now equal to 3, the HCF of 15 and 18 is 3.
Visual Representation using Venn Diagrams
Venn diagrams can offer a visual representation of the HCF concept. While not a direct calculation method, it helps to visualize the common factors. We can represent the factors of 15 and 18 in separate circles, and the overlapping section represents the common factors.
- Circle 1 (15): 1, 3, 5, 15
- Circle 2 (18): 1, 2, 3, 6, 9, 18
The overlapping section would contain 1 and 3. The largest number in the overlapping section is 3, thus confirming the HCF is 3.
Applications of HCF in Real-World Scenarios
The concept of HCF extends beyond abstract mathematical exercises; it has practical applications in various real-world situations:
-
Simplifying Fractions: Finding the HCF is crucial for simplifying fractions to their lowest terms. For instance, the fraction 15/18 can be simplified by dividing both the numerator (15) and the denominator (18) by their HCF (3), resulting in the simplified fraction 5/6.
-
Dividing Objects Equally: If you have 15 apples and 18 oranges, and you want to divide them into identical bags with the maximum number of fruits in each bag, you would need to find the HCF of 15 and 18 (which is 3). You can create 3 identical bags, each containing 5 apples and 6 oranges.
-
Measurement and Geometry: HCF is used in determining the largest possible square tile that can be used to completely cover a rectangular floor of specific dimensions. For example, if a floor measures 15 meters by 18 meters, the largest square tile that can be used would have sides of length equal to the HCF of 15 and 18 (3 meters).
-
Music Theory: In music theory, the HCF is used in determining the greatest common divisor of two musical intervals. This helps in understanding the relationships between different musical notes and chords.
Understanding the Concept of Factors and Divisors
Before moving on, it’s essential to clarify the terms “factors” and “divisors.” These terms are often used interchangeably. A factor or divisor of a number is a whole number that divides the given number without leaving a remainder. For example, the factors of 18 are 1, 2, 3, 6, 9, and 18 because each of these numbers divides 18 evenly.
Frequently Asked Questions (FAQ)
Q1: What is the difference between HCF and LCM?
The Highest Common Factor (HCF) is the largest number that divides both numbers without leaving a remainder, while the Least Common Multiple (LCM) is the smallest number that is a multiple of both numbers. They are related inversely; the product of the HCF and LCM of two numbers equals the product of the two numbers.
Q2: Can the HCF of two numbers be 1?
Yes, if two numbers have no common factors other than 1, their HCF is 1. Such numbers are called relatively prime or coprime.
Q3: Can I use a calculator to find the HCF?
Many calculators have built-in functions to calculate the HCF (or GCD). You can also find numerous online calculators that can perform this function.
Conclusion
Finding the HCF of 15 and 18, as demonstrated using three different methods, highlights the fundamental importance of this concept in mathematics. Understanding the underlying principles of prime factorization, the Euclidean algorithm, and the concept of factors enables us to tackle more complex mathematical problems and appreciate the practical applications of HCF in various fields. The HCF is a cornerstone of number theory and plays a vital role in simplifying calculations and solving problems across various disciplines. Remember that selecting the most appropriate method often depends on the size and complexity of the numbers involved. For smaller numbers, listing factors might be quickest, while for larger numbers, the Euclidean algorithm proves more efficient. Mastering these methods provides a solid foundation for further explorations in mathematics.
Latest Posts
Latest Posts
-
Is Blue Or Brown Live
Sep 21, 2025
-
How Are Hen Eggs Fertilized
Sep 21, 2025
-
Diagram Of Destructive Plate Boundary
Sep 21, 2025
-
Static Pressure Vs Dynamic Pressure
Sep 21, 2025
-
Does Stress Cause Urine Infection
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about Hcf Of 15 And 18 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.