12 15 In Simplest Form
dulhadulhi
Sep 23, 2025 · 6 min read
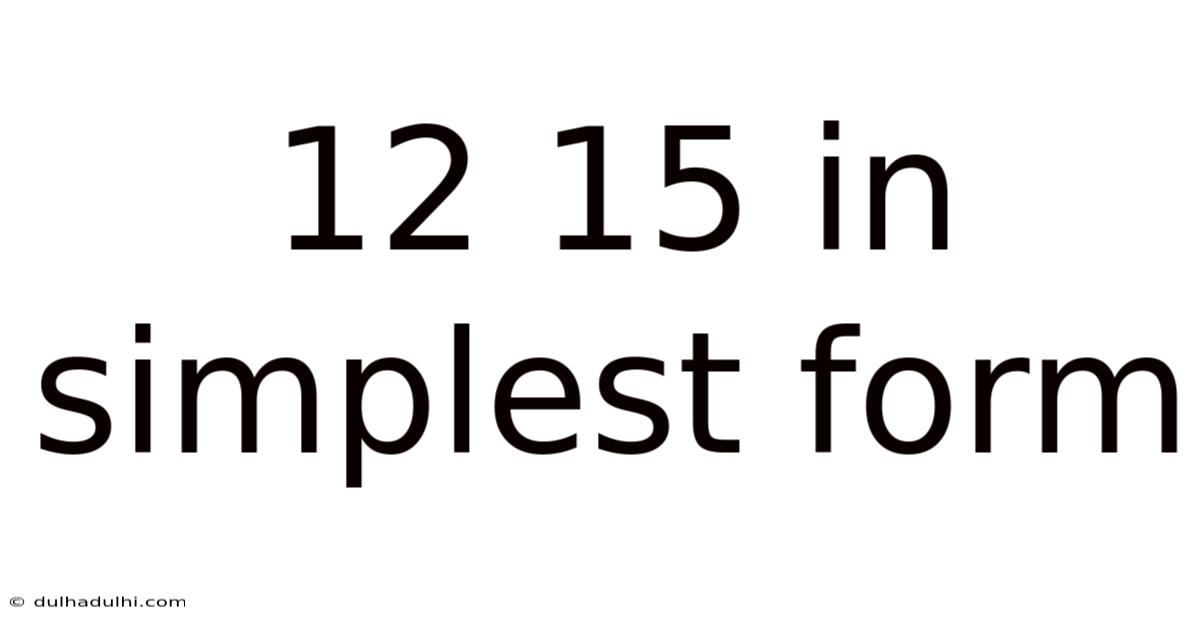
Table of Contents
Simplifying Fractions: A Deep Dive into 12/15
Understanding fractions is a fundamental concept in mathematics, essential for various applications in everyday life and advanced studies. This article will thoroughly explore the simplification of fractions, using the example of 12/15. We'll delve into the process, explain the underlying mathematical principles, and address common questions to provide a comprehensive understanding of this crucial topic. By the end, you'll not only know the simplest form of 12/15 but also possess the skills to simplify any fraction with confidence.
Introduction: What are Fractions and Why Simplify Them?
A fraction represents a part of a whole. It's written as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). For instance, in the fraction 12/15, 12 is the numerator and 15 is the denominator. This means we have 12 parts out of a total of 15 equal parts.
Simplifying fractions, also known as reducing fractions or expressing them in their lowest terms, means finding an equivalent fraction where the numerator and denominator are smaller but still represent the same proportion. Why is this important?
-
Clarity: Simplified fractions are easier to understand and compare. Imagine comparing 12/15 and 24/30 – they are the same, but 12/15 is much clearer.
-
Efficiency: In calculations, simplified fractions make computations simpler and less prone to errors.
-
Standard Form: In mathematics and many applications, representing fractions in their simplest form is a standard practice, ensuring consistency and easy communication.
Finding the Greatest Common Divisor (GCD)
The key to simplifying a fraction lies in finding the greatest common divisor (GCD) of the numerator and the denominator. The GCD is the largest number that divides both the numerator and the denominator without leaving a remainder. Let's find the GCD of 12 and 15.
Several methods exist to determine the GCD:
-
Listing Factors: List all the factors (numbers that divide evenly) of 12 and 15:
Factors of 12: 1, 2, 3, 4, 6, 12 Factors of 15: 1, 3, 5, 15
The common factors are 1 and 3. The greatest of these is 3. Therefore, the GCD of 12 and 15 is 3.
-
Prime Factorization: This method involves breaking down each number into its prime factors (numbers divisible only by 1 and themselves).
12 = 2 x 2 x 3 15 = 3 x 5
The common prime factor is 3. Therefore, the GCD is 3.
-
Euclidean Algorithm: This is a more efficient method for larger numbers. It involves repeatedly applying division with remainder until the remainder is 0. The last non-zero remainder is the GCD.
15 ÷ 12 = 1 remainder 3 12 ÷ 3 = 4 remainder 0
The last non-zero remainder is 3, so the GCD is 3.
Simplifying 12/15: The Steps
Now that we know the GCD of 12 and 15 is 3, we can simplify the fraction:
-
Divide the numerator by the GCD: 12 ÷ 3 = 4
-
Divide the denominator by the GCD: 15 ÷ 3 = 5
Therefore, the simplified form of 12/15 is 4/5. This means that 12/15 and 4/5 represent the same proportion; they are equivalent fractions.
Visual Representation: Understanding Equivalence
Imagine a pizza cut into 15 equal slices. 12/15 represents having 12 of those slices. If we group these slices into sets of 3, we have 4 groups of 3 slices each. Now imagine the pizza cut into only 5 slices (by grouping the previous 15 slices into sets of 3). Having 4 of these larger slices is exactly the same as having 12 of the original 15 slices. This visually demonstrates the equivalence of 12/15 and 4/5.
Mathematical Explanation: The Property of Equivalent Fractions
The process of simplifying fractions relies on the fundamental property of fractions: multiplying or dividing both the numerator and the denominator by the same non-zero number results in an equivalent fraction.
In our case:
(12 ÷ 3) / (15 ÷ 3) = 4/5
We divided both the numerator and denominator by their GCD (3), resulting in the simplified fraction 4/5. This process doesn't change the value of the fraction, only its representation.
Simplifying Fractions with Larger Numbers
The same principles apply when simplifying fractions with larger numbers. The key is always to find the GCD. Let's consider an example:
Simplify 72/96:
-
Find the GCD: Using the Euclidean algorithm or prime factorization, the GCD of 72 and 96 is 24.
-
Divide: 72 ÷ 24 = 3 and 96 ÷ 24 = 4
-
Simplified Fraction: 72/96 simplifies to 3/4.
Dealing with Improper Fractions
An improper fraction is one where the numerator is greater than or equal to the denominator (e.g., 12/5). Simplifying improper fractions follows the same procedure:
Simplify 18/6:
-
Find the GCD: The GCD of 18 and 6 is 6.
-
Divide: 18 ÷ 6 = 3 and 6 ÷ 6 = 1
-
Simplified Fraction: 18/6 simplifies to 3/1, which is equivalent to the whole number 3.
Frequently Asked Questions (FAQ)
Q: What if the GCD is 1?
A: If the GCD of the numerator and denominator is 1, the fraction is already in its simplest form. For example, 7/11 is already simplified because the GCD of 7 and 11 is 1.
Q: Can I simplify a fraction by dividing the numerator and denominator by different numbers?
A: No, this will change the value of the fraction and result in an incorrect simplification. You must always divide both the numerator and the denominator by the same number (specifically, the GCD).
Q: Are there any shortcuts for simplifying fractions?
A: For some simple fractions, you might be able to quickly identify common factors and simplify mentally. However, for larger numbers, using the methods described above (listing factors, prime factorization, or the Euclidean algorithm) is more reliable.
Q: Why is simplifying fractions important in real-world applications?
A: Simplifying fractions is crucial in many fields, such as cooking (measuring ingredients), construction (calculating measurements), and engineering (designing structures). It improves accuracy and efficiency in calculations and makes understanding proportions easier.
Conclusion: Mastering Fraction Simplification
Simplifying fractions is a fundamental mathematical skill with broad applications. By understanding the concept of the greatest common divisor and applying the steps outlined in this article, you can confidently simplify any fraction, making your mathematical work clearer, more efficient, and accurate. Remember, the goal is always to find the equivalent fraction with the smallest possible numerator and denominator, ensuring a clear and concise representation of the proportion. Practice makes perfect, so keep working with different examples, and you'll soon master this essential skill.
Latest Posts
Latest Posts
-
What Are Factors For 33
Sep 23, 2025
-
Biggest Gland In Human Body
Sep 23, 2025
-
Lcm For 7 And 9
Sep 23, 2025
-
Greek Numbers 1 To 10
Sep 23, 2025
-
Can Ionic Compounds Conduct Electricity
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 12 15 In Simplest Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.