1/2 A B Sin C
dulhadulhi
Sep 21, 2025 · 6 min read
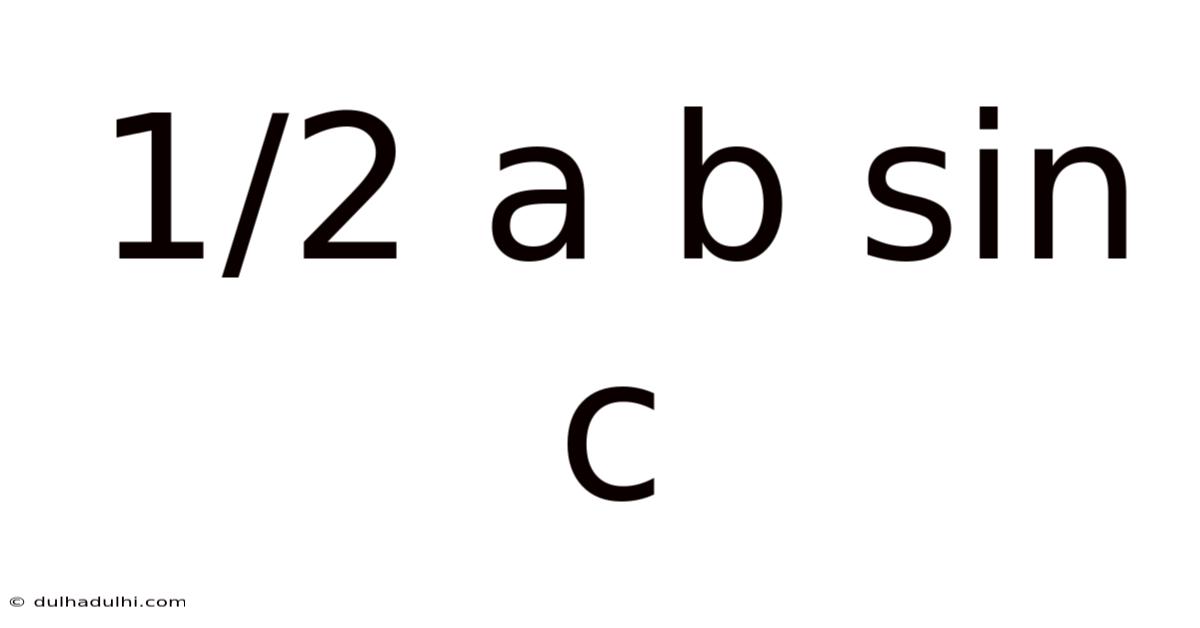
Table of Contents
Decoding the ½ab sin C Formula: Understanding the Area of a Triangle
The formula ½ab sin C is a cornerstone of trigonometry, providing a powerful and elegant method for calculating the area of any triangle. This seemingly simple equation unlocks a deeper understanding of the relationship between a triangle's sides and angles, extending far beyond basic geometry. This article will delve into the formula, exploring its derivation, applications, and significance in various mathematical contexts. We'll unpack the formula step-by-step, clarifying any confusion and highlighting its practical use.
Introduction: Why is ½ab sin C Important?
Understanding how to calculate the area of a triangle is crucial in numerous fields, from surveying and construction to computer graphics and physics. While the familiar base times height divided by two (½bh) formula works well for right-angled triangles and those where the height is easily determined, it proves less practical for more complex shapes. This is where the ½ab sin C formula shines. It offers a universally applicable method, requiring only the knowledge of two sides (a and b) and the included angle (C) between them. This makes it a highly versatile tool for solving a wide range of problems. The formula's elegance lies in its ability to connect seemingly disparate concepts: the lengths of sides and the measure of an angle, both crucial in defining a triangle's shape and size.
Derivation of the ½ab sin C Formula
The derivation of the formula hinges on the understanding of trigonometric ratios within a right-angled triangle. Let's break it down:
-
Constructing the Height: Consider any triangle ABC, with sides a, b, and c opposite to angles A, B, and C respectively. To use the traditional area formula (½bh), we need to find the height (h) of the triangle. We can do this by drawing a perpendicular line from vertex B to side AC (let's call the point where it intersects AC point D). This creates two right-angled triangles: ABD and CBD.
-
Applying Trigonometry: In right-angled triangle ABD, we can use the sine function: sin A = h/c. This means h = c sin A. Similarly, in right-angled triangle CBD, sin C = h/a, leading to h = a sin C. Note: the height 'h' remains the same in both right-angled triangles.
-
Substituting into the Area Formula: The area of triangle ABC is given by ½ * base * height. Using AC (side b) as the base, and the height (h) we derived, we get Area = ½ * b * h. Substituting h = a sin C (from step 2), we get: Area = ½ab sin C. Similarly, using side 'a' as the base and 'h' from h = b sin A we get: Area = ½ab sin A.
This derivation demonstrates that the formula ½ab sin C is a direct consequence of the basic trigonometric ratios and the standard area formula for triangles. This connection highlights the interconnectedness of various mathematical concepts.
Applications and Examples of ½ab sin C
The ½ab sin C formula finds wide application in various scenarios:
-
Surveying and Land Measurement: Surveyors use this formula to calculate the area of irregular plots of land. By measuring two sides and the included angle, they can accurately determine the area without needing to measure the height directly, which can be challenging in uneven terrain.
-
Navigation and Aviation: Determining distances and areas is crucial for navigation. This formula helps calculate the area covered by a flight path or the area of a geographical region using available data points.
-
Engineering and Construction: The formula is used to calculate the area of irregular surfaces, facilitating accurate material estimations for construction projects. This ensures that sufficient materials are available and reduces wastage.
-
Computer Graphics: In computer graphics and game development, the formula is used to render realistic 3D shapes. Accurate area calculations are crucial for rendering lighting effects, shading, and texturing, ensuring the visual representation is accurate and realistic.
-
Physics and Mechanics: Calculating areas is essential for finding centers of mass, moments of inertia, and other crucial parameters used in physical calculations. The formula simplifies the area calculation of triangular structures involved in complex force calculations.
Let's illustrate with an example:
Suppose we have a triangle with sides a = 10 cm and b = 15 cm, and the angle between them (C) is 60 degrees. To find the area, we plug the values into the formula:
Area = ½ * 10 cm * 15 cm * sin 60°
Since sin 60° = √3/2, the area becomes:
Area = ½ * 10 cm * 15 cm * (√3/2) = 65 cm² (approximately).
Exploring the Formula in Different Contexts
The ½ab sin C formula isn't just a standalone calculation; it connects to several other important concepts:
-
Heron's Formula: This formula calculates the area of a triangle using the lengths of its three sides. While seemingly different, Heron's formula can be derived using the ½ab sin C formula and the cosine rule, showcasing the intricate connections within trigonometry.
-
Vectors: The area of a triangle can also be calculated using vector cross products. The magnitude of the cross product of two vectors representing two sides of the triangle is directly related to the ½ab sin C formula, reinforcing the link between geometry and vector algebra.
-
Coordinate Geometry: If the coordinates of the vertices of a triangle are known, we can calculate the lengths of the sides and the included angles using distance formula and trigonometric functions, subsequently utilizing the ½ab sin C formula to determine the area.
Frequently Asked Questions (FAQ)
-
Q: Can I use this formula for any type of triangle?
- A: Yes, the ½ab sin C formula works for all types of triangles – acute, obtuse, or right-angled. This universality is a key advantage over other area formulas that might have limitations.
-
Q: What if I only know the lengths of all three sides?
- A: If you only know the side lengths (a, b, c), you would use Heron's formula to calculate the area.
-
Q: What happens if the angle C is 90 degrees?
- A: If C = 90 degrees, sin C = 1, and the formula simplifies to ½ab, which is equivalent to the familiar ½ base * height formula for a right-angled triangle where a and b are the legs.
-
Q: What are the units of the area calculated using this formula?
- A: The units of the area will be the square of the units used for the side lengths (e.g., cm², m², etc.).
-
Q: Can I use radians instead of degrees for the angle C?
- A: Yes, you can use radians for the angle C, but make sure your calculator is set to the appropriate mode (radians or degrees).
Conclusion: The Enduring Power of ½ab sin C
The ½ab sin C formula is more than just a tool for calculating the area of a triangle; it's a testament to the elegance and interconnectedness of mathematical concepts. Its derivation highlights the power of trigonometry, and its applications span various fields, emphasizing its practical significance. Understanding this formula not only improves problem-solving skills but also deepens one's appreciation for the fundamental principles governing geometry and trigonometry. By mastering this formula, you gain a powerful tool that unlocks a wider understanding of the world around us, from the measurement of land to the intricacies of computer-generated imagery. Its simple yet profound nature makes it a vital component of any mathematical toolkit. This formula serves as a stepping stone to more advanced concepts in mathematics and science, underscoring its enduring importance in various disciplines.
Latest Posts
Latest Posts
-
68 Degrees Fahrenheit In Celsius
Sep 21, 2025
-
Steel Is A Magnetic Material
Sep 21, 2025
-
Weather In Europe In December
Sep 21, 2025
-
Branch Of Mathematics 8 Letters
Sep 21, 2025
-
3 5 Divided By 2
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 1/2 A B Sin C . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.