3 5 Divided By 2
dulhadulhi
Sep 21, 2025 · 6 min read
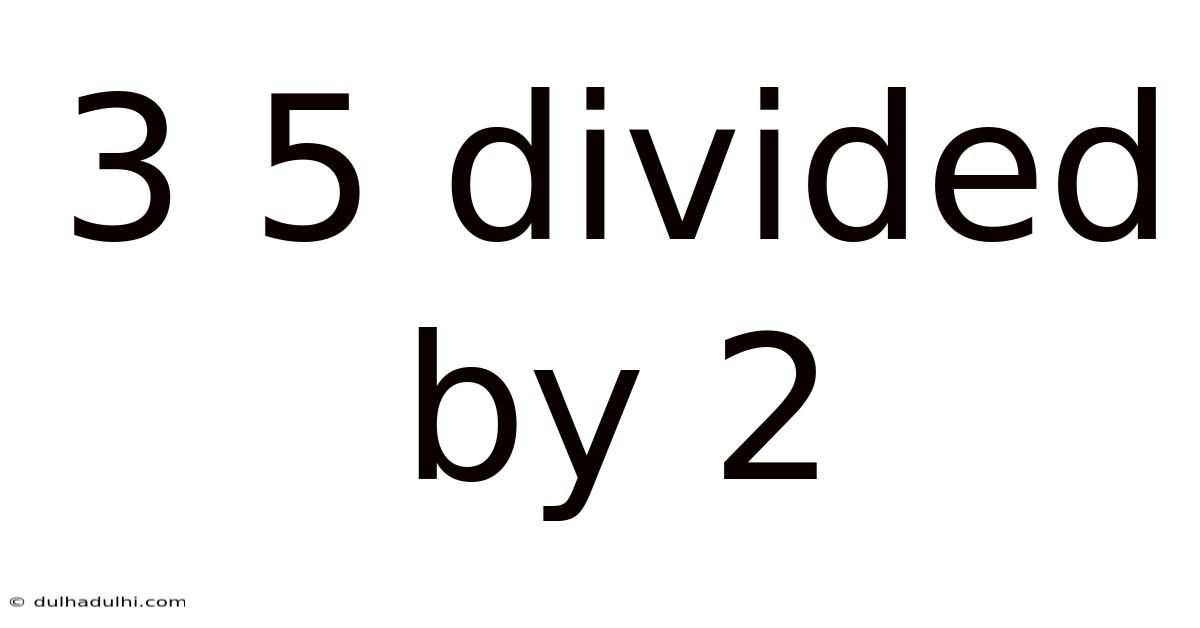
Table of Contents
Decoding 3.5 Divided by 2: A Deep Dive into Division and Decimal Operations
Understanding division, especially when dealing with decimals, is a fundamental skill in mathematics. This article will thoroughly explore the seemingly simple calculation of 3.5 divided by 2, delving into the process, the underlying mathematical principles, and exploring various applications and extensions of this concept. We'll cover everything from the basic steps to advanced interpretations, ensuring a comprehensive understanding for readers of all levels. This exploration will also cover related concepts like fractions and their decimal equivalents, providing a robust foundation in arithmetic operations.
Understanding the Fundamentals of Division
Before diving into the specific calculation of 3.5 ÷ 2, let's refresh our understanding of division. Division is essentially the inverse operation of multiplication. It determines how many times one number (the divisor) is contained within another number (the dividend). The result of the division is called the quotient. In the case of 3.5 ÷ 2, 3.5 is the dividend and 2 is the divisor. We are seeking the quotient representing how many times 2 fits into 3.5.
We can visualize this using everyday examples. Imagine you have 3.5 pizzas and want to share them equally between two people. How much pizza does each person get? This is precisely the question answered by 3.5 ÷ 2.
Step-by-Step Calculation: 3.5 ÷ 2
There are several ways to approach this division problem. Let's explore the most common methods:
Method 1: Long Division
Long division is a systematic method for dividing larger numbers, and it works equally well with decimals. Here's how to solve 3.5 ÷ 2 using long division:
-
Set up the problem: Write 3.5 inside the long division symbol (⟌) and 2 outside.
-
Divide the whole number part: 2 goes into 3 once (2 x 1 = 2). Write '1' above the 3.
-
Subtract: Subtract 2 from 3, leaving 1.
-
Bring down the decimal: Bring down the 5 from the decimal part, resulting in 15.
-
Divide the decimal part: 2 goes into 15 seven times (2 x 7 = 14). Write '7' above the 5.
-
Subtract again: Subtract 14 from 15, leaving 1.
-
Add a zero and continue: Since we have a remainder, we add a zero after the decimal point in the dividend (3.5 becomes 3.50). Bring this zero down, making it 10.
-
Divide again: 2 goes into 10 five times (2 x 5 = 10). Write '5' above the added zero.
-
Final subtraction: Subtract 10 from 10, leaving 0. We have no remainder.
Therefore, 3.5 ÷ 2 = 1.75.
Method 2: Converting to Fractions
Another effective approach involves converting the decimal to a fraction:
-
Represent as a fraction: 3.5 can be written as the improper fraction 7/2 (since 3.5 = 3 + 1/2 = 6/2 + 1/2 = 7/2).
-
Perform fraction division: Dividing by 2 is the same as multiplying by its reciprocal, which is 1/2. So, (7/2) ÷ 2 = (7/2) x (1/2) = 7/4.
-
Convert back to decimal: To convert 7/4 to a decimal, we perform the division: 7 ÷ 4 = 1.75.
Again, we arrive at the answer: 1.75.
Mathematical Principles at Play
The seemingly simple calculation of 3.5 ÷ 2 touches upon several important mathematical principles:
-
Decimal Representation: The use of decimals highlights the extension of the number system beyond whole numbers, allowing for the representation of fractional parts.
-
Distributive Property: Implicitly, we are using the distributive property when we divide the whole number part and the decimal part separately in long division.
-
Reciprocal Relationships: The fraction method clearly illustrates the reciprocal relationship between multiplication and division.
-
Place Value: The long division method reinforces understanding of place value in decimals, as we carry over and add zeros as needed.
Real-World Applications
The ability to perform this type of division is crucial in various real-world situations:
-
Sharing Resources: As mentioned earlier, sharing items equally (pizzas, money, etc.) often involves dividing decimals.
-
Measurement Conversions: Converting units of measurement (e.g., meters to centimeters) often necessitates decimal division.
-
Financial Calculations: Many financial calculations, such as calculating unit prices or splitting bills, involve dividing decimals.
-
Scientific Computations: In science and engineering, precise measurements and calculations frequently involve decimal division.
-
Baking and Cooking: Following recipes often requires dividing quantities, sometimes resulting in decimal values.
Expanding the Concept: Dividing Larger Decimals and Dealing with Remainders
The principles demonstrated in calculating 3.5 ÷ 2 can be extended to more complex scenarios:
-
Dividing larger decimals: The long division method seamlessly adapts to larger decimal numbers. The process remains consistent, ensuring an accurate quotient.
-
Dealing with remainders: If the division does not result in a whole number, a remainder will exist. This remainder can be expressed as a fraction or carried out further by adding more zeros after the decimal point, as shown in the long division example above. This process can be continued until a desired level of accuracy is achieved or the remainder becomes zero.
-
Dividing by decimals: When dividing by a decimal, the first step is typically to convert the divisor into a whole number by multiplying both the dividend and divisor by a power of 10. This simplifies the division process.
Frequently Asked Questions (FAQ)
Q: What if I don't have a calculator?
A: Long division, as detailed above, is a reliable method for calculating 3.5 ÷ 2 without a calculator. Alternatively, you can convert the decimal to a fraction and perform fraction division.
Q: Why is it important to understand decimal division?
A: Understanding decimal division is fundamental for numerous real-world applications, including financial calculations, scientific measurements, and everyday tasks. It enhances mathematical problem-solving skills.
Q: Can I use a calculator to verify the answer?
A: Yes, using a calculator is a great way to check your work and ensure accuracy. Most calculators will provide the answer 1.75 for 3.5 ÷ 2.
Conclusion: Mastering Decimal Division
The seemingly simple problem of 3.5 ÷ 2 provides a valuable opportunity to reinforce fundamental mathematical skills, such as long division, fraction manipulation, and understanding decimal place value. By understanding the process and the underlying mathematical principles, we can effectively solve this type of problem and apply this knowledge to various real-world scenarios, showcasing the practical significance of decimal division in everyday life and beyond. The methods discussed here – long division and fraction conversion – are versatile and can be applied to solve a wide range of division problems involving decimals. Through consistent practice and a solid understanding of these techniques, you will build confidence and proficiency in your mathematical abilities.
Latest Posts
Latest Posts
-
How Long Do Locusts Live
Sep 21, 2025
-
3 To The Power 7
Sep 21, 2025
-
Hcf Of 12 And 15
Sep 21, 2025
-
Does Facilitated Diffusion Require Energy
Sep 21, 2025
-
What Animals Do Giraffes Eat
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 3 5 Divided By 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.