What Is 5 Of 30000
dulhadulhi
Sep 22, 2025 · 4 min read
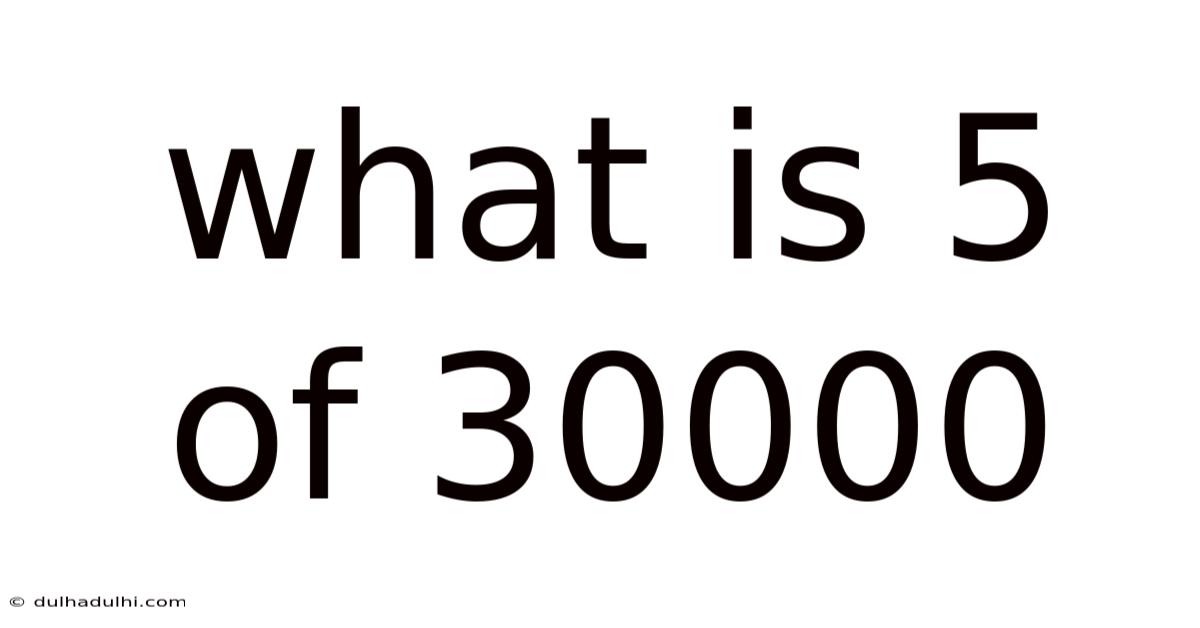
Table of Contents
What is 5/30000? Understanding Fractions and Their Applications
This article explores the seemingly simple question: "What is 5/30000?" While the calculation itself is straightforward, delving into the meaning and applications of this fraction opens a door to a deeper understanding of mathematical concepts and their real-world relevance. We'll break down the calculation, explore different ways to represent the fraction, and discuss its applications in various fields. Understanding fractions like 5/30000 is crucial for anyone working with percentages, ratios, proportions, and statistical analysis.
Understanding the Fraction 5/30000
The fraction 5/30000 represents a part of a whole. The numerator (5) indicates the number of parts we're considering, while the denominator (30000) represents the total number of equal parts that make up the whole. In simpler terms, if we divide a whole into 30,000 equal pieces, the fraction 5/30000 represents 5 of those pieces.
Calculating the Decimal Equivalent
To better understand the magnitude of 5/30000, we can convert it to its decimal equivalent. This is done by dividing the numerator (5) by the denominator (30000):
5 ÷ 30000 = 0.0001666666...
The result is a very small decimal number. The repeating sixes indicate that this decimal is a recurring decimal, meaning the digits repeat infinitely. For practical purposes, we often round this to a specific number of decimal places. Rounding to four decimal places, we get 0.0002.
Simplifying the Fraction
Before proceeding further, it's helpful to simplify the fraction. Both the numerator and denominator are divisible by 5:
5/30000 = 1/6000
This simplified fraction is equivalent to the original fraction and is often easier to work with. It represents one part out of 6000 equal parts.
Representing the Fraction as a Percentage
To express 5/30000 as a percentage, we multiply the decimal equivalent by 100:
0.0001666666... × 100 ≈ 0.0167%
This shows that 5/30000 represents a very small percentage – approximately 0.0167% of the whole.
Real-World Applications: Understanding Small Proportions
While seemingly insignificant, fractions like 5/30000 have practical applications in several fields:
-
Statistics and Probability: Imagine a survey with 30,000 respondents. If 5 respondents gave a particular answer, the fraction 5/30000 represents the proportion of respondents choosing that answer. This is crucial for analyzing survey data and drawing conclusions.
-
Sampling and Quality Control: In manufacturing, if 5 out of 30,000 products are defective, the fraction 5/30000 represents the defect rate. This information is vital for assessing product quality and implementing quality control measures.
-
Scientific Research: Many scientific experiments involve measurements and data analysis. A fraction like 5/30000 could represent a very small change in a measurement or a small proportion of a substance within a larger sample.
Further Exploration: Ratio and Proportion
The fraction 5/30000 can also be viewed as a ratio. It expresses the relationship between 5 and 30000. This ratio can be used to solve proportion problems. For example:
If 5 out of 30000 items are defective, how many defective items would you expect in a batch of 150,000 items?
To solve this, we can set up a proportion:
5/30000 = x/150000
Solving for x, we get:
x = (5 × 150000) / 30000 = 25
This shows that we would expect 25 defective items in a batch of 150,000.
Advanced Concepts: Limits and Infinitesimals
In calculus, the concept of limits explores the behavior of functions as their input approaches a certain value. Understanding small fractions like 5/30000 helps build intuition for these concepts. As the denominator becomes increasingly large (approaching infinity), the fraction approaches zero. This is a fundamental concept in calculus and has significant applications in various fields, including physics and engineering.
Frequently Asked Questions (FAQ)
Q: How do I calculate 5/30000 without a calculator?
A: While a calculator is convenient, you can perform the calculation manually by long division. Alternatively, simplify the fraction first (to 1/6000) and then perform the division. This simplifies the calculation significantly.
Q: What are some other ways to represent 5/30000?
A: Besides decimal and percentage forms, you can represent it as a ratio (5:30000 or 1:6000), or as a simplified fraction (1/6000).
Q: Is 5/30000 a rational number?
A: Yes, 5/30000 is a rational number because it can be expressed as a fraction of two integers (5 and 30000).
Conclusion: The Significance of Small Fractions
While the fraction 5/30000 may seem insignificant at first glance, understanding its calculation, different representations, and applications highlights the importance of mastering fundamental mathematical concepts. From statistical analysis and quality control to scientific research and advanced calculus, the ability to work with and interpret small fractions is crucial across numerous disciplines. This article has provided a comprehensive overview, empowering you to approach similar fractional calculations with greater confidence and understanding. Remember that even the smallest fraction can hold significant meaning within the context of a larger problem. The seemingly simple act of understanding "What is 5/30000?" can unlock a deeper appreciation for the power and versatility of mathematics in our world.
Latest Posts
Latest Posts
-
What Is 171cm In Feet
Sep 22, 2025
-
Sulfate Ion Lewis Dot Structure
Sep 22, 2025
-
How Big Is 50 Grams
Sep 22, 2025
-
Interior Angle Of A Dodecagon
Sep 22, 2025
-
How Far Is 25 Miles
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about What Is 5 Of 30000 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.