What Is 10 Of 45
dulhadulhi
Sep 21, 2025 · 5 min read
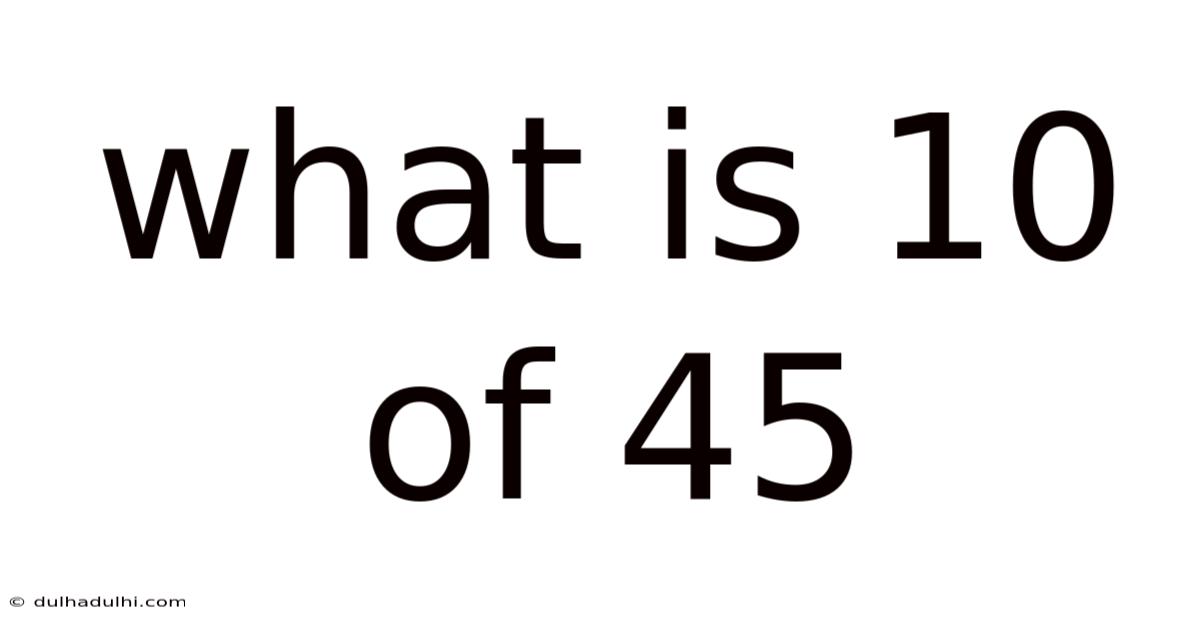
Table of Contents
What is 10% of 45? A Deep Dive into Percentages and Their Applications
Understanding percentages is a fundamental skill in mathematics with widespread applications in everyday life, from calculating discounts and taxes to understanding statistics and financial reports. This article will not only answer the question "What is 10% of 45?" but also delve into the underlying principles of percentage calculations, exploring different methods and providing a solid foundation for tackling similar problems. We will cover various approaches, including mental math techniques, the standard formula, and practical examples to solidify your understanding. By the end, you'll be equipped to confidently calculate percentages in a variety of contexts.
Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The word "percent" literally means "per hundred". So, 10% means 10 out of 100, or 10/100, which simplifies to 1/10. This fractional representation is key to understanding percentage calculations.
Method 1: Using the Standard Percentage Formula
The most common method to calculate a percentage of a number is using the following formula:
Percentage = (Part / Whole) x 100%
Conversely, to find the part (the result of the percentage calculation), we can rearrange the formula:
Part = (Percentage / 100%) x Whole
In our case, we want to find 10% of 45. Therefore:
- Percentage = 10%
- Whole = 45
- Part = Unknown (this is what we need to find)
Substituting these values into the formula:
Part = (10 / 100) x 45
Part = 0.1 x 45
Part = 4.5
Therefore, 10% of 45 is 4.5.
Method 2: Using Fractions
As mentioned earlier, a percentage can be expressed as a fraction. 10% is equivalent to 1/10. Therefore, finding 10% of 45 is the same as finding 1/10 of 45.
Part = (1/10) x 45
Part = 45 / 10
Part = 4.5
This method is particularly useful for simpler percentages like 10%, 25%, 50%, and so on, where the fractional equivalent is easily recognizable.
Method 3: Mental Math Techniques
For certain percentages, particularly 10%, mental math can provide a quick and efficient solution. Since 10% is one-tenth, finding 10% of a number simply involves dividing the number by 10. Dividing 45 by 10 gives us 4.5. This method is excellent for quick calculations without needing a calculator.
Applications of Percentage Calculations
The ability to calculate percentages is crucial in various real-life scenarios:
- Shopping: Calculating discounts on sale items. For instance, a 20% discount on a $100 item would be (20/100) x $100 = $20.
- Taxes: Determining the amount of sales tax or income tax payable. A 6% sales tax on a $50 purchase would be (6/100) x $50 = $3.
- Finance: Calculating interest earned on savings accounts or interest payable on loans.
- Statistics: Interpreting data presented as percentages, such as survey results or market share.
- Science: Representing experimental results and changes in quantities.
Beyond 10%: Calculating Other Percentages of 45
Let's expand our understanding by calculating other percentages of 45:
- 20% of 45: (20/100) x 45 = 9
- 25% of 45: (25/100) x 45 = 11.25 (or (1/4) x 45 = 11.25)
- 50% of 45: (50/100) x 45 = 22.5 (or (1/2) x 45 = 22.5)
- 75% of 45: (75/100) x 45 = 33.75 (or (3/4) x 45 = 33.75)
- 100% of 45: (100/100) x 45 = 45
Working with More Complex Percentages
Calculating percentages doesn't always involve round numbers. Let's consider finding 17.5% of 45:
Part = (17.5 / 100) x 45
Part = 0.175 x 45
Part = 7.875
This demonstrates that the same principles apply to percentages with decimal values.
Frequently Asked Questions (FAQ)
Q1: What is the easiest way to calculate percentages?
A1: The easiest method often depends on the specific percentage. For 10%, 25%, 50%, and 75%, using fractions is often quickest. For other percentages, the standard formula is reliable, and a calculator can assist with more complex calculations. Mental math is useful for simple percentages.
Q2: How can I improve my percentage calculation skills?
A2: Practice is key! Try working through various percentage problems using different methods. Start with simple examples and gradually increase the complexity. Using online quizzes or worksheets can help you reinforce your understanding.
Q3: What if I need to calculate a percentage increase or decrease?
A3: Percentage increase or decrease calculations require a slightly different approach. For an increase, you calculate the increase amount and add it to the original value. For a decrease, you calculate the decrease amount and subtract it from the original value. For example, a 10% increase on 45 is: (10/100) x 45 = 4.5; 45 + 4.5 = 49.5. A 10% decrease on 45 is: (10/100) x 45 = 4.5; 45 - 4.5 = 40.5
Q4: Are there any online tools that can help me calculate percentages?
A4: Yes, many online calculators are available that can quickly and accurately calculate percentages. However, understanding the underlying principles is crucial for applying this knowledge effectively in various situations.
Conclusion
Calculating percentages is a vital skill with numerous practical applications. We've explored various methods for finding the percentage of a number, demonstrating that 10% of 45 is 4.5. By understanding the underlying concepts and practicing different approaches, you can confidently tackle percentage calculations in various contexts, from everyday budgeting to more complex mathematical problems. Remember to choose the method most suitable for the specific problem – whether it's using the standard formula, fractional equivalents, or mental math techniques. Mastering percentages is a valuable asset that will serve you well in various academic and professional endeavors. So, keep practicing and soon you'll find percentage calculations as easy as 1, 2, 3!
Latest Posts
Latest Posts
-
Do Bees Fly At Night
Sep 21, 2025
-
What Is Half Of 24
Sep 21, 2025
-
Does Bees Fly At Night
Sep 21, 2025
-
Ph Level In Distilled Water
Sep 21, 2025
-
Number Of Neutrons In Sodium
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about What Is 10 Of 45 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.