What Is 10 Of 1200
dulhadulhi
Sep 25, 2025 · 5 min read
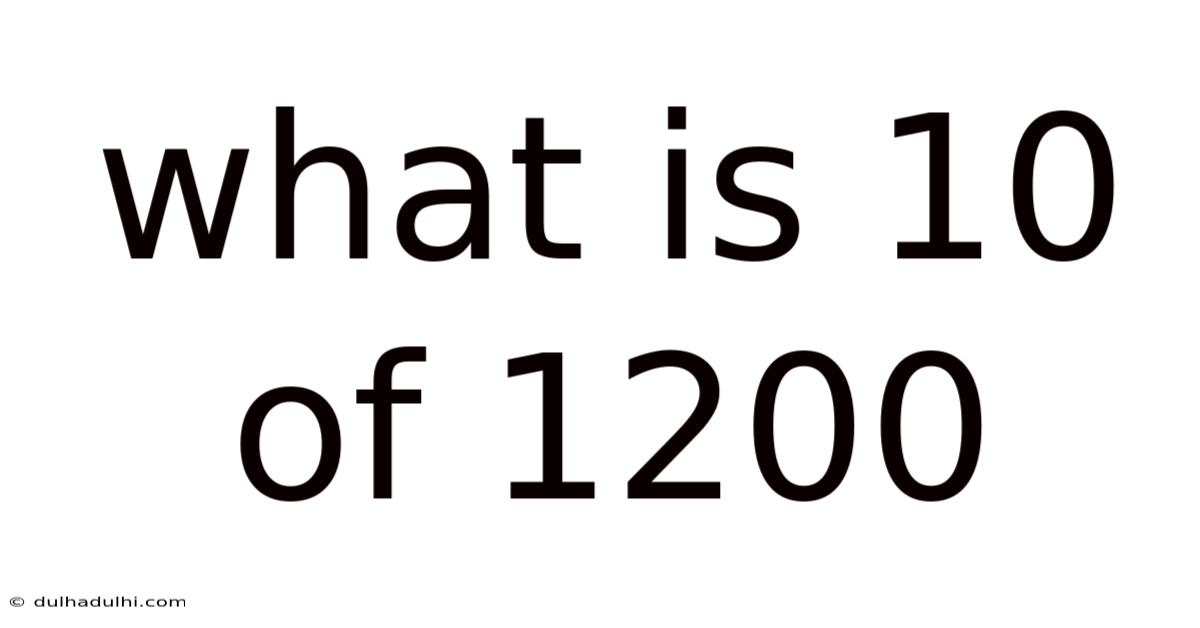
Table of Contents
What is 10% of 1200? A Comprehensive Guide to Percentages and Their Applications
Finding 10% of 1200 might seem like a simple arithmetic problem, but understanding the underlying concepts of percentages is crucial for various aspects of life, from budgeting and finance to understanding statistics and scientific data. This comprehensive guide will not only answer the question "What is 10% of 1200?" but also delve deeper into the world of percentages, explaining their calculation, practical applications, and common misconceptions.
Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The symbol "%" represents "per cent," meaning "out of one hundred." For example, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or the decimal 0.5. Percentages are widely used because they provide a standardized way to compare different quantities or proportions, regardless of their initial sizes.
Calculating Percentages: The Basic Formula
The fundamental formula for calculating a percentage of a number is:
(Percentage/100) * Number = Result
Let's break this down:
- Percentage: This is the percentage you want to find (in our case, 10%).
- 100: This is the denominator, representing the whole (100%).
- Number: This is the number you're taking the percentage of (in our case, 1200).
- Result: This is the answer you're looking for.
Solving the Problem: What is 10% of 1200?
Applying the formula:
(10/100) * 1200 = 120
Therefore, 10% of 1200 is 120.
Alternative Methods for Calculating Percentages
While the above formula is the most fundamental, there are other efficient ways to calculate percentages, especially for simpler calculations like this one:
-
Method 1: Using Decimal Equivalents: 10% can be expressed as the decimal 0.10 (or simply 0.1). Multiplying 1200 by 0.1 gives us the same result: 1200 * 0.1 = 120. This method is often quicker for mental calculations.
-
Method 2: Finding 1% and Scaling Up: To find 10%, first find 1% of 1200. This is done by dividing 1200 by 100: 1200 / 100 = 12. Since 10% is ten times 1%, multiply the result by 10: 12 * 10 = 120. This method is particularly useful when dealing with percentages that aren't simple multiples of 10.
Practical Applications of Percentages
Understanding percentages is essential for navigating various aspects of daily life:
-
Finance and Budgeting: Calculating interest rates, discounts, taxes, tips, and investment returns all involve percentages. For instance, understanding sales tax percentages helps you accurately determine the final cost of a purchase. Similarly, calculating interest on a loan or savings account requires a solid grasp of percentage calculations.
-
Statistics and Data Analysis: Percentages are fundamental in presenting and interpreting statistical data. Graphs and charts often use percentages to illustrate proportions, trends, and comparisons. Understanding percentages allows you to critically analyze data and draw meaningful conclusions.
-
Science and Engineering: Percentages are used in various scientific fields to express concentrations, efficiencies, and errors. For example, the concentration of a solution is often expressed as a percentage.
-
Retail and Sales: Sales discounts, markups, and profit margins are all expressed as percentages. Understanding these percentages allows businesses to manage their pricing strategies effectively and consumers to make informed purchasing decisions.
Common Misconceptions about Percentages
Several common misconceptions surround percentages that can lead to errors in calculations and interpretations:
-
Additive vs. Multiplicative Nature: A common mistake is to assume that percentages are additive. For example, a 10% increase followed by a 10% decrease does not result in the original number. Percentages are multiplicative; they operate on the existing value at each step.
-
Percentage Change vs. Percentage Points: It's crucial to differentiate between percentage change and percentage points. A change from 10% to 20% is a 100% increase (a 10 percentage point increase), not a 10% increase.
-
Misinterpreting Percentage Increases and Decreases: An increase of 10% followed by a decrease of 10% does not return the original value. The final value will be slightly less than the original value due to the multiplicative nature of percentage calculations.
Advanced Applications: Compound Interest and Growth
The concept of percentages extends to more complex scenarios, such as compound interest and exponential growth. Compound interest involves earning interest not only on the principal amount but also on accumulated interest. This results in exponential growth over time. Understanding compound interest is vital for long-term financial planning and investment strategies.
Frequently Asked Questions (FAQ)
-
Q: How do I calculate a percentage increase or decrease?
A: To calculate a percentage increase, subtract the original value from the new value, divide the result by the original value, and multiply by 100. For a percentage decrease, follow the same steps but use the new value minus the original value.
-
Q: How do I convert a fraction to a percentage?
A: Multiply the fraction by 100. For example, 1/4 * 100 = 25%, meaning 1/4 is equal to 25%.
-
Q: How do I convert a decimal to a percentage?
A: Multiply the decimal by 100 and add the "%" symbol. For example, 0.75 * 100 = 75%, meaning 0.75 is equal to 75%.
-
Q: What is the difference between percentage and proportion?
A: While related, percentage and proportion represent slightly different concepts. A proportion expresses a part of a whole as a ratio, while a percentage specifically expresses that ratio as a fraction of 100. A percentage is a specific type of proportion.
Conclusion
Finding 10% of 1200 is a simple calculation, but it serves as a gateway to understanding the broader applications of percentages. Mastering percentage calculations is crucial for success in various aspects of life, from personal finance to professional endeavors. By understanding the basic formula, alternative calculation methods, and common pitfalls, you can confidently tackle percentage-related problems and make informed decisions in various situations. Remember to always double-check your work and ensure you understand the context of the percentage calculation to avoid misinterpretations. With practice and a firm grasp of the concepts, percentages will become an indispensable tool in your mathematical toolkit.
Latest Posts
Latest Posts
-
What Are Mutually Exclusive Events
Sep 25, 2025
-
Am Radio Stations By Frequency
Sep 25, 2025
-
1 82 M In Feet Inches
Sep 25, 2025
-
Biggest Dunes In The World
Sep 25, 2025
-
Formation Of Av Shaped Valley
Sep 25, 2025
Related Post
Thank you for visiting our website which covers about What Is 10 Of 1200 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.