What Is 1/2 Of 1
dulhadulhi
Sep 25, 2025 · 5 min read
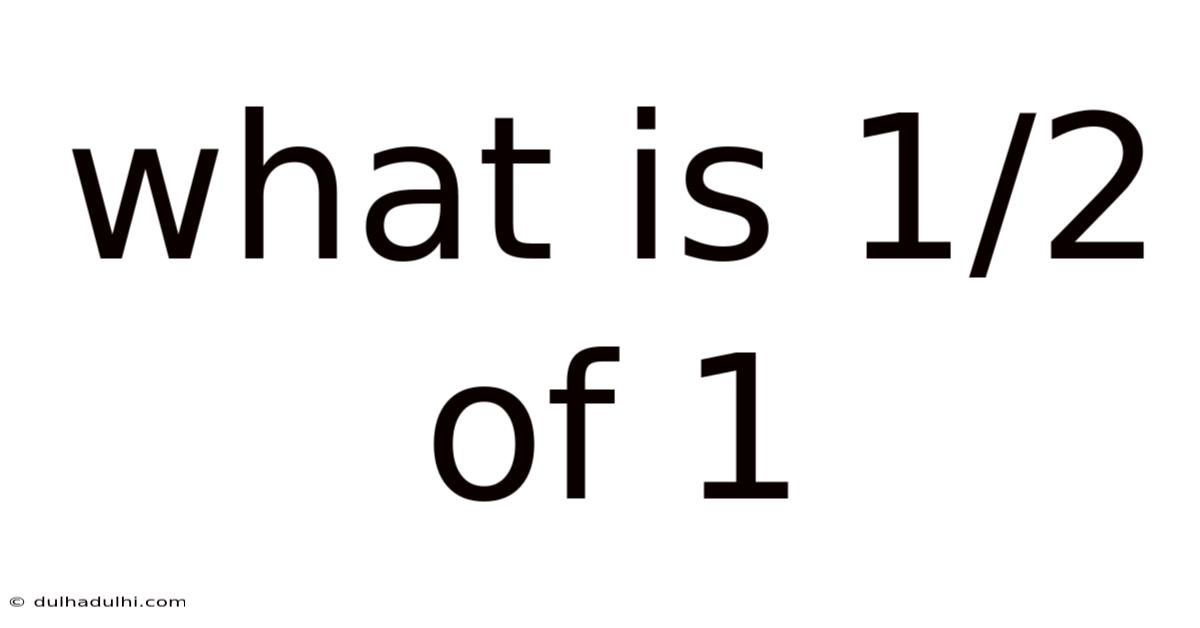
Table of Contents
What is 1/2 of 1? Unpacking Fractions and Their Applications
This seemingly simple question, "What is 1/2 of 1?", opens the door to a deeper understanding of fractions, their representation, and their widespread application in various fields. While the answer might seem immediately obvious to many, exploring the underlying concepts reveals the foundational role fractions play in mathematics and beyond. This article will delve into this seemingly basic calculation, exploring the theoretical underpinnings, practical applications, and addressing common misconceptions surrounding fractions.
Understanding Fractions: A Foundational Concept
A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). The denominator indicates the total number of equal parts the whole is divided into, while the numerator indicates how many of those parts are being considered. In the context of "1/2 of 1," 1 represents the whole, and the fraction 1/2 signifies one out of two equal parts of that whole.
Key Components of a Fraction:
- Numerator: The top number, indicating the number of parts being considered.
- Denominator: The bottom number, indicating the total number of equal parts the whole is divided into.
- Fraction Bar: The line separating the numerator and denominator, representing division.
The fraction 1/2 can also be visualized as a half, representing one of two equal parts. This visual representation helps solidify the understanding of the concept.
Calculating 1/2 of 1: A Step-by-Step Approach
The calculation of 1/2 of 1 involves a simple multiplication:
1/2 * 1 = 1/2
This demonstrates that half of one is, indeed, one-half or 0.5 in decimal form. The multiplication of a fraction and a whole number involves multiplying the numerator of the fraction by the whole number and keeping the denominator the same. In this case:
(1 * 1) / 2 = 1/2
Beyond the Basics: Expanding the Concept
While the answer to "What is 1/2 of 1?" is straightforward, understanding the underlying principles allows us to tackle more complex fraction problems. This simple calculation forms the foundation for numerous mathematical operations, including:
- Multiplication of fractions: Understanding this basic principle allows for efficient calculation of more intricate fraction multiplications, such as (3/4) * (2/5).
- Division of fractions: The reciprocal of a fraction plays a crucial role in division, building upon the understanding of fraction manipulation.
- Addition and Subtraction of fractions: Finding a common denominator is essential for these operations, which relies on understanding the concept of equivalent fractions.
- Solving equations involving fractions: Fractions appear extensively in various mathematical equations and problems, requiring a thorough understanding of fractional arithmetic.
Practical Applications of Fractions: Real-World Examples
Fractions are not merely abstract mathematical concepts; they are indispensable tools in numerous real-world applications:
- Measurement: Fractions are used extensively in measurements, from inches and centimeters to cooking recipes and construction projects. Half a cup of flour, a quarter of an inch of wood, these are all common examples of fractions in everyday life.
- Sharing and Division: Fractions help us divide things fairly. If you have one pizza and want to share it equally among two people, each person receives 1/2 of the pizza.
- Finance: Fractions are essential in financial calculations, involving percentages, interest rates, and stock market analysis. Understanding fractions is crucial for understanding financial concepts and making informed decisions.
- Data Analysis: Fractions and percentages are vital in data analysis and representation, allowing for the clear interpretation of datasets and statistical information.
- Science and Engineering: Fractions play a significant role in scientific measurements, formulas, and engineering calculations, ensuring precision and accuracy in various fields.
Addressing Common Misconceptions About Fractions
Several common misconceptions surround fractions, which can lead to errors in calculations and misunderstandings of the concepts:
- Confusing the numerator and denominator: Incorrectly identifying the numerator and denominator can lead to significant calculation errors. Remembering that the denominator represents the total parts and the numerator the parts being considered is crucial.
- Difficulty finding a common denominator: Adding or subtracting fractions requires finding a common denominator. Understanding least common multiples is essential for efficient fraction calculations.
- Incorrect simplification of fractions: Simplifying fractions involves reducing them to their simplest form. Incorrect simplification leads to inaccurate results.
- Misunderstanding the concept of equivalent fractions: Equivalent fractions represent the same value but have different numerators and denominators. Understanding this concept is important for various fraction operations.
Frequently Asked Questions (FAQs)
Q: What is the difference between 1/2 and 0.5?
A: 1/2 and 0.5 are equivalent representations of the same value. 1/2 is the fractional representation, while 0.5 is the decimal representation. Both signify one-half.
Q: How do I convert a fraction to a decimal?
A: To convert a fraction to a decimal, divide the numerator by the denominator. For example, 1/2 = 1 ÷ 2 = 0.5.
Q: How do I convert a decimal to a fraction?
A: To convert a decimal to a fraction, express the decimal as a fraction with a denominator of a power of 10 (10, 100, 1000, etc.). Then simplify the fraction to its simplest form. For example, 0.5 = 5/10 = 1/2.
Q: Why are fractions important?
A: Fractions are essential because they allow us to represent parts of a whole accurately. This is crucial in many aspects of daily life, from measurement to finance and scientific calculations.
Conclusion: Embracing the Power of Fractions
The question, "What is 1/2 of 1?", while seemingly simple, serves as a gateway to understanding the fundamental principles of fractions. Mastering fraction operations is essential for success in mathematics and various fields. By understanding the concepts, recognizing common misconceptions, and applying the knowledge to real-world situations, we can fully appreciate the power and utility of fractions in our lives. It's not just about finding the answer; it's about understanding the why behind the calculation, and that opens a world of mathematical possibilities. The ability to confidently manipulate fractions unlocks a deeper comprehension of the numerical world around us.
Latest Posts
Latest Posts
-
What Is The Square 8
Sep 25, 2025
-
7 12 Into A Decimal
Sep 25, 2025
-
How Long Is 7 Miles
Sep 25, 2025
-
How Many Grams In Quarter
Sep 25, 2025
-
Plant Parts Of A Flower
Sep 25, 2025
Related Post
Thank you for visiting our website which covers about What Is 1/2 Of 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.