Square Root Of 3 Cubed
dulhadulhi
Sep 24, 2025 · 5 min read
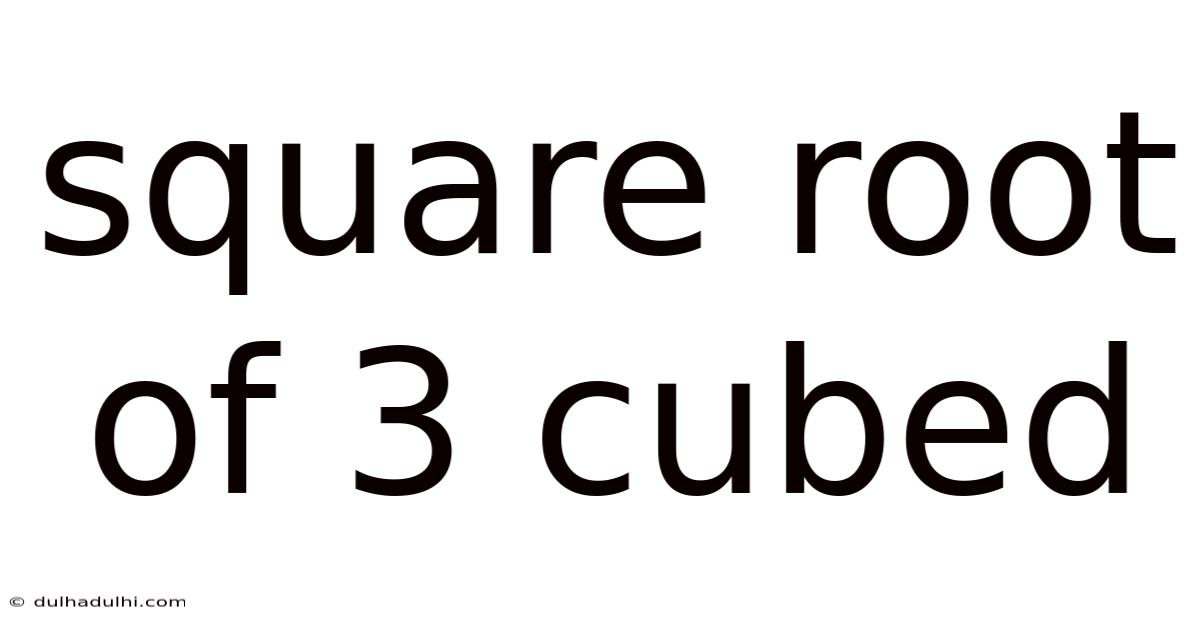
Table of Contents
Decoding the Mystery: A Deep Dive into the Cube of the Square Root of 3
The expression "square root of 3 cubed" might seem intimidating at first glance, but with a systematic approach, we can unravel its meaning and explore its mathematical significance. This article will dissect this mathematical concept, providing a clear understanding for both beginners and those seeking a deeper appreciation of its properties. We'll explore the calculation, delve into its geometric interpretations, and even examine its relevance in higher-level mathematics. By the end, you'll not only know the answer but also understand why the answer is what it is.
Understanding the Basics: Roots, Powers, and Order of Operations
Before tackling the cube of the square root of 3, let's refresh our understanding of fundamental mathematical concepts:
- Square Root: The square root of a number (√x) is a value that, when multiplied by itself, equals the original number (x). For example, √9 = 3 because 3 x 3 = 9.
- Cube: Cubing a number (x³) means multiplying the number by itself three times (x * x * x). For instance, 2³ = 2 x 2 x 2 = 8.
- Order of Operations (PEMDAS/BODMAS): Remember the acronym PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction) or BODMAS (Brackets, Orders, Division and Multiplication, Addition and Subtraction). This dictates the order in which we perform calculations. Exponents (or orders) are evaluated before multiplication or division.
Calculating the Cube of the Square Root of 3
Now, let's apply these principles to our expression: the cube of the square root of 3, which can be written mathematically as (√3)³.
Following the order of operations, we first address the square root:
-
Find the square root of 3: This is an irrational number, meaning it cannot be expressed as a simple fraction. Its approximate value is 1.732. However, for the sake of clarity and to show the process, we will leave it as √3 for now.
-
Cube the result: Now we cube the square root of 3: (√3)³ = √3 * √3 * √3.
This simplifies remarkably. Recall that √3 * √3 = 3 (because the square root and squaring operations cancel each other out). Therefore:
(√3)³ = 3 * √3 ≈ 3 * 1.732 ≈ 5.196
Therefore, the cube of the square root of 3 is 3√3. Its approximate decimal value is 5.196.
Geometric Interpretation: Visualizing the Cube
Mathematics often benefits from visualization. Let's consider a geometric interpretation of (√3)³. While directly representing the cube of a square root geometrically is complex, we can think about it in terms of volume.
Imagine a cube with sides of length √3. The volume of this cube would be (√3)³. This volume is equivalent to 3√3 cubic units. We can consider this volume to be composed of three smaller cubes each having a volume of √3 units cubed.
Exploring Further: Connections to Other Mathematical Concepts
The expression (√3)³ is not merely a simple calculation; it connects to several broader mathematical concepts:
-
Irrational Numbers: The square root of 3 is an irrational number, meaning it cannot be expressed as a fraction of two integers. Understanding this expression helps us grasp the properties of irrational numbers and how they behave within mathematical operations.
-
Radicals and Exponents: This example provides a practical application of working with radicals (square roots) and exponents (cubing). It reinforces the rules of manipulating these mathematical concepts.
-
Higher-Dimensional Geometry: As mentioned earlier, the geometric interpretation extends beyond a simple cube. The concept can be used to explain volumes and surface areas of higher-dimensional geometric shapes, especially those involving irrational numbers as side lengths.
-
Trigonometry: The square root of 3 plays a significant role in trigonometry. It frequently appears in calculations related to angles of 30°, 60°, and 90° within right-angled triangles. The understanding of (√3)³ can strengthen our overall understanding of trigonometric functions and their applications.
Frequently Asked Questions (FAQ)
Q1: Can I use a calculator to solve this?
A1: Yes, absolutely! Most scientific calculators can handle these calculations directly. Inputting "(1.732)^3" will give you an approximate answer. However, remember that 1.732 is just an approximation of √3. Therefore, the result will also be an approximation. It’s crucial to understand the underlying principles beyond just obtaining a numerical solution.
Q2: Is there a simpler way to express 3√3?
A2: While 3√3 is already a relatively simplified form, you could express it as a decimal approximation (approximately 5.196). However, the exact form, 3√3, is preferred in most mathematical contexts as it avoids rounding errors.
Q3: What if the expression were (√3)⁴?
A3: Following the same logic, (√3)⁴ = (√3)² * (√3)² = 3 * 3 = 9. The even exponent allows for complete cancellation of the square root.
Q4: What are some real-world applications of this concept?
A4: The square root of 3, and consequently expressions like (√3)³, appears in various real-world applications involving geometry and physics. For example, it's involved in calculating the diagonal of a cube, analyzing certain crystal structures, and solving problems related to vectors and forces in three-dimensional space. The precise applications are numerous and often depend on the specific context.
Conclusion: Beyond the Calculation
The cube of the square root of 3, (√3)³, is more than just a numerical answer; it's a stepping stone to a deeper understanding of mathematical concepts. By exploring this seemingly simple expression, we've encountered irrational numbers, honed our skills with radicals and exponents, and glimpsed its connection to geometry and even trigonometry. The journey of understanding this concept serves as a microcosm of the broader mathematical world—a world where seemingly simple expressions can unlock profound insights and connections. Remember that mastering mathematics often requires not only understanding the "how" but also the "why," allowing you to appreciate the elegance and interconnectedness of mathematical principles. This journey from a simple expression to a deeper appreciation of mathematical concepts demonstrates the rewarding nature of exploring mathematical ideas.
Latest Posts
Latest Posts
-
What Are Loci In Genetics
Sep 24, 2025
-
Area Of Parallelogram In Vectors
Sep 24, 2025
-
Kalahari Desert Location On Map
Sep 24, 2025
-
Is Gold A Good Conductor
Sep 24, 2025
-
Average Running Speed For Humans
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about Square Root Of 3 Cubed . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.