Solve 2 X 3 8
dulhadulhi
Sep 21, 2025 · 6 min read
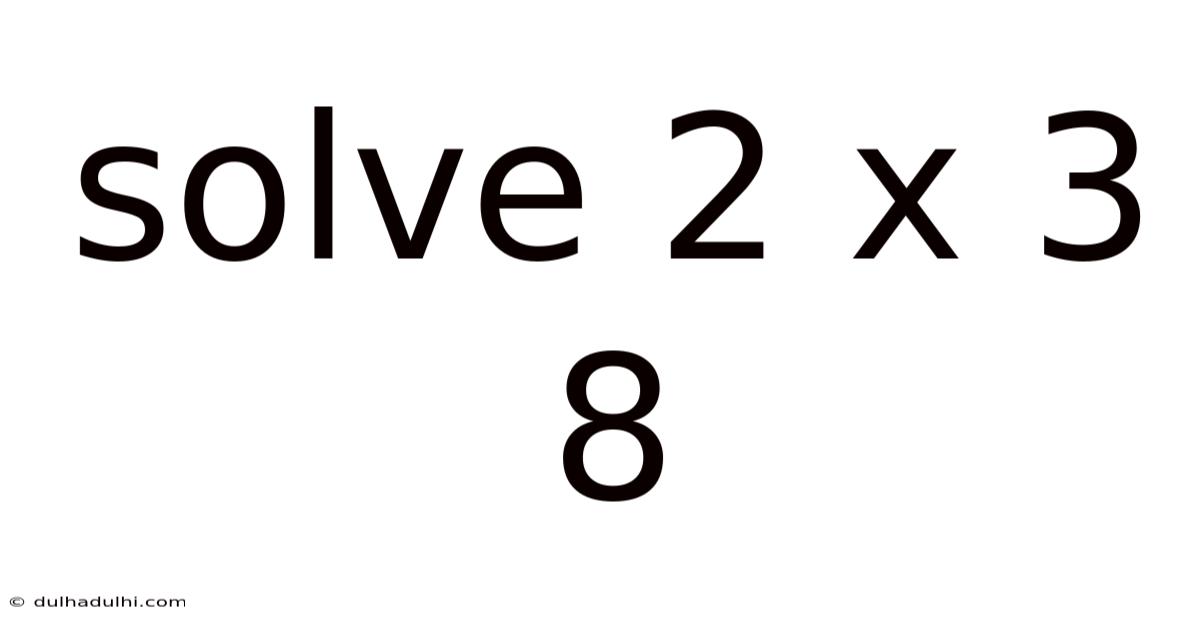
Table of Contents
Decoding the Puzzle: Solving "2 x 3 = 8" and Exploring Mathematical Thinking
The seemingly simple equation "2 x 3 = 8" is immediately recognizable as incorrect based on standard arithmetic. However, this isn't just a mistake; it's a puzzle, a prompt to think outside the box and explore different possibilities within mathematics. This article will delve into various approaches to "solving" this equation, examining different mathematical concepts and problem-solving strategies. We'll move beyond simple arithmetic and investigate how seemingly flawed statements can lead to rich learning experiences about abstract thinking and mathematical creativity.
Understanding the Problem: Beyond Standard Arithmetic
The statement "2 x 3 = 8" is clearly false within the context of standard base-10 arithmetic. We all know that 2 multiplied by 3 equals 6. So, what's going on? The key is to recognize that the puzzle challenges us to explore alternative interpretations and systems. This opens up a fascinating journey into unconventional mathematical thinking.
Possible Solutions and Interpretations
Several approaches can be used to make "2 x 3 = 8" a true statement, depending on how we reinterpret the symbols and operations involved. Let's explore some of them:
1. Altering the Operational System:
The most straightforward way to "solve" this is to consider alternative arithmetic systems. We're used to base-10 arithmetic, but other bases exist. While unlikely to directly produce 8, investigating different bases highlights the arbitrary nature of our familiar number system.
-
Base-n systems: In a base-n system, the digits used range from 0 to n-1. For instance, in base-2 (binary), only 0 and 1 are used. In base-16 (hexadecimal), digits from 0-9 and A-F (representing 10-15) are used. Exploring different bases helps us appreciate that numbers themselves are representations, not inherent properties. While this won't directly yield "2 x 3 = 8" in a simple substitution, understanding how different bases work is crucial to advanced mathematical concepts.
-
Modular Arithmetic: This involves working within a fixed set of numbers where we consider only the remainder after division by a specific number (the modulus). For example, in modulo 2 (mod 2), any even number is considered 0 and any odd number is considered 1. This system has interesting properties. Although it doesn't directly lead to 2 x 3 = 8, exploring modulo arithmetic provides insight into number theory and abstract algebra.
2. Redefining the Operators:
Instead of changing the base or system, we can alter the meaning of the multiplication operator itself. This requires defining a new operation that behaves differently than standard multiplication. Consider these possibilities:
-
Custom Operations: We could define a new binary operation, say "⊗", such that a ⊗ b = (a + b) + a. In this case, 2 ⊗ 3 = (2 + 3) + 2 = 7, which is still not 8, but illustrates the concept. Creating and defining our own mathematical operations teaches us about the flexibility and power of mathematical language.
-
Adding a Constant: We could subtly change the equation by including a hidden constant. For example, if we introduce a constant 'c' such that 2 x 3 + c = 8, then c = 2. This changes the equation but shows how an extra element can lead to a different result, highlighting the importance of explicitly defining all elements in an equation.
3. Geometric or Visual Interpretations:
Stepping away from purely numerical approaches, let's think geometrically. The numbers 2, 3, and 8 could represent different dimensions or properties of a shape:
-
Area and Perimeter: Imagine a rectangle with sides 2 and 3. Its area is 6, but perhaps the puzzle concerns the perimeter (2 + 2 + 3 + 3 = 10) or a combination of area and perimeter elements. We can design a unique shape where some measure yields 8. This demonstrates the link between arithmetic and geometry.
-
Visual Puzzles: The equation could represent a visual puzzle, where arranging two groups of three objects in a specific pattern results in a visual representation related to 8. This demonstrates the broader application of mathematical thinking beyond purely numerical problems.
4. Introducing Non-Standard Symbols:
We could reinterpret the symbols themselves. It's essential to be explicit about what symbols represent. Perhaps 'x' doesn't represent multiplication in this case. It could be a differently defined operator, a concatenation of symbols or something else entirely. The possibilities are endless, demonstrating the crucial role of clear definition and notation.
The Importance of Defining the Problem
The key to successfully "solving" "2 x 3 = 8" is to acknowledge the ambiguity inherent in the original statement. It lacks context, and it is the lack of context that allows for these various interpretations. The most crucial aspect of solving mathematical problems, especially unconventional ones, is clearly defining the scope, the rules, and the symbols involved.
Extending Mathematical Thinking: Beyond the Solution
While we've explored several approaches to interpret or modify the equation to make it true, the value extends beyond finding a solution. This puzzle serves as an excellent tool to:
- Promote Creative Problem Solving: It encourages thinking outside of the confines of standard arithmetic and exploring unconventional solutions.
- Develop Abstract Thinking: Understanding different mathematical systems and reinterpreting operations fosters abstract thinking skills.
- Illustrate Mathematical Flexibility: The puzzle demonstrates that mathematics isn't a rigid set of rules but a flexible and creative field.
- Enhance Number Sense: By exploring different number bases and operations, students improve their understanding of fundamental mathematical concepts.
- Improve Critical Thinking: The need to define terms and assumptions encourages critical evaluation of mathematical statements.
Frequently Asked Questions (FAQ)
Q: Is there one right answer to this puzzle?
A: No, there is no single "correct" answer. The value of the puzzle lies in the exploration of different mathematical concepts and problem-solving strategies, not in finding a definitive solution.
Q: Why is this puzzle useful in education?
A: This kind of puzzle challenges students to move beyond rote memorization and engage in creative problem-solving, enhancing their critical thinking and mathematical flexibility.
Q: Can this puzzle be used for students of all levels?
A: Yes, the puzzle can be adapted for different age groups. Younger students might focus on the visual or geometric interpretations, while older students can explore more advanced mathematical systems.
Q: How can I adapt this puzzle for my classroom?
A: Present the equation as a challenge, encouraging students to brainstorm different approaches. Guide discussions about different number bases, modular arithmetic, or create your own custom operations.
Conclusion: Embracing Mathematical Creativity
The puzzle "2 x 3 = 8" isn't a mathematical error; it's a stimulating challenge. By exploring various interpretations and problem-solving techniques, we gain a deeper understanding of mathematical concepts, enhance our critical thinking skills, and cultivate mathematical creativity. The true value lies not in finding a single "correct" answer, but in the enriching journey of exploration and discovery that it provides. The puzzle serves as a powerful reminder that mathematics is not just about following rules but about exploring possibilities and engaging with the subject creatively. It encourages us to question assumptions, explore different perspectives, and appreciate the diverse and flexible nature of mathematical thinking. Therefore, embracing the ambiguity and exploring different solutions is at the heart of this puzzle's educational value.
Latest Posts
Latest Posts
-
How Long Is 96 Hours
Sep 22, 2025
-
Are Chromosomes Visible During Interphase
Sep 22, 2025
-
Premium Diesel Vs Regular Diesel
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about Solve 2 X 3 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.