Prime Factor Decomposition Of 285
dulhadulhi
Sep 24, 2025 · 6 min read
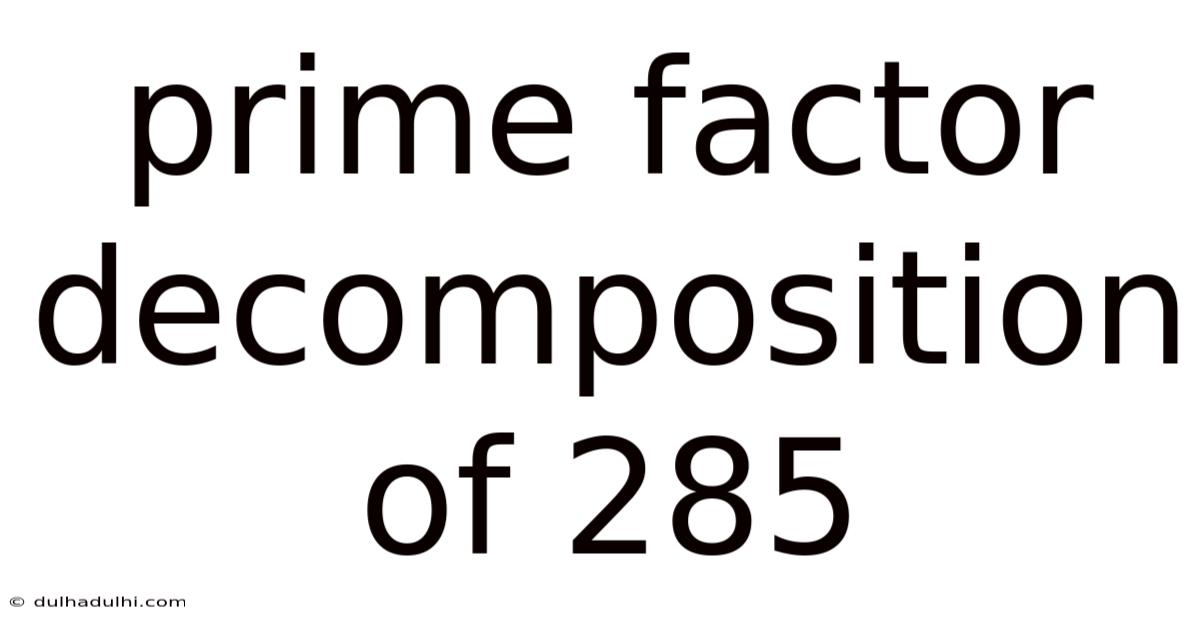
Table of Contents
Unveiling the Prime Building Blocks: A Deep Dive into the Prime Factorization of 285
Prime numbers, the fundamental building blocks of all whole numbers, hold a special place in mathematics. Understanding how to decompose a number into its prime factors is a crucial skill in various mathematical disciplines, from algebra to cryptography. This article will serve as a comprehensive guide to the prime factorization of 285, exploring the process step-by-step, explaining the underlying mathematical principles, and delving into the significance of prime factorization in broader mathematical contexts. We'll also tackle some frequently asked questions to solidify your understanding.
Introduction: What is Prime Factorization?
Prime factorization, also known as prime decomposition, is the process of finding the prime numbers that, when multiplied together, equal a given composite number (a whole number greater than 1 that is not prime). A prime number is a whole number greater than 1 that has only two divisors: 1 and itself. Examples of prime numbers include 2, 3, 5, 7, 11, and so on. Understanding prime factorization is crucial for simplifying fractions, solving algebraic equations, and grasping more advanced mathematical concepts. Let's embark on the journey of factoring 285 into its prime components.
Step-by-Step Prime Factorization of 285
The process of prime factorization involves systematically dividing the given number by the smallest prime number possible until you're left with only prime numbers. Here's how we can factorize 285:
-
Start with the smallest prime number: The smallest prime number is 2. However, 285 is an odd number, so it's not divisible by 2.
-
Try the next prime number: The next prime number is 3. To check divisibility by 3, we can sum the digits of 285 (2 + 8 + 5 = 15). Since 15 is divisible by 3, 285 is also divisible by 3.
-
Perform the division: 285 ÷ 3 = 95.
-
Continue the process: Now we need to factorize 95. 95 is not divisible by 3 (9 + 5 = 14, which is not divisible by 3). It's also not divisible by 5. Let's try 5.
-
Another division: 95 ÷ 5 = 19.
-
The final prime factor: 19 is a prime number. We can't divide it further.
Therefore, the prime factorization of 285 is 3 x 5 x 19. We've successfully broken down 285 into its fundamental prime constituents.
Visualizing the Prime Factorization: Factor Tree
A helpful visual aid for prime factorization is the factor tree. Let's create a factor tree for 285:
285
/ \
3 95
/ \
5 19
The factor tree shows the branching process of dividing the number until we reach only prime numbers at the end of each branch. The prime factors are 3, 5, and 19.
Mathematical Significance of Prime Factorization
The seemingly simple process of prime factorization has profound implications in various areas of mathematics:
-
Fundamental Theorem of Arithmetic: This theorem states that every integer greater than 1 can be represented uniquely as a product of prime numbers, disregarding the order of the factors. This uniqueness is a cornerstone of number theory.
-
Simplifying Fractions: Prime factorization is essential for simplifying fractions to their lowest terms. By factoring both the numerator and denominator into their prime factors, we can cancel out common factors, resulting in a simplified fraction. For instance, if we had the fraction 285/45, we could use prime factorization (285 = 3 x 5 x 19; 45 = 3 x 3 x 5) to simplify it to 19/3.
-
Greatest Common Divisor (GCD) and Least Common Multiple (LCM): Prime factorization provides an efficient method for finding the greatest common divisor (the largest number that divides both numbers without leaving a remainder) and the least common multiple (the smallest number that is a multiple of both numbers). By comparing the prime factors of two numbers, we can easily determine their GCD and LCM.
-
Cryptography: Prime numbers are fundamental in modern cryptography, particularly in public-key cryptosystems like RSA. The security of these systems relies on the difficulty of factoring extremely large numbers into their prime factors.
-
Algebra and Number Theory: Prime factorization plays a vital role in various areas of higher mathematics, including number theory, abstract algebra, and algebraic number theory. Understanding prime factorization provides a foundation for exploring more complex mathematical structures and relationships.
Exploring Further: The Uniqueness of Prime Factorization
The Fundamental Theorem of Arithmetic guarantees that the prime factorization of any number is unique, except for the order of the factors. For instance, 3 x 5 x 19 is the same as 5 x 3 x 19 or 19 x 5 x 3. This uniqueness is a critical aspect of number theory and allows us to work confidently with prime factorizations in various mathematical problems. The uniqueness ensures consistency and predictability in calculations.
Frequently Asked Questions (FAQ)
-
Q: Is there only one way to find the prime factorization of a number?
A: While there might be different approaches (like using a factor tree or repeated division), the final result – the set of prime factors – will always be the same, thanks to the Fundamental Theorem of Arithmetic.
-
Q: How can I quickly check if a number is divisible by 3?
A: Add up the digits of the number. If the sum is divisible by 3, the original number is also divisible by 3.
-
Q: What is the significance of prime factorization in real-world applications?
A: Beyond mathematics, prime factorization is crucial in cryptography, ensuring the security of online transactions and data protection. It's also used in coding and algorithm design.
-
Q: How can I practice prime factorization?
A: Start with smaller numbers and gradually increase the difficulty. Use factor trees and repeated division to find the prime factors. Online resources and practice exercises can also greatly help.
-
Q: What if I get stuck during the factorization process?
A: If you're unsure whether a number is prime, systematically check its divisibility by prime numbers, starting with the smallest ones (2, 3, 5, 7, 11, etc.). Use a prime number list or calculator as a helpful guide.
Conclusion: The Enduring Power of Prime Numbers
In conclusion, the prime factorization of 285, which is 3 x 5 x 19, is more than just a simple mathematical exercise. It illustrates the fundamental nature of prime numbers as the building blocks of all whole numbers. Understanding the process of prime factorization opens doors to a deeper appreciation of number theory and its applications in various fields, from simplifying fractions to securing online communications. The seemingly simple act of decomposing a number into its prime factors reveals a profound mathematical truth with far-reaching consequences. The journey of exploring prime factorization is a journey into the heart of mathematics itself, revealing the elegance and power hidden within seemingly simple concepts. So, keep exploring, keep questioning, and keep discovering the wonders of prime numbers!
Latest Posts
Latest Posts
-
Prime Factor Tree For 30
Sep 24, 2025
-
How Hen Eggs Are Fertilized
Sep 24, 2025
-
What Is 75 Of 40
Sep 24, 2025
-
1 Meter 85 In Feet
Sep 24, 2025
-
Square Root Of 27 Simplified
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about Prime Factor Decomposition Of 285 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.