Lcm Of 6 And 7
dulhadulhi
Sep 20, 2025 · 6 min read
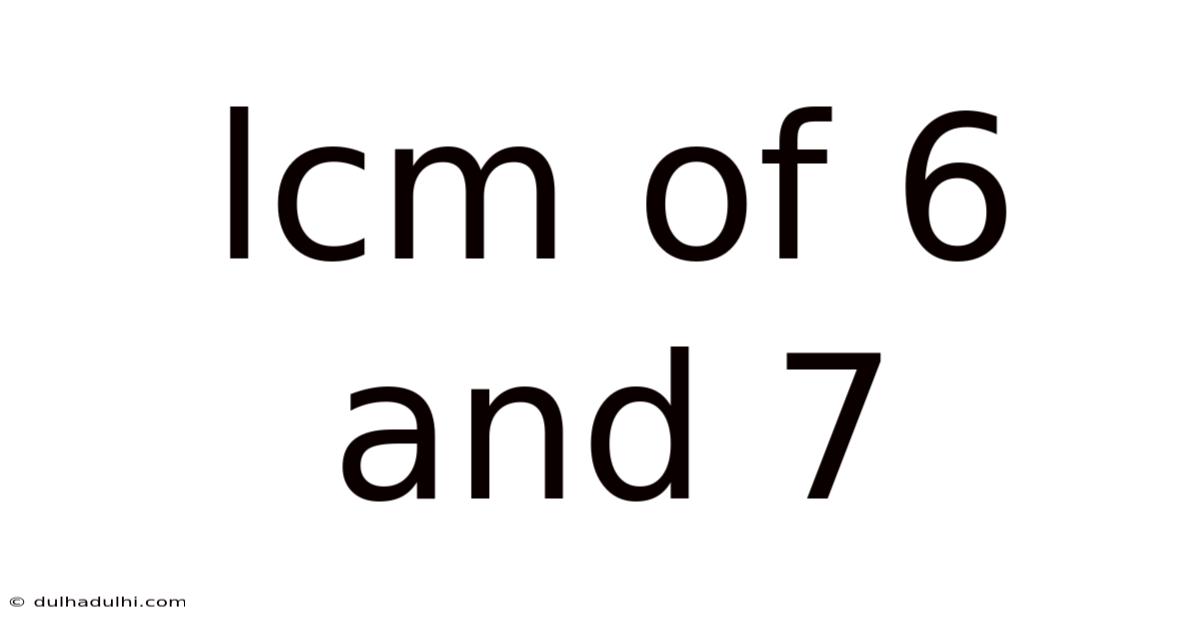
Table of Contents
Understanding the Least Common Multiple (LCM) of 6 and 7: A Deep Dive
Finding the least common multiple (LCM) might seem like a simple arithmetic task, but understanding the underlying concepts unlocks a deeper appreciation for number theory and its applications. This article delves into calculating the LCM of 6 and 7, explaining the various methods, and exploring the broader significance of LCMs in mathematics and beyond. We'll cover the basics, explore advanced techniques, and even address frequently asked questions to ensure a comprehensive understanding.
What is the Least Common Multiple (LCM)?
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers. In simpler terms, it's the smallest number that all the given numbers can divide into evenly. For example, the LCM of 2 and 3 is 6 because 6 is the smallest number that is divisible by both 2 and 3.
This concept is crucial in various mathematical fields and real-world applications, from simplifying fractions to scheduling events with recurring intervals.
Calculating the LCM of 6 and 7: Different Approaches
While the LCM of 6 and 7 might seem straightforward, let's explore different methods to understand the underlying principles. This will build a strong foundation for calculating LCMs of larger and more complex numbers.
1. Listing Multiples Method:
This is the most intuitive method, particularly for smaller numbers. We list the multiples of each number until we find the smallest multiple common to both.
- Multiples of 6: 6, 12, 18, 24, 30, 36, 42, 48, ...
- Multiples of 7: 7, 14, 21, 28, 35, 42, 49, ...
Notice that the smallest number appearing in both lists is 42. Therefore, the LCM of 6 and 7 is 42.
2. Prime Factorization Method:
This method is more efficient for larger numbers and provides a deeper understanding of the fundamental building blocks of numbers. It leverages the prime factorization of each number.
- Prime factorization of 6: 2 x 3
- Prime factorization of 7: 7 (7 is a prime number)
To find the LCM using prime factorization, we identify the highest power of each prime factor present in the factorizations:
- The prime factors are 2, 3, and 7.
- The highest power of 2 is 2<sup>1</sup> = 2
- The highest power of 3 is 3<sup>1</sup> = 3
- The highest power of 7 is 7<sup>1</sup> = 7
Multiply these highest powers together: 2 x 3 x 7 = 42. Therefore, the LCM of 6 and 7 is 42.
3. Greatest Common Divisor (GCD) Method:
The LCM and GCD (greatest common divisor) are closely related. There's a formula connecting them:
LCM(a, b) x GCD(a, b) = a x b
First, we find the GCD of 6 and 7 using the Euclidean algorithm or prime factorization. The GCD of 6 and 7 is 1 because they share no common factors other than 1.
Then, we apply the formula:
LCM(6, 7) x GCD(6, 7) = 6 x 7 LCM(6, 7) x 1 = 42 LCM(6, 7) = 42
This method highlights the interconnectedness between LCM and GCD, offering another perspective on the calculation.
The Significance of LCMs: Beyond Basic Arithmetic
The seemingly simple concept of LCM has far-reaching implications in various areas of mathematics and beyond:
-
Fraction Simplification: Finding the LCM of the denominators is crucial when adding or subtracting fractions. This allows us to find a common denominator, making the operation straightforward.
-
Scheduling and Time Management: Consider scenarios involving recurring events. If one event happens every 6 days and another every 7 days, the LCM (42) determines when both events will coincide again. This is essential in project management, logistics, and even daily life scheduling.
-
Modular Arithmetic: LCM plays a vital role in modular arithmetic, a branch of number theory with applications in cryptography and computer science. The concept of congruence modulo n relies heavily on the understanding of LCMs.
-
Music Theory: The LCM is used to determine the least common period of musical rhythms, ensuring harmonious combinations of different rhythmic patterns.
-
Construction and Engineering: LCM is used in various engineering applications, particularly in situations where synchronization and periodicity are crucial, such as in the design of gears, timing belts, and other mechanical systems.
Advanced LCM Calculations: More than Two Numbers
The methods described above can be extended to find the LCM of more than two numbers. For example, to find the LCM of 6, 7, and 10:
1. Prime Factorization Method (for multiple numbers):
- Prime factorization of 6: 2 x 3
- Prime factorization of 7: 7
- Prime factorization of 10: 2 x 5
Identify the highest power of each prime factor:
- 2<sup>1</sup> = 2
- 3<sup>1</sup> = 3
- 5<sup>1</sup> = 5
- 7<sup>1</sup> = 7
Multiply these together: 2 x 3 x 5 x 7 = 210. Therefore, the LCM of 6, 7, and 10 is 210.
2. Iterative Approach:
For multiple numbers, you can iteratively calculate the LCM. Find the LCM of the first two numbers, then find the LCM of that result and the third number, and so on.
For example, for 6, 7, and 10:
- LCM(6, 7) = 42
- LCM(42, 10) = 210
Frequently Asked Questions (FAQ)
Q: What if the numbers have common factors?
A: The methods described above, especially prime factorization, automatically handle numbers with common factors. The prime factorization method ensures that you only consider the highest power of each prime factor, effectively eliminating redundancy caused by common factors.
Q: Is there a formula for LCM for more than two numbers?
A: There isn't a single compact formula like the one relating LCM and GCD for two numbers. However, the methods described – prime factorization and the iterative approach – effectively handle LCM calculations for any number of integers.
Q: Can the LCM be larger than the largest number?
A: Yes, absolutely. The LCM is only equal to the largest number if the largest number is a multiple of all the other numbers. In most cases, the LCM will be larger or equal to the largest number in the set.
Q: What if one of the numbers is 0?
A: The LCM of any set of numbers including 0 is undefined. Zero has an infinite number of multiples, making it impossible to find the least common multiple.
Q: Are there any online LCM calculators?
A: Yes, many online calculators can compute the LCM of numbers. These are useful for checking your work or calculating LCMs of very large numbers. However, understanding the underlying methods is crucial for a deeper understanding of mathematics.
Conclusion
Understanding the least common multiple goes beyond simple arithmetic calculations. It's a fundamental concept with far-reaching applications across various disciplines. Mastering different methods of calculating LCMs, from listing multiples to using prime factorization and the GCD method, provides a stronger foundation in number theory and its applications in real-world problems. While the LCM of 6 and 7, being 42, might seem like a small step, it represents a significant building block in understanding a much larger mathematical landscape. The principles discussed here provide a solid foundation for tackling more complex problems involving LCMs and related concepts. Remember that the key is not just to find the answer but to understand the 'why' behind the calculation, deepening your mathematical intuition and problem-solving skills.
Latest Posts
Latest Posts
-
What Is The Suffix Name
Sep 20, 2025
-
Does Chewing Gum Help Nausea
Sep 20, 2025
-
Rate Of Flow Of Charge
Sep 20, 2025
-
50 1 Gas Oil Mixture
Sep 20, 2025
-
Blonde Hair On Brown Eyes
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 6 And 7 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.