Lcm Of 40 And 220
dulhadulhi
Sep 23, 2025 · 6 min read
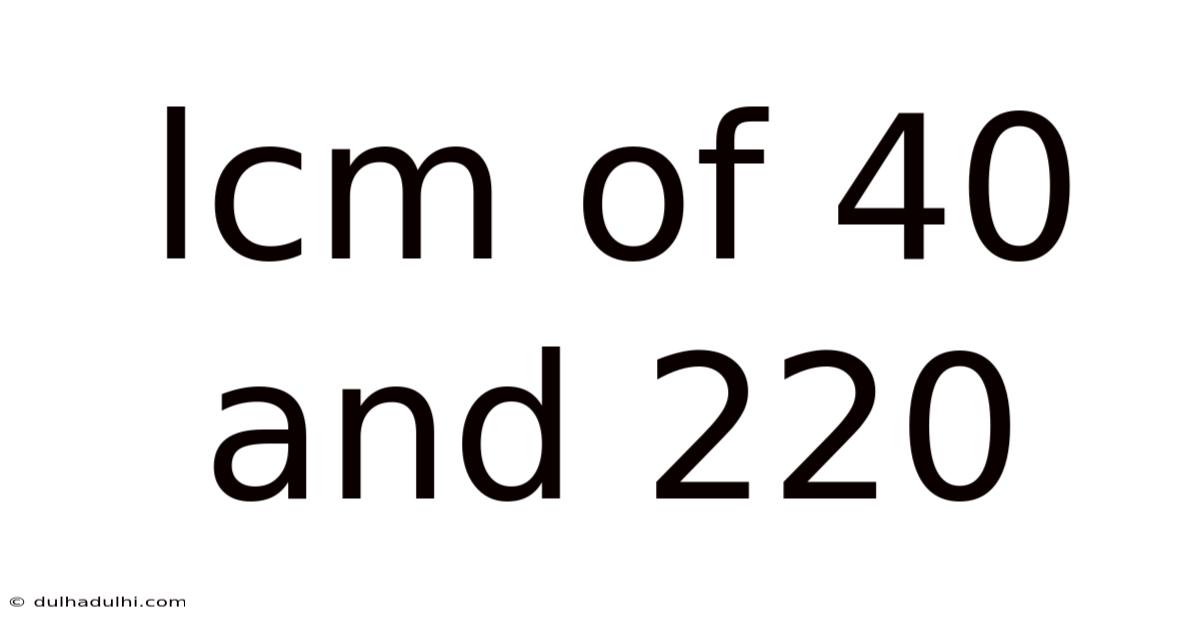
Table of Contents
Finding the Least Common Multiple (LCM) of 40 and 220: A Comprehensive Guide
Finding the least common multiple (LCM) might seem like a simple arithmetic task, but understanding the underlying principles and different methods can significantly enhance your mathematical skills and problem-solving abilities. This comprehensive guide dives deep into calculating the LCM of 40 and 220, exploring various approaches, explaining the theoretical background, and addressing frequently asked questions. Whether you're a student brushing up on your math skills or an educator seeking clear explanations, this article will provide a thorough understanding of LCM and its application.
Understanding Least Common Multiple (LCM)
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers. Think of it as the smallest number that contains all the numbers in your set as factors. For instance, if we're looking at the LCM of 2 and 3, the answer is 6 because 6 is the smallest number divisible by both 2 and 3. Understanding the LCM is crucial in various mathematical applications, including simplifying fractions, solving problems involving time and distance, and even in more advanced areas like abstract algebra.
Methods for Finding the LCM of 40 and 220
Several methods can be employed to determine the LCM of 40 and 220. Let's explore the most common and efficient approaches:
1. Listing Multiples Method:
This method involves listing the multiples of both numbers until a common multiple is found. While straightforward for smaller numbers, it can become tedious for larger numbers.
- Multiples of 40: 40, 80, 120, 160, 200, 240, 280, 320, 360, 400, 440, 480...
- Multiples of 220: 220, 440, 660, 880...
The smallest common multiple in both lists is 440. Therefore, the LCM of 40 and 220 using this method is 440.
2. Prime Factorization Method:
This method is generally more efficient, especially for larger numbers. It involves finding the prime factorization of each number and then constructing the LCM using the highest powers of all the prime factors present.
- Prime factorization of 40: 2³ x 5
- Prime factorization of 220: 2² x 5 x 11
To find the LCM, we take the highest power of each prime factor present in either factorization:
- Highest power of 2: 2³ = 8
- Highest power of 5: 5¹ = 5
- Highest power of 11: 11¹ = 11
Multiplying these together: 8 x 5 x 11 = 440. Therefore, the LCM of 40 and 220 using prime factorization is 440.
3. Greatest Common Divisor (GCD) Method:
This method utilizes the relationship between the LCM and the greatest common divisor (GCD) of two numbers. The formula is:
LCM(a, b) = (|a x b|) / GCD(a, b)
First, we need to find the GCD of 40 and 220. We can use the Euclidean algorithm for this:
- Divide the larger number (220) by the smaller number (40): 220 ÷ 40 = 5 with a remainder of 20.
- Replace the larger number with the smaller number (40) and the smaller number with the remainder (20): 40 ÷ 20 = 2 with a remainder of 0.
- Since the remainder is 0, the GCD is the last non-zero remainder, which is 20.
Now, we can apply the formula:
LCM(40, 220) = (40 x 220) / 20 = 8800 / 20 = 440
Therefore, the LCM of 40 and 220 using the GCD method is 440.
A Deeper Dive into Prime Factorization
The prime factorization method offers a powerful and systematic approach to finding the LCM. Let's break down why it works so effectively:
-
Prime Numbers: A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself (e.g., 2, 3, 5, 7, 11...). Prime numbers are the building blocks of all other integers.
-
Unique Factorization Theorem: The fundamental theorem of arithmetic (also known as the unique factorization theorem) states that every integer greater than 1 can be represented uniquely as a product of prime numbers, up to the order of the factors. This is the cornerstone of the prime factorization method for finding the LCM.
By breaking down each number into its prime factors, we identify the essential components that contribute to their divisibility. The LCM then becomes a combination of these prime factors, ensuring divisibility by both original numbers. Taking the highest power of each prime factor guarantees that we are considering the smallest number that satisfies the condition of divisibility for both integers.
Applications of LCM
Understanding LCM extends beyond simple arithmetic exercises. It finds practical applications in various fields:
-
Scheduling: Determining when events will coincide. For example, if two buses depart from the same station at different intervals, the LCM helps determine when they will depart simultaneously again.
-
Fraction Operations: Finding the least common denominator (LCD) when adding or subtracting fractions. The LCD is simply the LCM of the denominators.
-
Measurement Conversions: Converting between different units of measurement often involves LCM.
-
Music Theory: LCM plays a role in determining the least common multiple of musical note durations and rhythm.
-
Computer Science: Algorithms in computer science often use the concept of LCM for tasks like scheduling and synchronization.
Frequently Asked Questions (FAQ)
Q1: What is the difference between LCM and GCD?
The Least Common Multiple (LCM) is the smallest number that is a multiple of both numbers. The Greatest Common Divisor (GCD), also known as the highest common factor (HCF), is the largest number that divides both numbers without leaving a remainder. They are inversely related, as shown in the formula: LCM(a, b) = (|a x b|) / GCD(a, b).
Q2: Can the LCM of two numbers be greater than the product of the two numbers?
No, the LCM of two numbers can never be greater than their product. The formula LCM(a, b) = (|a x b|) / GCD(a, b) demonstrates this. Since the GCD is always less than or equal to the smaller of the two numbers, the LCM will always be less than or equal to the product.
Q3: Is there a way to find the LCM of more than two numbers?
Yes, the prime factorization method extends seamlessly to multiple numbers. You find the prime factorization of each number, and then take the highest power of each prime factor present among all the numbers to construct the LCM.
Q4: Why is the prime factorization method preferred over the listing multiples method for larger numbers?
The listing multiples method becomes increasingly inefficient and time-consuming as numbers grow larger. The prime factorization method offers a more structured and efficient approach, especially when dealing with numbers that have many factors.
Conclusion
Finding the least common multiple (LCM) is a fundamental concept in mathematics with wide-ranging applications. While multiple methods exist, the prime factorization method provides a systematic and efficient approach, especially for larger numbers. Understanding the underlying principles of prime factorization and the relationship between LCM and GCD empowers you to tackle more complex mathematical problems with confidence. This comprehensive guide has explored various methods for calculating the LCM of 40 and 220, demonstrating the versatility and importance of this mathematical concept. Remember, mastering the LCM not only improves your mathematical proficiency but also equips you with essential problem-solving skills applicable across numerous disciplines.
Latest Posts
Latest Posts
-
What Is A Stratified Survey
Sep 23, 2025
-
Lock And Key Theory Enzymes
Sep 23, 2025
-
How Many Zeros In Quadrillion
Sep 23, 2025
-
Meaning Of Interval In Math
Sep 23, 2025
-
Is Displacement Scalar Or Vector
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 40 And 220 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.