Lcm Of 4 6 8
dulhadulhi
Sep 25, 2025 · 6 min read
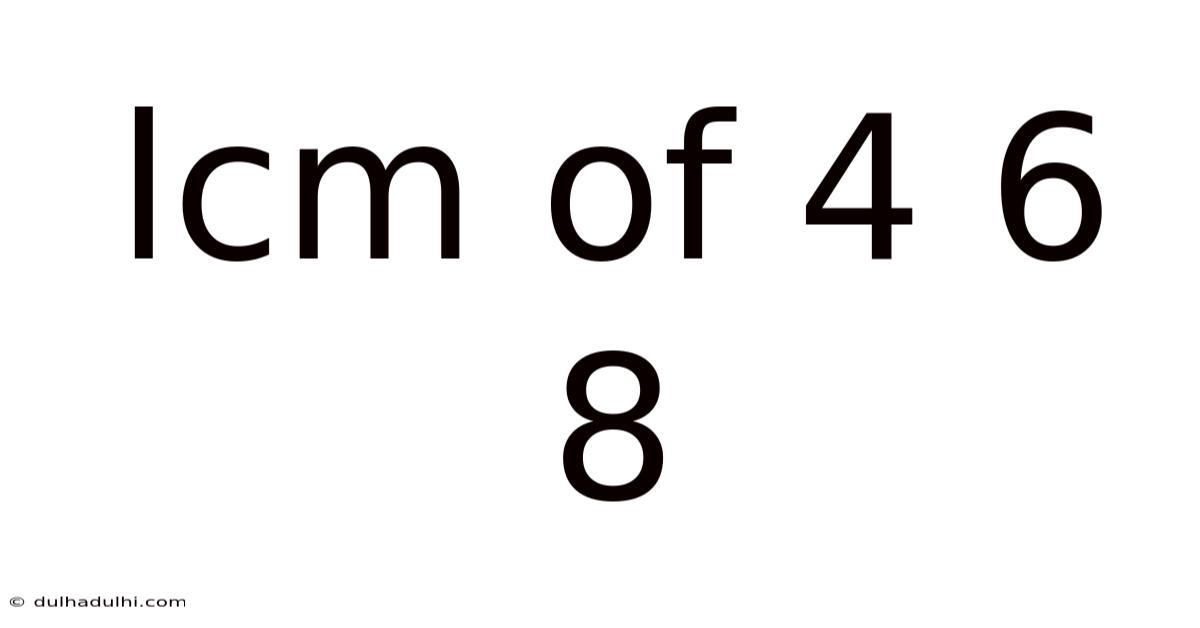
Table of Contents
Understanding the Least Common Multiple (LCM) of 4, 6, and 8
Finding the Least Common Multiple (LCM) might seem like a simple math problem, but understanding the concept behind it opens doors to more complex mathematical operations and real-world applications. This article will delve deep into calculating the LCM of 4, 6, and 8, exploring different methods and explaining the underlying principles. We’ll also explore why understanding LCM is crucial in various fields, from scheduling tasks to understanding rhythmic patterns in music.
Introduction to Least Common Multiple (LCM)
The Least Common Multiple (LCM) of a set of numbers is the smallest positive integer that is divisible by all the numbers in the set. In simpler terms, it's the smallest number that all the numbers in your set can divide into evenly. For example, if you want to find the LCM of 2 and 3, you'd look for the smallest number that both 2 and 3 can divide into without leaving a remainder. That number is 6.
Understanding the LCM is critical in various scenarios. For instance, if you're trying to schedule events that repeat at different intervals (like buses arriving every 4 minutes, 6 minutes, and 8 minutes), the LCM will tell you the soonest time when all events will coincide. This principle extends to numerous applications in engineering, music theory, and even computer science.
Methods for Finding the LCM of 4, 6, and 8
There are several ways to determine the LCM of 4, 6, and 8. Let's explore the most common methods:
1. Listing Multiples:
This is a straightforward approach, especially for smaller numbers. We list the multiples of each number until we find the smallest multiple common to all three:
- Multiples of 4: 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, 52, 56, 60...
- Multiples of 6: 6, 12, 18, 24, 30, 36, 42, 48, 54, 60...
- Multiples of 8: 8, 16, 24, 32, 40, 48, 56, 64, 72, 80...
By comparing the lists, we see that the smallest common multiple is 24. Therefore, the LCM(4, 6, 8) = 24. This method is effective for smaller numbers but becomes cumbersome as the numbers increase in size.
2. Prime Factorization Method:
This is a more efficient method for larger numbers. It involves finding the prime factors of each number and then constructing the LCM using these factors.
- Prime factorization of 4: 2 x 2 = 2²
- Prime factorization of 6: 2 x 3
- Prime factorization of 8: 2 x 2 x 2 = 2³
To find the LCM, we take the highest power of each prime factor present in the factorizations:
- The highest power of 2 is 2³ = 8
- The highest power of 3 is 3¹ = 3
Now, multiply these highest powers together: 8 x 3 = 24. Therefore, the LCM(4, 6, 8) = 24. This method is more systematic and efficient than listing multiples, particularly when dealing with larger numbers.
3. Greatest Common Divisor (GCD) Method:
The LCM and GCD (Greatest Common Divisor) are related. We can use the GCD to calculate the LCM using the following formula:
LCM(a, b, c) = (a x b x c) / GCD(a, b, c)
First, let's find the GCD of 4, 6, and 8 using the Euclidean algorithm or prime factorization. The GCD(4, 6, 8) = 2.
Now, apply the formula: LCM(4, 6, 8) = (4 x 6 x 8) / 2 = 192 / 2 = 24.
This method is also quite efficient, particularly when the GCD is easily calculable.
Explanation of the Prime Factorization Method in Detail
The prime factorization method provides a clear and structured way to find the LCM. Let's break it down further:
-
Find the prime factors: Express each number as a product of its prime factors. Remember, a prime number is a whole number greater than 1 that has only two divisors: 1 and itself (e.g., 2, 3, 5, 7, 11...).
-
Identify the highest powers: For each prime factor appearing in the factorizations, identify the highest power of that prime factor. For instance, if 2 appears as 2², 2¹, and 2³, the highest power is 2³.
-
Multiply the highest powers: Multiply the highest powers of all the distinct prime factors together. This product is the LCM.
This systematic approach eliminates the need for extensive listing of multiples, making it suitable for larger numbers and more complex scenarios involving multiple numbers.
Real-World Applications of LCM
The concept of LCM transcends the realm of abstract mathematics and finds practical applications in diverse fields:
-
Scheduling: Imagine planning a meeting with colleagues who are available every 4 days, 6 days, and 8 days. The LCM (24 days) tells you the earliest date when everyone will be simultaneously available.
-
Music: In music theory, the LCM helps determine the least common denominator for rhythmic patterns. Understanding LCMs is essential for composing and understanding musical harmony.
-
Engineering: In engineering projects, LCM helps synchronize repetitive actions or processes, ensuring optimal efficiency and timing.
-
Construction: When working with materials of different lengths, understanding LCM can aid in optimizing cutting and minimizing waste.
-
Computer Science: LCMs are used in various algorithms and processes within computer science, particularly those involving timing and synchronization.
Frequently Asked Questions (FAQ)
-
What is the difference between LCM and GCD? The LCM is the smallest multiple common to all numbers, while the GCD is the largest divisor common to all numbers. They are inversely related.
-
Can I use a calculator to find the LCM? Many calculators have built-in functions to calculate the LCM. However, understanding the underlying methods is crucial for grasping the concept and applying it to more complex problems.
-
What if the numbers have no common factors? If the numbers are relatively prime (meaning they share no common factors other than 1), their LCM will be the product of the numbers.
-
How can I improve my understanding of LCM? Practice! Solve various LCM problems using different methods to solidify your understanding.
Conclusion
The LCM of 4, 6, and 8 is 24. While seemingly a simple calculation, understanding the concept of the LCM and the various methods to find it is vital for broader mathematical comprehension and application in real-world contexts. The prime factorization method offers a robust and efficient approach, especially when dealing with larger numbers. Mastering the LCM enhances problem-solving skills across multiple disciplines, from scheduling and music theory to engineering and computer science. By understanding the fundamental principles and practicing different methods, you’ll not only be able to calculate LCMs effectively but also appreciate their significance in various facets of life. This detailed explanation should equip you with the knowledge and confidence to tackle more complex LCM problems and appreciate the power of this fundamental mathematical concept.
Latest Posts
Latest Posts
-
Surface Area For 3d Shapes
Sep 25, 2025
-
Difference In Lake And Pond
Sep 25, 2025
-
Joules To Kilowatts Per Hour
Sep 25, 2025
-
Is Nickel A Magnetic Material
Sep 25, 2025
-
Formula Of Gravitational Field Strength
Sep 25, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 4 6 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.