Lcm Of 36 And 16
dulhadulhi
Sep 25, 2025 · 6 min read
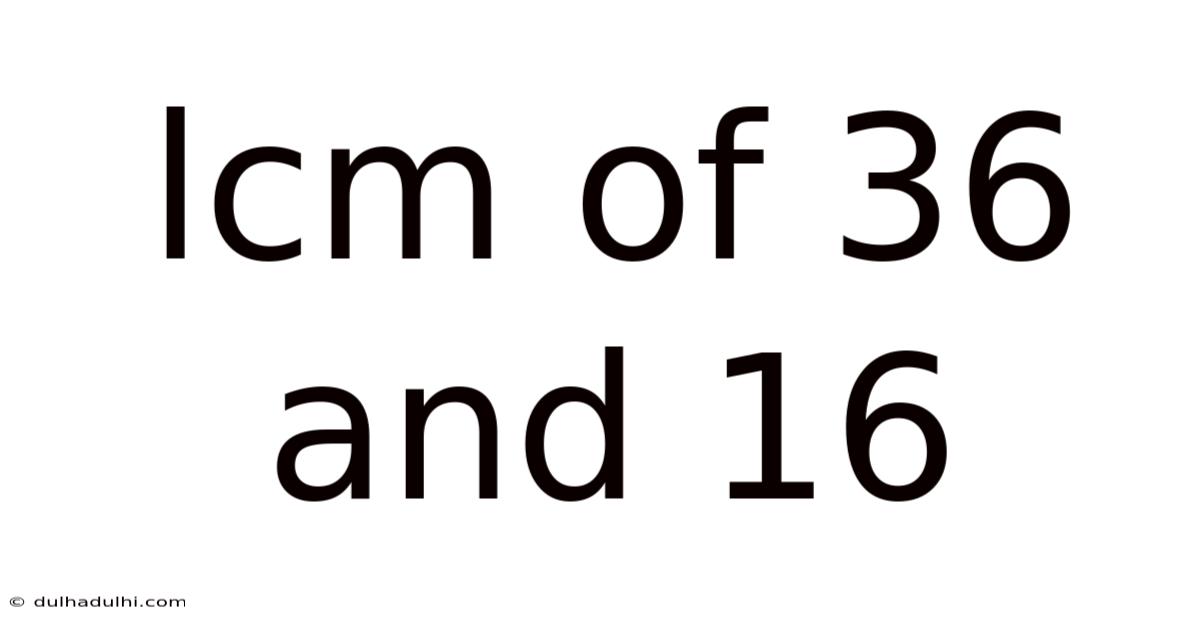
Table of Contents
Finding the LCM of 36 and 16: A Comprehensive Guide
Finding the least common multiple (LCM) of two numbers is a fundamental concept in mathematics, crucial for various applications ranging from simple fraction arithmetic to more complex problems in algebra and number theory. This article delves deep into the process of finding the LCM of 36 and 16, exploring different methods and providing a thorough understanding of the underlying principles. We'll move beyond a simple answer and explore the "why" behind the calculations, making this a valuable resource for students and anyone looking to solidify their understanding of LCM.
Introduction: What is LCM?
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the numbers. Understanding LCM is critical for simplifying fractions, solving problems involving cycles (like finding when two events will coincide), and working with ratios and proportions. In this article, we will focus on finding the LCM of 36 and 16, demonstrating several methods to achieve this. We will also explore the prime factorization method, which is a powerful technique applicable to finding the LCM of any set of integers.
Method 1: Listing Multiples
One of the simplest methods, though less efficient for larger numbers, is to list the multiples of each number until we find the smallest common multiple.
- Multiples of 36: 36, 72, 108, 144, 180, 216, 252, 288, 324, 360…
- Multiples of 16: 16, 32, 48, 64, 80, 96, 112, 128, 144, 160, 176, 192, 208, 224, 240, 256, 272, 288, 304, 320…
By comparing the lists, we can see that the smallest number appearing in both lists is 144. Therefore, the LCM of 36 and 16 is 144. This method is straightforward but can become cumbersome when dealing with larger numbers.
Method 2: Prime Factorization
This is a more efficient and systematic approach, especially when dealing with larger numbers or multiple numbers. It involves breaking down each number into its prime factors.
- Prime factorization of 36: 36 = 2² x 3² (2 x 2 x 3 x 3)
- Prime factorization of 16: 16 = 2⁴ (2 x 2 x 2 x 2)
To find the LCM using prime factorization:
- Identify all the prime factors present in both numbers. In this case, we have 2 and 3.
- For each prime factor, select the highest power that appears in either factorization. The highest power of 2 is 2⁴ (from 16), and the highest power of 3 is 3² (from 36).
- Multiply the selected highest powers together. LCM(36, 16) = 2⁴ x 3² = 16 x 9 = 144
Therefore, the LCM of 36 and 16 is 144. This method is significantly more efficient than listing multiples, especially when dealing with larger numbers with many prime factors.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and GCD (Greatest Common Divisor) of two numbers are closely related. There's a formula connecting them:
LCM(a, b) = (|a x b|) / GCD(a, b)
First, we need to find the GCD of 36 and 16. We can use the Euclidean algorithm for this:
- Divide the larger number (36) by the smaller number (16): 36 = 2 x 16 + 4
- Replace the larger number with the smaller number (16) and the smaller number with the remainder (4): 16 = 4 x 4 + 0
The last non-zero remainder is the GCD, which is 4.
Now, we can use the formula:
LCM(36, 16) = (36 x 16) / 4 = 576 / 4 = 144
This method provides an alternative way to calculate the LCM, leveraging the relationship between LCM and GCD. The Euclidean algorithm is particularly useful for finding the GCD of larger numbers efficiently.
Explanation of the Prime Factorization Method: A Deeper Dive
The prime factorization method is based on the fundamental theorem of arithmetic, which states that every integer greater than 1 can be represented uniquely as a product of prime numbers (ignoring the order of the factors). This uniqueness is key to understanding why this method works for finding the LCM.
When we find the prime factorization of each number, we are essentially breaking it down into its fundamental building blocks. The LCM must contain all these building blocks (prime factors) to be divisible by both original numbers. By selecting the highest power of each prime factor, we ensure that the resulting number is divisible by both numbers and is the smallest such number.
Applications of LCM:
Finding the LCM has various practical applications:
- Fraction Addition and Subtraction: To add or subtract fractions with different denominators, you need to find the LCM of the denominators to create a common denominator.
- Scheduling and Cycles: Imagine two events that occur at regular intervals. Finding the LCM of those intervals tells you when both events will occur simultaneously. For example, if one event happens every 36 days and another every 16 days, they will coincide again after 144 days.
- Gear Ratios and Mechanical Systems: LCM is used in engineering to determine gear ratios and synchronize the movements of different components in machinery.
- Music Theory: LCM helps determine the least common multiple of note durations and frequencies in musical composition.
- Computer Science: LCM finds applications in algorithms and scheduling processes within computer systems.
Frequently Asked Questions (FAQ)
-
What is the difference between LCM and GCD? The LCM is the smallest common multiple, while the GCD is the greatest common divisor. They are related through the formula: LCM(a, b) = (|a x b|) / GCD(a, b).
-
Can I use this method for more than two numbers? Yes, the prime factorization method extends easily to find the LCM of more than two numbers. You simply find the prime factorization of each number, select the highest power of each prime factor present, and multiply them together.
-
Why is the prime factorization method more efficient? The listing multiples method becomes extremely inefficient as numbers get larger. Prime factorization systematically breaks down the numbers into their fundamental components, making it a much more efficient and scalable approach.
-
What if the two numbers are relatively prime? If two numbers are relatively prime (meaning their GCD is 1), their LCM is simply their product.
Conclusion:
Finding the least common multiple (LCM) is a crucial skill in mathematics with broad applications. While listing multiples is a simple method for small numbers, the prime factorization method provides a more efficient and systematic approach, particularly useful for larger numbers. Understanding the relationship between LCM and GCD provides an alternative route to calculation. Mastering these techniques enhances your mathematical proficiency and opens the door to solving a wider array of problems in various fields. The LCM of 36 and 16, as demonstrated through multiple methods, is 144. This consistent result underscores the power and reliability of these mathematical principles. Remember to practice these methods to build a strong understanding and confidence in tackling LCM problems of any complexity.
Latest Posts
Latest Posts
-
What Is Locus In Biology
Sep 25, 2025
-
Translucent Vs Transparent Vs Opaque
Sep 25, 2025
-
Square Numbers Up To 200
Sep 25, 2025
-
Virus Structure A Level Biology
Sep 25, 2025
-
6000 Sq Feet To Meters
Sep 25, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 36 And 16 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.