Lcm Of 3 5 10
dulhadulhi
Sep 25, 2025 · 5 min read
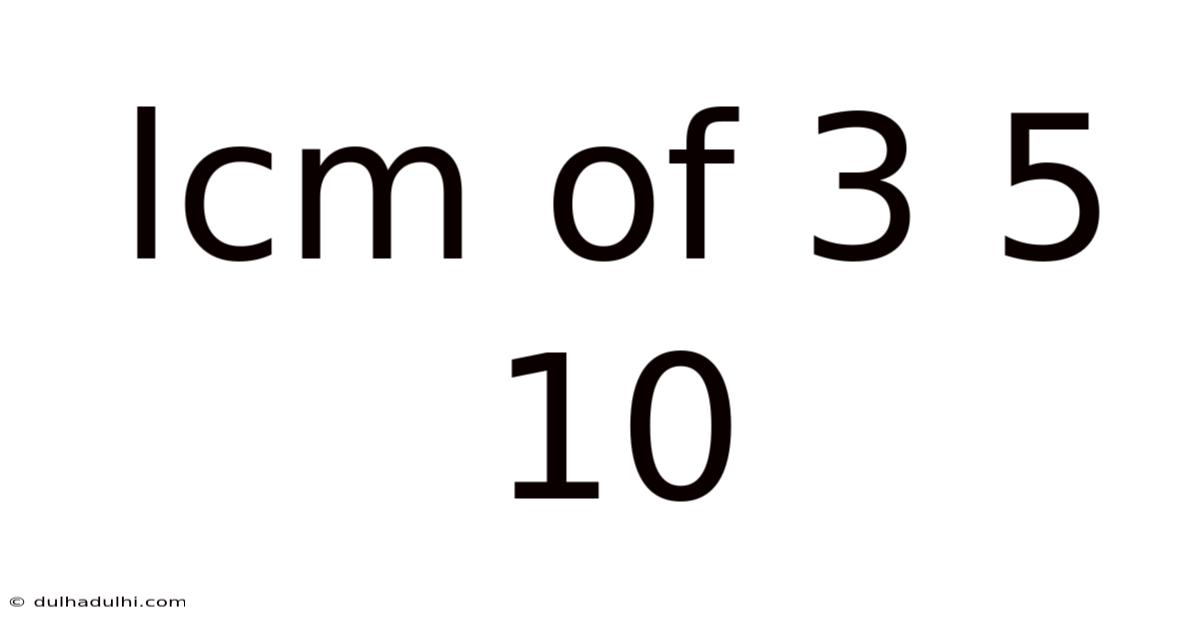
Table of Contents
Understanding the Least Common Multiple (LCM) of 3, 5, and 10
Finding the Least Common Multiple (LCM) is a fundamental concept in mathematics, crucial for various applications from simple fraction addition to complex scheduling problems. This article will delve deep into understanding the LCM, specifically focusing on finding the LCM of 3, 5, and 10. We'll explore different methods, explain the underlying principles, and provide examples to solidify your understanding. This comprehensive guide will leave you not only knowing the answer but also understanding why that answer is correct and how to tackle similar problems in the future.
What is the Least Common Multiple (LCM)?
The Least Common Multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers. In simpler terms, it's the smallest number that all the given numbers can divide into evenly without leaving a remainder. For example, the LCM of 2 and 3 is 6 because 6 is the smallest number that is divisible by both 2 and 3.
Method 1: Listing Multiples
The most straightforward method to find the LCM is by listing the multiples of each number until you find the smallest common multiple. Let's apply this to find the LCM of 3, 5, and 10:
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, ...
- Multiples of 5: 5, 10, 15, 20, 25, 30, 35, ...
- Multiples of 10: 10, 20, 30, 40, ...
By comparing the lists, we see that the smallest number present in all three lists is 30. Therefore, the LCM of 3, 5, and 10 is 30.
Method 2: Prime Factorization
This method is more efficient for larger numbers and provides a deeper understanding of the underlying mathematical principles. It involves finding the prime factorization of each number and then constructing the LCM from the highest powers of each prime factor.
Let's break down each number into its prime factors:
- 3 = 3 (3 is a prime number)
- 5 = 5 (5 is a prime number)
- 10 = 2 x 5
Now, we identify the unique prime factors present in these numbers: 2, 3, and 5. We take the highest power of each prime factor:
- Highest power of 2: 2¹ = 2
- Highest power of 3: 3¹ = 3
- Highest power of 5: 5¹ = 5
Finally, we multiply these highest powers together: 2 x 3 x 5 = 30. Therefore, the LCM of 3, 5, and 10 is again 30.
Method 3: Greatest Common Divisor (GCD) Method
The LCM and GCD (Greatest Common Divisor) are closely related. There's a formula that connects them:
LCM(a, b) * GCD(a, b) = a * b
While this formula is generally used for two numbers, we can extend it to multiple numbers by finding the LCM iteratively. First, let's find the GCD of 3, 5, and 10. Since 3 and 5 are prime numbers and 10 is 2 x 5, the GCD of 3, 5, and 10 is 1.
Now let's use the LCM of two numbers at a time.
- LCM (3, 5) = 15 (because 3 and 5 have no common factors except 1)
- LCM (15, 10) = 30 (15 = 3 x 5 and 10 = 2 x 5, so LCM is 2 x 3 x 5 = 30)
Therefore, the LCM of 3, 5, and 10 is 30.
Understanding the Concept of Divisibility
The key to understanding LCM lies in the concept of divisibility. A number 'a' is divisible by another number 'b' if the remainder is 0 when 'a' is divided by 'b'. The LCM is the smallest number that satisfies this divisibility condition for all the given numbers. In our example, 30 is divisible by 3, 5, and 10 without leaving any remainder.
Real-world Applications of LCM
The LCM is not just an abstract mathematical concept; it has numerous practical applications:
-
Scheduling: Imagine you have two events that repeat on different cycles. One event happens every 3 days, and another every 5 days. The LCM helps determine when both events will coincide again (in this case, every 15 days).
-
Fraction Addition/Subtraction: To add or subtract fractions with different denominators, you need to find the LCM of the denominators to get a common denominator.
-
Music: In music theory, LCM is used to find the least common denominator for rhythmic patterns.
-
Construction and Engineering: In construction and engineering projects, the LCM can help coordinate tasks that require different cycles or time intervals.
Frequently Asked Questions (FAQ)
-
Q: What is the difference between LCM and GCD?
- A: The LCM is the smallest common multiple, while the GCD is the greatest common divisor. They are related, but represent opposite ends of the divisibility spectrum.
-
Q: Can the LCM be larger than the largest number in the set?
- A: Yes, absolutely. This is often the case when the numbers have no common factors other than 1. For example, the LCM of 7 and 11 is 77.
-
Q: How do I find the LCM of more than three numbers?
- A: You can extend the prime factorization method or the iterative GCD method to handle any number of integers. Find the prime factorization of each number, take the highest power of each prime factor, and multiply them together. Alternatively, find the LCM of two numbers, then find the LCM of that result and the next number, and so on.
-
Q: Is there a formula to directly calculate the LCM of any number of integers?
- A: While there isn't a single, neat formula for directly calculating the LCM of any number of integers like there is for two integers using the GCD, the prime factorization method provides a systematic approach.
Conclusion
Finding the LCM, even for seemingly simple numbers like 3, 5, and 10, provides a valuable opportunity to grasp fundamental mathematical concepts. We've explored three different methods—listing multiples, prime factorization, and the GCD method—demonstrating the flexibility and depth of this important mathematical tool. Understanding LCM is not just about memorizing a process; it's about understanding the underlying principles of divisibility and number theory, skills that are highly transferable and applicable across various fields. Remember to practice these methods with different sets of numbers to build your confidence and solidify your understanding of the Least Common Multiple.
Latest Posts
Latest Posts
-
Number Of Protons In Beryllium
Sep 25, 2025
-
Why Was The Sky Yellow
Sep 25, 2025
-
Control Variable Independent And Dependent
Sep 25, 2025
-
Life Cycle Of A Flowering
Sep 25, 2025
-
Beach Nourishment Advantages And Disadvantages
Sep 25, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 3 5 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.