Lcm Of 22 And 14
dulhadulhi
Sep 22, 2025 · 6 min read
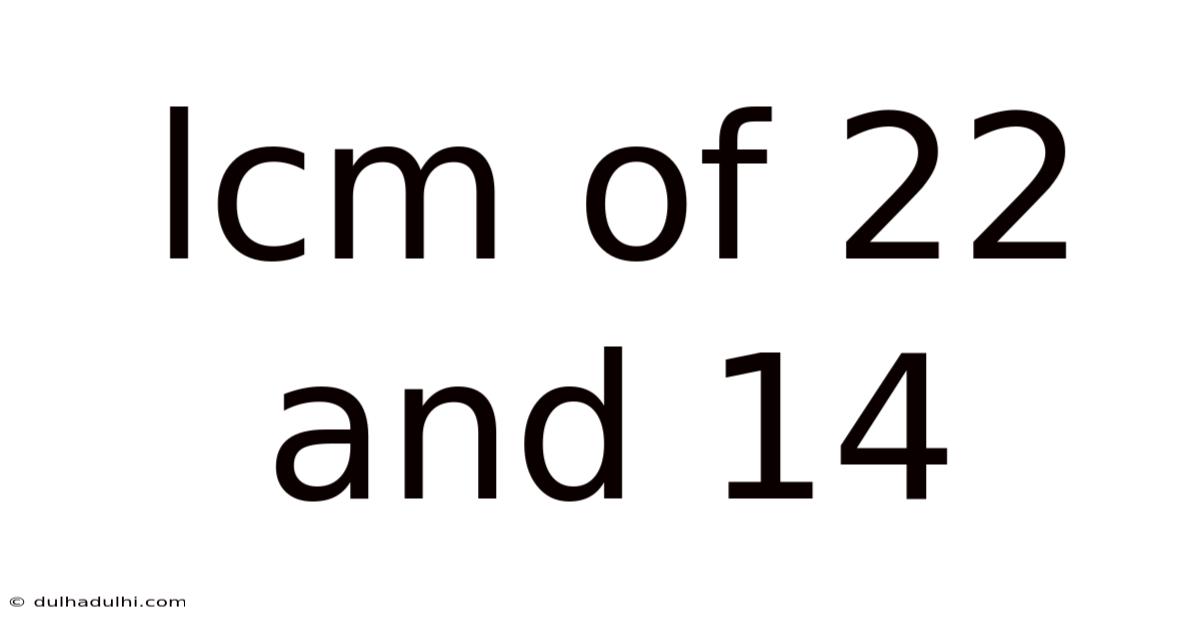
Table of Contents
Finding the Least Common Multiple (LCM) of 22 and 14: A Comprehensive Guide
Finding the least common multiple (LCM) might seem like a simple arithmetic task, but understanding the underlying concepts and different methods can be incredibly valuable, especially when dealing with larger numbers or more complex problems. This article will delve into the calculation of the LCM of 22 and 14, exploring various approaches and providing a solid foundation for understanding this fundamental concept in mathematics. We'll cover prime factorization, the greatest common divisor (GCD) method, and the listing method, ensuring you grasp the LCM concept fully.
Introduction to Least Common Multiple (LCM)
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers. In simpler terms, it's the smallest number that contains all the numbers you're considering as factors. Understanding the LCM is crucial in various mathematical applications, including solving problems related to fractions, simplifying expressions, and even scheduling tasks. For example, if you need to find when two events will happen simultaneously, again, the LCM comes into play.
Method 1: Prime Factorization
This is often considered the most fundamental method for finding the LCM. It involves breaking down each number into its prime factors – the smallest prime numbers that multiply together to give the original number. Let's apply this to 22 and 14:
Step 1: Find the prime factorization of 22.
22 = 2 x 11
Both 2 and 11 are prime numbers.
Step 2: Find the prime factorization of 14.
14 = 2 x 7
Both 2 and 7 are prime numbers.
Step 3: Identify the highest power of each prime factor present in either factorization.
In our case, the prime factors are 2, 7, and 11. The highest power of 2 is 2¹ (appearing in both factorizations), the highest power of 7 is 7¹ (from the factorization of 14), and the highest power of 11 is 11¹ (from the factorization of 22).
Step 4: Multiply the highest powers together.
LCM(22, 14) = 2¹ x 7¹ x 11¹ = 2 x 7 x 11 = 154
Therefore, the least common multiple of 22 and 14 is 154. This means 154 is the smallest positive integer that is divisible by both 22 and 14.
Method 2: Greatest Common Divisor (GCD) Method
This method leverages the relationship between the LCM and the greatest common divisor (GCD). The GCD is the largest number that divides both integers without leaving a remainder. There's a useful formula that connects the LCM and GCD:
LCM(a, b) = (|a x b|) / GCD(a, b)
Where:
- a and b are the two integers.
- |a x b| represents the absolute value of the product of a and b.
Step 1: Find the GCD of 22 and 14 using the Euclidean algorithm.
The Euclidean algorithm is an efficient method for finding the GCD. It involves repeatedly applying the division algorithm until the remainder is 0. The last non-zero remainder is the GCD.
- Divide the larger number (22) by the smaller number (14): 22 = 14 x 1 + 8
- Replace the larger number with the smaller number (14) and the smaller number with the remainder (8): 14 = 8 x 1 + 6
- Repeat: 8 = 6 x 1 + 2
- Repeat: 6 = 2 x 3 + 0
The last non-zero remainder is 2, so the GCD(22, 14) = 2.
Step 2: Apply the LCM formula.
LCM(22, 14) = (|22 x 14|) / GCD(22, 14) = (308) / 2 = 154
Again, the LCM of 22 and 14 is 154. This method provides an alternative approach and highlights the interconnectedness of LCM and GCD.
Method 3: Listing Multiples Method
This is a more straightforward, albeit less efficient method, especially for larger numbers. It involves listing the multiples of each number until a common multiple is found.
Step 1: List the multiples of 22.
22, 44, 66, 88, 110, 132, 154, 176, ...
Step 2: List the multiples of 14.
14, 28, 42, 56, 70, 84, 98, 112, 126, 140, 154, 168,...
Step 3: Identify the smallest common multiple.
The smallest multiple that appears in both lists is 154.
Therefore, the LCM(22, 14) = 154. While this method is simple to understand, it becomes less practical with larger numbers as the list of multiples can grow quite long.
Understanding the Significance of LCM
The LCM has practical applications beyond simple arithmetic exercises. Here are a few examples:
-
Fraction addition and subtraction: To add or subtract fractions with different denominators, you need to find the LCM of the denominators to create a common denominator.
-
Scheduling: Imagine two buses arrive at a stop every 22 minutes and 14 minutes respectively. The LCM (154 minutes) tells you when both buses will arrive at the stop simultaneously.
-
Cyclic patterns: LCM helps analyze repeating patterns or cycles that occur at different intervals. This is useful in various fields, including physics and engineering.
-
Modular arithmetic: LCM plays a role in modular arithmetic which has applications in cryptography and computer science.
Frequently Asked Questions (FAQ)
-
What is the difference between LCM and GCD? The LCM is the smallest common multiple, while the GCD is the largest common divisor. They are related through the formula: LCM(a,b) = (|a*b|) / GCD(a,b).
-
Can the LCM of two numbers be one of the numbers? Yes, if one number is a multiple of the other, the LCM will be the larger number. For example, LCM(2,4) = 4.
-
Is there a formula for finding the LCM of more than two numbers? Yes, you can extend the prime factorization method to find the LCM of any number of integers. Find the prime factorization of each number, then take the highest power of each prime factor present and multiply them together. The GCD method can also be extended using more advanced techniques.
-
Why is the prime factorization method considered the most fundamental? It directly reveals the building blocks (prime factors) of the numbers involved, offering a clear and intuitive understanding of why the LCM is what it is.
-
What if the numbers are negative? The absolute value of the numbers is used when calculating LCM. The LCM is always a positive integer.
Conclusion
Finding the LCM of 22 and 14, as demonstrated through different methods, provides a solid foundation for understanding this fundamental concept. Whether you utilize prime factorization, the GCD method, or the listing multiples method, the result remains consistent: the LCM of 22 and 14 is 154. Mastering LCM calculation not only strengthens your arithmetic skills but also provides a valuable tool for tackling more complex mathematical problems across various disciplines. Remember, the choice of method depends on the context and the complexity of the numbers involved. Understanding the underlying principles will empower you to efficiently solve LCM problems in any situation. From simple fraction operations to complex scheduling scenarios, the LCM is a crucial concept with wide-ranging applications.
Latest Posts
Latest Posts
-
What Is 40 Of 100
Sep 22, 2025
-
Perimeter Of Sector In Radians
Sep 22, 2025
-
Factors That Affect Enzyme Function
Sep 22, 2025
-
Adaptations Of The Small Intestine
Sep 22, 2025
-
What Alcohol Content Is Beer
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 22 And 14 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.