Lcm Of 21 And 77
dulhadulhi
Sep 24, 2025 · 6 min read
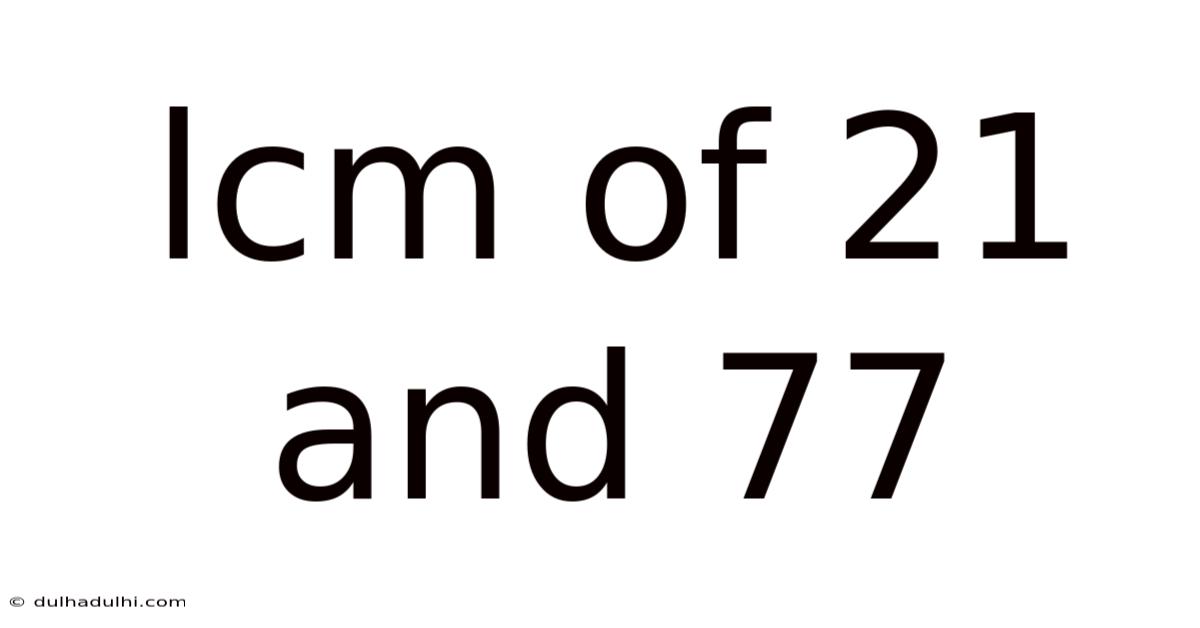
Table of Contents
Finding the LCM of 21 and 77: A Deep Dive into Least Common Multiples
Finding the least common multiple (LCM) of two numbers is a fundamental concept in mathematics, crucial for various applications from simplifying fractions to solving complex algebraic problems. This article will guide you through the process of calculating the LCM of 21 and 77, exploring different methods and providing a deeper understanding of the underlying principles. We'll also delve into the concept of LCM itself, exploring its significance and practical applications beyond simple arithmetic. By the end, you'll not only know the LCM of 21 and 77 but also possess a robust understanding of how to find the LCM of any two numbers.
Understanding Least Common Multiples (LCM)
Before we dive into calculating the LCM of 21 and 77, let's establish a clear understanding of what a least common multiple actually is. The LCM of two or more integers is the smallest positive integer that is divisible by all the integers. In simpler terms, it's the smallest number that contains all the given numbers as factors. For example, the LCM of 2 and 3 is 6 because 6 is the smallest number divisible by both 2 and 3.
Method 1: Listing Multiples
One straightforward method to find the LCM is by listing the multiples of each number until a common multiple is found. Let's apply this to 21 and 77:
- Multiples of 21: 21, 42, 63, 84, 105, 126, 147, 168, 189, 210, 231, ...
- Multiples of 77: 77, 154, 231, ...
By comparing the lists, we can see that the smallest common multiple is 231. Therefore, the LCM of 21 and 77 is 231. While this method is simple for smaller numbers, it can become cumbersome and time-consuming for larger numbers.
Method 2: Prime Factorization
A more efficient method, especially for larger numbers, involves using prime factorization. Prime factorization is the process of breaking down a number into its prime factors – numbers that are only divisible by 1 and themselves.
Let's find the prime factorization of 21 and 77:
- 21: 3 x 7
- 77: 7 x 11
Now, to find the LCM, we take the highest power of each prime factor present in the factorizations:
- The prime factors are 3, 7, and 11.
- The highest power of 3 is 3¹ = 3
- The highest power of 7 is 7¹ = 7
- The highest power of 11 is 11¹ = 11
Multiplying these highest powers together gives us the LCM: 3 x 7 x 11 = 231. This method is significantly more efficient than listing multiples, particularly when dealing with larger numbers.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and the greatest common divisor (GCD) are closely related. The GCD is the largest number that divides both given numbers without leaving a remainder. There's a formula that elegantly links the LCM and GCD:
LCM(a, b) x GCD(a, b) = a x b
Where 'a' and 'b' are the two numbers.
Let's first find the GCD of 21 and 77 using the Euclidean algorithm:
- Divide 77 by 21: 77 = 21 x 3 + 14
- Divide 21 by the remainder 14: 21 = 14 x 1 + 7
- Divide 14 by the remainder 7: 14 = 7 x 2 + 0
The last non-zero remainder is 7, so the GCD(21, 77) = 7.
Now, using the formula:
LCM(21, 77) = (21 x 77) / GCD(21, 77) = (21 x 77) / 7 = 231
This method offers another efficient way to calculate the LCM, particularly useful when working with larger numbers where prime factorization might become more complex.
A Deeper Look at Prime Factorization and its Role in LCM Calculation
The prime factorization method offers a powerful and insightful approach to understanding LCMs. By breaking down the numbers into their prime factors, we reveal the fundamental building blocks of the numbers. The LCM then becomes a combination of these building blocks, ensuring that it contains all the factors of both original numbers. This highlights the fundamental theorem of arithmetic, which states that every integer greater than 1 can be represented uniquely as a product of prime numbers (ignoring the order of the factors).
This method’s efficiency stems from the fact that it avoids unnecessary calculations. Listing multiples might involve exploring many multiples before finding a common one. In contrast, prime factorization directly targets the essential components of the numbers, leading to a more direct calculation of the LCM.
Applications of LCM in Real-World Scenarios
The concept of LCM extends far beyond simple mathematical exercises. It has practical applications in numerous fields:
-
Scheduling: Imagine two buses arrive at a bus stop at different intervals. The LCM helps determine when both buses will arrive at the stop simultaneously. For instance, if one bus arrives every 21 minutes and another every 77 minutes, the LCM (231 minutes) represents the time until they arrive together again.
-
Fraction Operations: Finding the LCM of denominators is crucial when adding or subtracting fractions. It allows you to find a common denominator, making the calculation straightforward.
-
Cyclic Events: In scenarios involving recurring events, the LCM can help determine when the events coincide. Think about planetary alignments or repeating patterns in nature.
-
Engineering and Construction: The LCM finds application in problems related to timing and synchronization of various components in a system.
-
Music Theory: LCM plays a role in understanding musical intervals and harmonies.
Frequently Asked Questions (FAQ)
Q: Is there only one LCM for two numbers?
A: Yes, there is only one least common multiple for any two numbers. There are many common multiples, but only one is the smallest.
Q: What if one of the numbers is 0?
A: The LCM of any number and 0 is undefined because 0 has infinitely many multiples.
Q: Can I use a calculator to find the LCM?
A: Many scientific calculators and online calculators have built-in functions to calculate the LCM of two or more numbers.
Q: What if the numbers have more than one common factor?
A: The prime factorization method elegantly handles this. The highest power of each prime factor, regardless of how many times it appears in the factorization of each number, is included in the LCM calculation.
Conclusion
Finding the LCM of 21 and 77, as demonstrated through multiple methods, is a simple yet fundamental concept with widespread applications. Understanding the different approaches – listing multiples, prime factorization, and using the GCD – equips you with versatile tools for tackling various LCM problems. The key is to choose the method that best suits the numbers involved and your comfort level with mathematical techniques. The prime factorization method, however, offers a superior efficiency, especially as numbers become larger and more complex. Remember, mastering the LCM not only enhances your mathematical skills but also opens doors to solving real-world problems across diverse disciplines. So, whether you're dealing with bus schedules, fraction simplification, or more complex applications, the concept of the least common multiple remains a valuable asset in your mathematical toolkit.
Latest Posts
Latest Posts
-
Practice On Balancing Chemical Equations
Sep 24, 2025
-
Angle Between Line And Plane
Sep 24, 2025
-
How Big Is Two Inches
Sep 24, 2025
-
Factors Of 72 In Pairs
Sep 24, 2025
-
Do Gold Stick To Magnets
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 21 And 77 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.