Lcm Of 15 And 9
dulhadulhi
Sep 24, 2025 · 7 min read
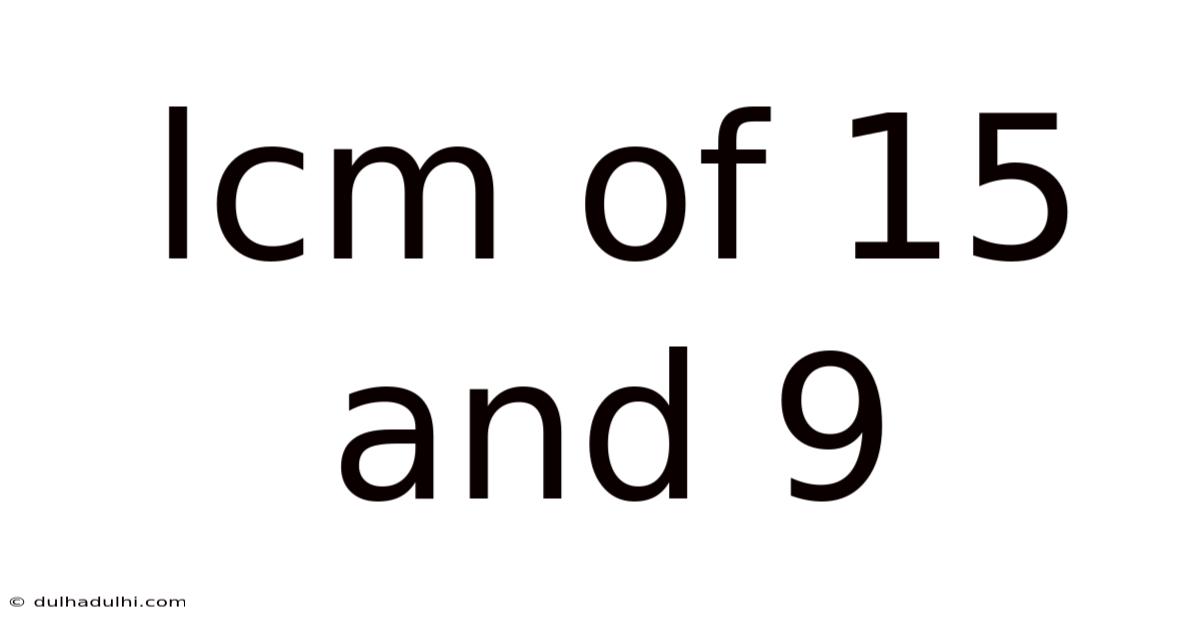
Table of Contents
Finding the LCM of 15 and 9: A Comprehensive Guide
Finding the least common multiple (LCM) of two numbers might seem like a simple arithmetic task, but understanding the underlying concepts is crucial for grasping more advanced mathematical ideas. This article provides a comprehensive guide on how to find the LCM of 15 and 9, exploring different methods and delving into the theoretical underpinnings. We'll not only show you how to find the LCM but also why these methods work, making this a valuable resource for students and anyone looking to refresh their understanding of number theory.
Introduction: What is the Least Common Multiple (LCM)?
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers. Think of it as the smallest number that contains all the numbers you're working with as factors. For instance, if we're looking at the numbers 2 and 3, their LCM is 6 because 6 is the smallest number that is divisible by both 2 and 3. Understanding the LCM is essential in various areas of mathematics, including fractions, solving equations, and tackling more complex problems in algebra and number theory.
Methods for Finding the LCM of 15 and 9
There are several efficient methods to determine the LCM of two numbers, particularly useful numbers like 15 and 9. Let's explore the most common approaches:
1. Listing Multiples Method:
This method is straightforward, especially for smaller numbers. We list the multiples of each number until we find the smallest multiple that is common to both.
- Multiples of 15: 15, 30, 45, 60, 75, 90, 105...
- Multiples of 9: 9, 18, 27, 36, 45, 54, 63, 72, 81, 90, 99...
Notice that the smallest number appearing in both lists is 45. Therefore, the LCM of 15 and 9 is 45. While simple, this method can become cumbersome with larger numbers.
2. Prime Factorization Method:
This is a more powerful and efficient method, especially when dealing with larger numbers or multiple numbers. It leverages the fundamental theorem of arithmetic, which states that every integer greater than 1 can be uniquely represented as a product of prime numbers.
- Prime factorization of 15: 3 x 5
- Prime factorization of 9: 3 x 3 = 3²
To find the LCM using prime factorization:
- Identify the prime factors: We have 3 and 5.
- Find the highest power of each prime factor: The highest power of 3 is 3² (from the factorization of 9), and the highest power of 5 is 5¹ (from the factorization of 15).
- Multiply the highest powers: 3² x 5 = 9 x 5 = 45
Therefore, the LCM of 15 and 9 is 45. This method is generally preferred for its efficiency and applicability to larger numbers.
3. Greatest Common Divisor (GCD) Method:
This method uses the relationship between the LCM and the greatest common divisor (GCD) of two numbers. The GCD is the largest number that divides both numbers without leaving a remainder. There's a crucial formula connecting the LCM and GCD:
LCM(a, b) x GCD(a, b) = a x b
where 'a' and 'b' are the two numbers.
Let's find the GCD of 15 and 9 using the Euclidean algorithm:
- Divide the larger number (15) by the smaller number (9): 15 ÷ 9 = 1 with a remainder of 6.
- Replace the larger number with the smaller number (9) and the smaller number with the remainder (6): 9 ÷ 6 = 1 with a remainder of 3.
- Repeat: 6 ÷ 3 = 2 with a remainder of 0.
- The last non-zero remainder is the GCD. In this case, the GCD(15, 9) = 3.
Now, using the formula:
LCM(15, 9) x GCD(15, 9) = 15 x 9 LCM(15, 9) x 3 = 135 LCM(15, 9) = 135 ÷ 3 = 45
This method elegantly demonstrates the connection between the LCM and GCD, providing another way to solve the problem.
Explanation of the Concepts: A Deeper Dive
Let's delve deeper into the underlying mathematical principles behind the LCM.
-
Divisibility: A number 'a' is divisible by a number 'b' if the remainder is 0 when 'a' is divided by 'b'. This means 'b' is a factor of 'a'.
-
Multiples: A multiple of a number is the product of that number and any integer. For example, the multiples of 3 are 3, 6, 9, 12, 15, and so on.
-
Prime Numbers: A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. Prime numbers are the building blocks of all other numbers.
-
Prime Factorization: Expressing a number as a product of its prime factors is called prime factorization. This is a unique representation for every integer greater than 1. For example, the prime factorization of 12 is 2² x 3.
-
Fundamental Theorem of Arithmetic: This theorem ensures that the prime factorization of any integer greater than 1 is unique (except for the order of the factors). This uniqueness is what allows the prime factorization method to reliably find the LCM.
-
The Relationship between LCM and GCD: The formula LCM(a, b) x GCD(a, b) = a x b highlights the intricate relationship between the LCM and GCD. This relationship is a fundamental concept in number theory. It provides an alternative, and often more efficient, method to calculate the LCM. The Euclidean algorithm, used to find the GCD, is an efficient algorithm that minimizes the number of computations needed.
Applications of LCM in Real-World Scenarios
The LCM isn't just a theoretical concept; it has practical applications in various fields:
-
Scheduling: Imagine two buses arrive at a bus stop at different intervals. The LCM helps determine when both buses will arrive at the stop simultaneously.
-
Fraction Arithmetic: When adding or subtracting fractions, finding the LCM of the denominators is crucial for finding a common denominator.
-
Construction and Engineering: In construction projects or engineering designs involving repetitive patterns or cycles, the LCM helps in planning and coordination.
-
Music: In musical compositions, rhythmic patterns often rely on finding common multiples to create harmonious sequences.
Frequently Asked Questions (FAQ)
-
Q: What if I have more than two numbers?
- A: You can extend the prime factorization method or the GCD method to find the LCM of more than two numbers. For the prime factorization method, you consider all prime factors and their highest powers across all the numbers. For the GCD method, you can find the LCM iteratively, starting with two numbers and then finding the LCM of that result with the next number, and so on.
-
Q: Is there a formula to directly calculate the LCM of any two numbers?
- A: While there's no single formula that directly calculates the LCM without involving prime factorization or the GCD, the formula LCM(a, b) * GCD(a, b) = a * b provides a powerful indirect method.
-
Q: What if the numbers are very large?
- A: For very large numbers, specialized algorithms are used to efficiently find the GCD and subsequently the LCM. These algorithms are often implemented in computer programs.
-
Q: Why is the prime factorization method considered more efficient?
- A: The prime factorization method is generally more efficient because it systematically breaks down the numbers into their fundamental building blocks, directly identifying the elements necessary to construct the LCM. The listing method can become impractical for large numbers, while the GCD method requires an additional calculation (finding the GCD) before arriving at the LCM.
Conclusion: Mastering the LCM
Finding the least common multiple of 15 and 9, as we've demonstrated, can be achieved through several methods. While the listing multiples method is intuitive for smaller numbers, the prime factorization and GCD methods offer greater efficiency and scalability for larger numbers and more complex problems. Understanding these methods and the underlying principles of divisibility, prime factorization, and the relationship between LCM and GCD equips you with a powerful toolset for tackling various mathematical challenges. This knowledge extends beyond simple arithmetic, proving vital in various fields and furthering your understanding of fundamental mathematical concepts. Remember, the key is not just to find the answer (45 in this case) but to understand why that answer is correct, which is the foundation for mastering more advanced mathematical concepts.
Latest Posts
Latest Posts
-
7 25 As A Decimal
Sep 24, 2025
-
Stress And Urinary Tract Infections
Sep 24, 2025
-
What Is Brass Composed Of
Sep 24, 2025
-
What Are The Common Multiples
Sep 24, 2025
-
Are Polar Bears From Antarctica
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 15 And 9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.