Lcm Of 12 And 30
dulhadulhi
Sep 23, 2025 · 5 min read
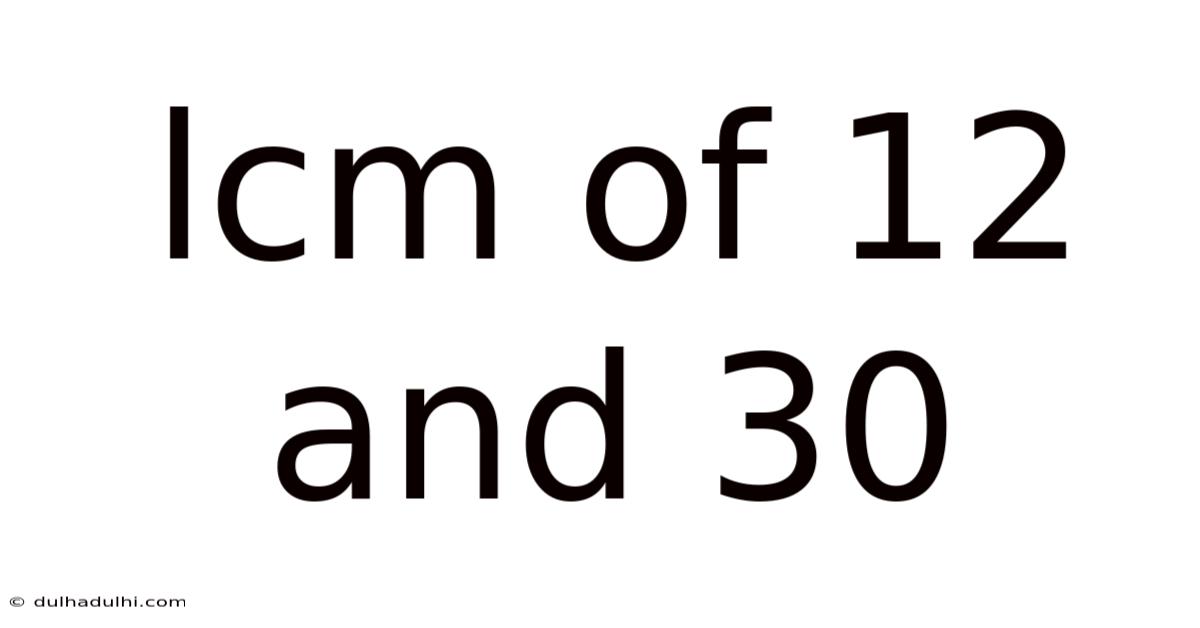
Table of Contents
Finding the Least Common Multiple (LCM) of 12 and 30: A Comprehensive Guide
Finding the least common multiple (LCM) might seem like a simple arithmetic task, but understanding the underlying concepts and different methods for calculating it is crucial for a strong foundation in mathematics. This article will delve deep into calculating the LCM of 12 and 30, exploring various techniques, explaining the underlying mathematical principles, and providing practical applications. Whether you're a student brushing up on your math skills or simply curious about the concept, this guide will provide you with a comprehensive understanding of LCM and its applications. We'll cover everything from the definition of LCM to advanced methods and real-world examples.
Understanding the Least Common Multiple (LCM)
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers. In simpler terms, it's the smallest number that all the given numbers can divide into evenly without leaving a remainder. Understanding the LCM is essential for solving various mathematical problems, including simplifying fractions, finding common denominators, and solving problems involving ratios and proportions.
Let's consider our example: finding the LCM of 12 and 30. This means we need to find the smallest positive integer that is divisible by both 12 and 30.
Method 1: Listing Multiples
One of the simplest methods to find the LCM is by listing the multiples of each number until you find the smallest common multiple.
Multiples of 12: 12, 24, 36, 48, 60, 72, 84, 96, 108, 120, ...
Multiples of 30: 30, 60, 90, 120, 150, ...
By comparing the lists, we can see that the smallest number that appears in both lists is 60. Therefore, the LCM of 12 and 30 is 60. This method is straightforward but can become cumbersome when dealing with larger numbers.
Method 2: Prime Factorization
This method is more efficient, especially when dealing with larger numbers. It involves breaking down each number into its prime factors. Prime factorization is the process of expressing a number as a product of its prime numbers (numbers only divisible by 1 and themselves).
- Prime factorization of 12: 2 x 2 x 3 = 2² x 3
- Prime factorization of 30: 2 x 3 x 5
Now, we identify the highest power of each prime factor present in either factorization:
- The highest power of 2 is 2² = 4
- The highest power of 3 is 3¹ = 3
- The highest power of 5 is 5¹ = 5
To find the LCM, we multiply these highest powers together:
LCM(12, 30) = 2² x 3 x 5 = 4 x 3 x 5 = 60
This method provides a more systematic and efficient approach, especially beneficial when dealing with larger numbers or multiple numbers.
Method 3: Greatest Common Divisor (GCD) Method
The LCM and the greatest common divisor (GCD) of two numbers are related. The GCD is the largest number that divides both numbers without leaving a remainder. We can use the following formula to find the LCM using the GCD:
LCM(a, b) = (|a x b|) / GCD(a, b)
First, let's find the GCD of 12 and 30. We can use the Euclidean algorithm for this:
- Divide the larger number (30) by the smaller number (12): 30 ÷ 12 = 2 with a remainder of 6.
- Replace the larger number with the smaller number (12) and the smaller number with the remainder (6): 12 ÷ 6 = 2 with a remainder of 0.
- Since the remainder is 0, the GCD is the last non-zero remainder, which is 6.
Now, we can use the formula:
LCM(12, 30) = (12 x 30) / 6 = 360 / 6 = 60
This method elegantly connects the concepts of LCM and GCD, providing another efficient way to calculate the LCM.
Illustrative Examples and Applications
The concept of LCM has numerous real-world applications:
-
Scheduling: Imagine two buses arrive at a bus stop at different intervals. One bus arrives every 12 minutes, and the other every 30 minutes. To find out when both buses will arrive at the same time, you need to find the LCM of 12 and 30, which is 60. Both buses will arrive together every 60 minutes (or 1 hour).
-
Fraction Operations: When adding or subtracting fractions with different denominators, you need to find the LCM of the denominators to find a common denominator. For example, adding 1/12 and 1/30 requires finding the LCM of 12 and 30 (which is 60), converting the fractions to have a denominator of 60, and then adding them.
-
Gear Ratios: In mechanics, gear ratios often involve finding the LCM to determine the synchronization of rotating components.
-
Tiling and Pattern Repetition: LCM is crucial in designing repeating patterns or tiling arrangements where you need to ensure the patterns align perfectly.
Frequently Asked Questions (FAQ)
Q: What if I have more than two numbers?
A: The methods described above can be extended to find the LCM of more than two numbers. For prime factorization, you simply find the highest power of each prime factor present in any of the factorizations. For the GCD method, you would iteratively find the GCD of pairs of numbers and then apply the formula accordingly.
Q: Is there a single "best" method?
A: The "best" method depends on the numbers involved and your personal preference. For small numbers, listing multiples might be sufficient. For larger numbers, prime factorization is generally more efficient. The GCD method provides a powerful connection between LCM and GCD.
Q: What is the LCM of 1 and any other number?
A: The LCM of 1 and any other number is always the other number. This is because 1 divides evenly into any number.
Conclusion
Understanding the least common multiple is fundamental to various mathematical concepts and real-world applications. We explored three distinct methods – listing multiples, prime factorization, and the GCD method – for calculating the LCM of 12 and 30, arriving at the answer 60 in each case. The choice of method depends largely on the context and the complexity of the numbers involved. Mastering these techniques will not only enhance your mathematical proficiency but also equip you with practical tools applicable in diverse fields. Remember, the key is to grasp the underlying principles and choose the method best suited to the situation. This comprehensive guide provides a solid foundation for further exploration of LCM and its significance in mathematics and beyond.
Latest Posts
Latest Posts
-
Area Of Triangle Using Vectors
Sep 23, 2025
-
What Is The Material Resin
Sep 23, 2025
-
Charge Of A Zinc Ion
Sep 23, 2025
-
7 4 As A Decimal
Sep 23, 2025
-
L C M Of 10 And 12
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 12 And 30 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.