Lcm Of 10 And 4
dulhadulhi
Sep 23, 2025 · 6 min read
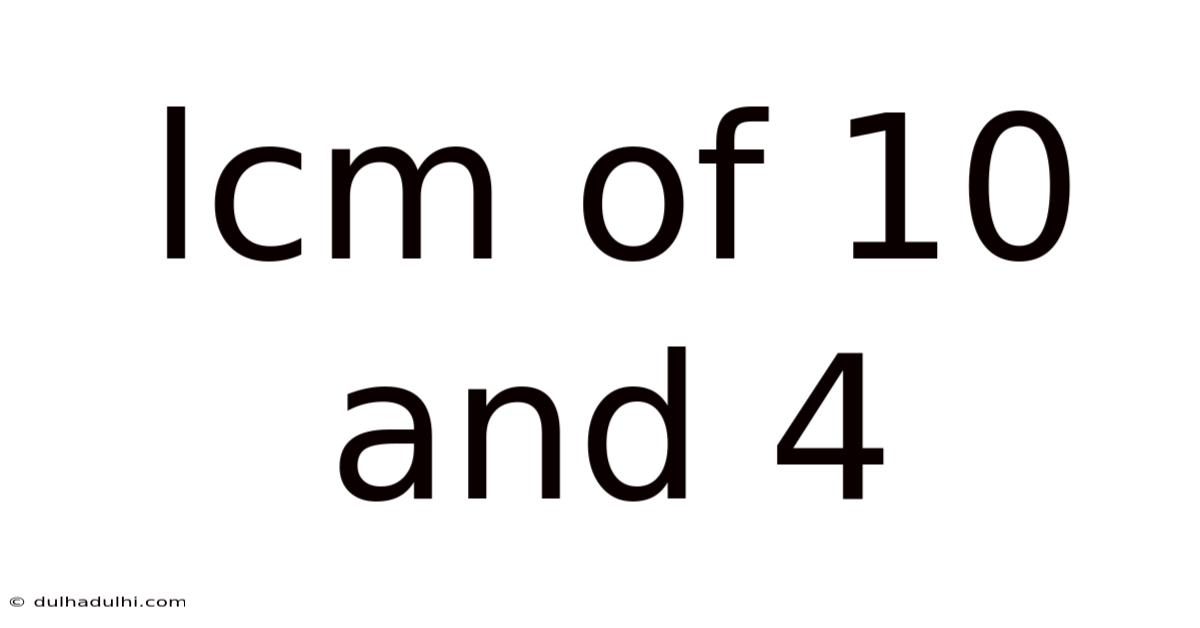
Table of Contents
Finding the LCM of 10 and 4: A Deep Dive into Least Common Multiples
Finding the least common multiple (LCM) of two numbers might seem like a simple arithmetic task, but understanding the underlying concepts reveals a fascinating journey into number theory. This article explores the LCM of 10 and 4, demonstrating several methods to calculate it and delving into the broader significance of LCMs in mathematics and real-world applications. We'll cover various approaches, ensuring a thorough understanding for learners of all levels.
Understanding Least Common Multiples (LCM)
Before we dive into calculating the LCM of 10 and 4, let's establish a firm grasp of the concept. The least common multiple (LCM) of two or more integers is the smallest positive integer that is a multiple of all the integers. In simpler terms, it's the smallest number that both (or all) numbers divide into evenly.
For example, let's consider the numbers 2 and 3. Multiples of 2 are 2, 4, 6, 8, 10, 12... and multiples of 3 are 3, 6, 9, 12, 15... The smallest number that appears in both lists is 6. Therefore, the LCM of 2 and 3 is 6.
Method 1: Listing Multiples
This is the most straightforward method, especially for smaller numbers like 10 and 4. We list the multiples of each number until we find the smallest common multiple.
- Multiples of 10: 10, 20, 30, 40, 50, 60...
- Multiples of 4: 4, 8, 12, 16, 20, 24, 28, 32, 36, 40...
Notice that 20 appears in both lists. However, we see that 20 is also present, making it the smallest common multiple. Therefore, the LCM(10, 4) = 20.
This method is simple and intuitive but can become cumbersome for larger numbers. Finding the LCM of, say, 144 and 252 by this method would require listing a substantial number of multiples.
Method 2: Prime Factorization
Prime factorization offers a more efficient and systematic approach, especially when dealing with larger numbers. This method involves breaking down each number into its prime factors – numbers divisible only by 1 and themselves.
- Prime factorization of 10: 2 x 5
- Prime factorization of 4: 2 x 2 = 2²
To find the LCM using prime factorization:
- Identify all the prime factors: In this case, we have 2 and 5.
- Take the highest power of each prime factor: The highest power of 2 is 2² (from the factorization of 4), and the highest power of 5 is 5¹ (from the factorization of 10).
- Multiply the highest powers together: 2² x 5 = 4 x 5 = 20
Therefore, the LCM(10, 4) = 20 using the prime factorization method. This method is significantly more efficient for larger numbers because it avoids the potentially lengthy process of listing multiples.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and GCD (greatest common divisor) of two numbers are closely related. The GCD is the largest number that divides both numbers evenly. There's a handy formula that connects the LCM and GCD:
LCM(a, b) x GCD(a, b) = a x b
Let's use this formula for 10 and 4:
- Find the GCD of 10 and 4: The common divisors of 10 and 4 are 1 and 2. The greatest common divisor is 2. Therefore, GCD(10, 4) = 2.
- Apply the formula: LCM(10, 4) x GCD(10, 4) = 10 x 4 LCM(10, 4) x 2 = 40 LCM(10, 4) = 40 / 2 = 20
This method elegantly connects the concepts of LCM and GCD, providing another efficient way to calculate the LCM.
Method 4: Using the Euclidean Algorithm (for GCD Calculation)
When dealing with larger numbers, finding the GCD directly can be challenging. The Euclidean Algorithm provides a systematic method for finding the GCD. Let's illustrate this with 10 and 4:
- Divide the larger number (10) by the smaller number (4): 10 ÷ 4 = 2 with a remainder of 2.
- Replace the larger number with the smaller number (4) and the smaller number with the remainder (2): Now we have 4 and 2.
- Repeat the process: 4 ÷ 2 = 2 with a remainder of 0.
- The GCD is the last non-zero remainder: In this case, the GCD is 2.
Once you have the GCD (2), you can use the formula from Method 3 to calculate the LCM:
LCM(10, 4) = (10 x 4) / GCD(10, 4) = 40 / 2 = 20
Real-World Applications of LCM
Understanding LCMs extends far beyond abstract mathematical concepts. They find practical applications in various fields:
-
Scheduling: Imagine two buses arrive at a bus stop at different intervals. One bus arrives every 10 minutes, and another arrives every 4 minutes. The LCM (20 minutes) determines when both buses will arrive simultaneously at the bus stop.
-
Project Management: Consider a project with two tasks. One takes 10 hours, and the other takes 4 hours. Knowing the LCM (20 hours) helps determine the minimum time needed to complete both tasks.
-
Music: LCMs are crucial in music theory for determining the least common multiple of the lengths of different musical phrases or rhythms, helping in harmonizing and creating musical patterns.
-
Construction: In construction projects, the LCM can help coordinate the timing of different tasks with varying durations.
-
Manufacturing: In manufacturing processes involving machines that operate at different speeds, the LCM helps optimize production schedules and coordination of multiple machines.
Frequently Asked Questions (FAQ)
Q1: What if the two numbers are the same?
If the two numbers are identical (e.g., LCM of 10 and 10), then the LCM is simply the number itself. LCM(10, 10) = 10
Q2: What is the LCM of more than two numbers?
To find the LCM of more than two numbers, you can extend the prime factorization method. Find the prime factorization of each number, take the highest power of each prime factor present in any of the factorizations, and multiply them together.
Q3: Can the LCM be larger than the product of the two numbers?
No, the LCM of two numbers will always be less than or equal to the product of the two numbers.
Q4: Is there a formula for finding the LCM of three or more numbers?
There isn't a single, concise formula like the one for two numbers. However, the prime factorization method effectively handles any number of inputs.
Conclusion
Calculating the LCM of 10 and 4, while seemingly straightforward, provides a valuable stepping stone to understanding broader concepts within number theory. We've explored several methods – listing multiples, prime factorization, and utilizing the GCD – each offering unique advantages depending on the numbers involved. Understanding LCMs isn't just about solving mathematical problems; it's about developing a deeper appreciation for the underlying mathematical principles and their relevance to diverse real-world scenarios. Mastering these methods will empower you to tackle more complex problems and appreciate the elegant interconnectedness of mathematical concepts. Remember, the key is to choose the method that best suits your needs and the complexity of the numbers involved. Whether you prefer the simplicity of listing multiples for smaller numbers or the efficiency of prime factorization for larger ones, a strong grasp of these concepts will serve you well in various mathematical endeavors.
Latest Posts
Latest Posts
-
Subtract Fraction With Different Denominators
Sep 23, 2025
-
Half A Yard In Cm
Sep 23, 2025
-
Energy In A Light Bulb
Sep 23, 2025
-
Test For Aldehydes And Ketones
Sep 23, 2025
-
What Is 5 Of 150000
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 10 And 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.