Lcm For 4 And 7
dulhadulhi
Sep 24, 2025 · 6 min read
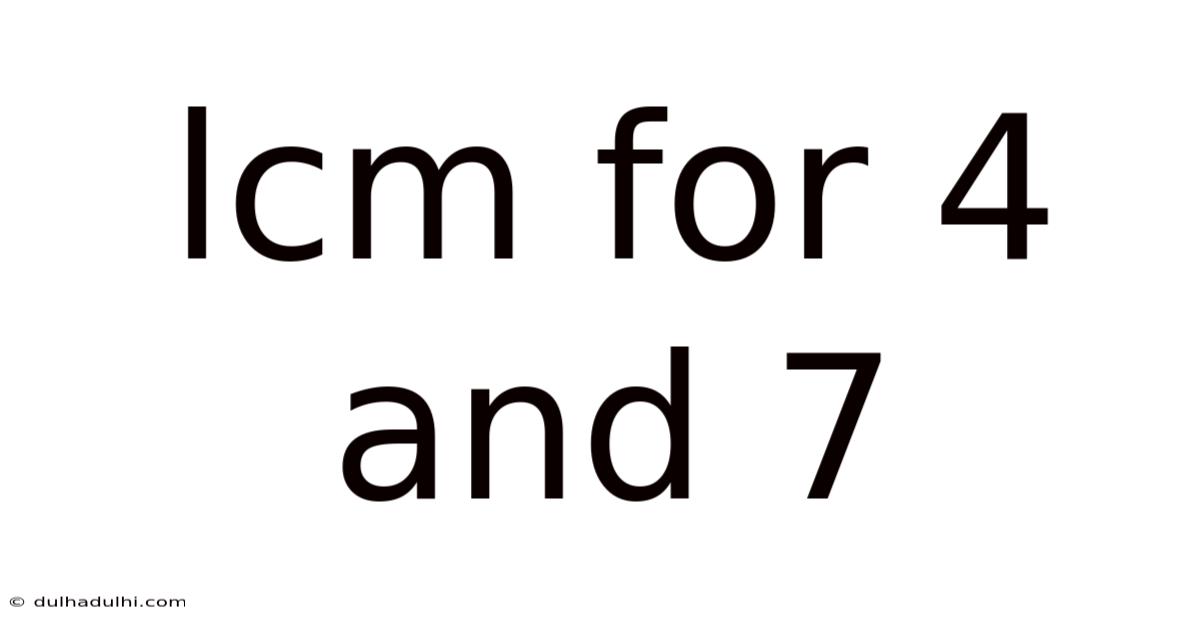
Table of Contents
Finding the Least Common Multiple (LCM) of 4 and 7: A Comprehensive Guide
Finding the least common multiple (LCM) is a fundamental concept in mathematics, crucial for various applications from simplifying fractions to solving complex problems in algebra and beyond. This comprehensive guide will walk you through understanding and calculating the LCM of 4 and 7, exploring different methods and delving into the underlying mathematical principles. We'll cover everything from basic definitions to advanced techniques, ensuring you grasp the concept thoroughly.
Understanding Least Common Multiple (LCM)
Before we dive into finding the LCM of 4 and 7, let's clarify what the LCM actually represents. The least common multiple of two or more integers is the smallest positive integer that is a multiple of all the integers. In simpler terms, it's the smallest number that both (or all) of your starting numbers can divide into evenly. This concept is distinct from the greatest common divisor (GCD), which is the largest number that divides both numbers without leaving a remainder.
For example, consider the numbers 6 and 8. The multiples of 6 are 6, 12, 18, 24, 30, and so on. The multiples of 8 are 8, 16, 24, 32, and so on. The smallest number that appears in both lists is 24; therefore, the LCM of 6 and 8 is 24.
Method 1: Listing Multiples
This is the most straightforward method, especially for smaller numbers like 4 and 7. We'll list the multiples of each number until we find the smallest common multiple.
- Multiples of 4: 4, 8, 12, 16, 20, 24, 28, 32, 36, 40...
- Multiples of 7: 7, 14, 21, 28, 35, 42, 49...
By comparing the lists, we can see that the smallest number that appears in both lists is 28. Therefore, the LCM of 4 and 7 is 28.
This method works well for small numbers, but it becomes less efficient as the numbers get larger. Imagine trying to find the LCM of 126 and 252 using this method! You'd need to list a considerable number of multiples before you find the common one.
Method 2: Prime Factorization
Prime factorization is a more powerful and efficient method for finding the LCM, especially for larger numbers. This method involves breaking down each number into its prime factors. A prime factor is a number that is only divisible by 1 and itself (e.g., 2, 3, 5, 7, 11, etc.).
Let's find the prime factorization of 4 and 7:
- 4: 2 x 2 = 2²
- 7: 7 (7 is a prime number)
Now, to find the LCM using prime factorization, we follow these steps:
- Identify the prime factors: We have 2 and 7.
- Find the highest power of each prime factor: The highest power of 2 is 2² (from the factorization of 4), and the highest power of 7 is 7¹ (from the factorization of 7).
- Multiply the highest powers together: 2² x 7¹ = 4 x 7 = 28
Therefore, the LCM of 4 and 7, using prime factorization, is 28. This method is far more efficient than listing multiples, especially when dealing with larger numbers that have many factors.
Method 3: Using the Formula (LCM and GCD Relationship)
There's a fundamental relationship between the LCM and the greatest common divisor (GCD) of two numbers. The formula is:
LCM(a, b) x GCD(a, b) = a x b
Where 'a' and 'b' are the two numbers.
First, let's find the GCD of 4 and 7 using the Euclidean algorithm:
- Divide the larger number (7) by the smaller number (4): 7 ÷ 4 = 1 with a remainder of 3.
- Replace the larger number with the smaller number (4) and the smaller number with the remainder (3): 4 ÷ 3 = 1 with a remainder of 1.
- Repeat the process: 3 ÷ 1 = 3 with a remainder of 0.
- The last non-zero remainder is the GCD. In this case, the GCD(4, 7) = 1.
Now, we can use the formula:
LCM(4, 7) x GCD(4, 7) = 4 x 7 LCM(4, 7) x 1 = 28 LCM(4, 7) = 28
This method provides another way to arrive at the LCM, highlighting the interconnectedness of LCM and GCD.
Why is the LCM Important?
Understanding and calculating the LCM is vital for several mathematical operations and real-world applications:
- Simplifying Fractions: When adding or subtracting fractions with different denominators, you need to find the LCM of the denominators to create a common denominator.
- Solving Problems Involving Cycles: Consider scenarios where events repeat at different intervals (e.g., two buses arriving at a stop every 4 minutes and 7 minutes, respectively). The LCM helps determine when both buses will arrive simultaneously.
- Understanding Rhythms and Patterns: In music and other fields involving rhythmic patterns, the LCM helps determine when patterns will align.
- Algebra and Number Theory: The LCM plays a crucial role in various algebraic manipulations and number-theoretic proofs.
LCM for Larger Numbers: A Worked Example
Let's extend our understanding by calculating the LCM of two larger numbers: 18 and 24.
Method 1 (Listing Multiples): This becomes tedious for larger numbers.
Method 2 (Prime Factorization):
- 18: 2 x 3 x 3 = 2¹ x 3²
- 24: 2 x 2 x 2 x 3 = 2³ x 3¹
- Highest power of 2: 2³
- Highest power of 3: 3²
- LCM = 2³ x 3² = 8 x 9 = 72
Method 3 (Using the GCD):
-
Find the GCD of 18 and 24 using the Euclidean algorithm:
- 24 ÷ 18 = 1 remainder 6
- 18 ÷ 6 = 3 remainder 0
- GCD(18, 24) = 6
-
Apply the formula: LCM(18, 24) x GCD(18, 24) = 18 x 24 LCM(18, 24) x 6 = 432 LCM(18, 24) = 72
As you can see, the prime factorization method and the LCM/GCD relationship method are significantly more efficient for larger numbers.
Frequently Asked Questions (FAQ)
-
Q: What if the two numbers have no common factors other than 1? A: If the GCD of two numbers is 1 (they are relatively prime or coprime), then their LCM is simply the product of the two numbers. This is the case with 4 and 7, as their GCD is 1, and their LCM is 4 x 7 = 28.
-
Q: Can I find the LCM of more than two numbers? A: Yes, you can extend the prime factorization method or the GCD-based method to find the LCM of multiple numbers. For prime factorization, you consider all the prime factors involved and take the highest power of each.
-
Q: Is there a way to calculate the LCM using a calculator? A: Many scientific calculators have built-in functions to compute the LCM and GCD of numbers. Check your calculator's manual for instructions.
Conclusion
Finding the least common multiple is a fundamental skill in mathematics with broad applications. While the method of listing multiples is suitable for smaller numbers, the prime factorization method and the method utilizing the relationship between LCM and GCD prove far more efficient and effective, especially when dealing with larger numbers. Understanding these methods empowers you to tackle a wider range of mathematical problems and appreciate the interconnectedness of mathematical concepts. Mastering the LCM opens doors to deeper understanding in various fields, from fractions and algebra to more advanced mathematical concepts. So, practice these methods, and you'll find yourself confidently calculating LCMs for any pair of numbers you encounter!
Latest Posts
Latest Posts
-
X Or Y Dependent Variable
Sep 24, 2025
-
What Is Brass Made Of
Sep 24, 2025
-
Seven Characteristics Of Living Things
Sep 24, 2025
-
Mean From A Frequency Table
Sep 24, 2025
-
Reaction Of Metals With Water
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about Lcm For 4 And 7 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.