Lcm 3 5 And 6
dulhadulhi
Sep 25, 2025 · 6 min read
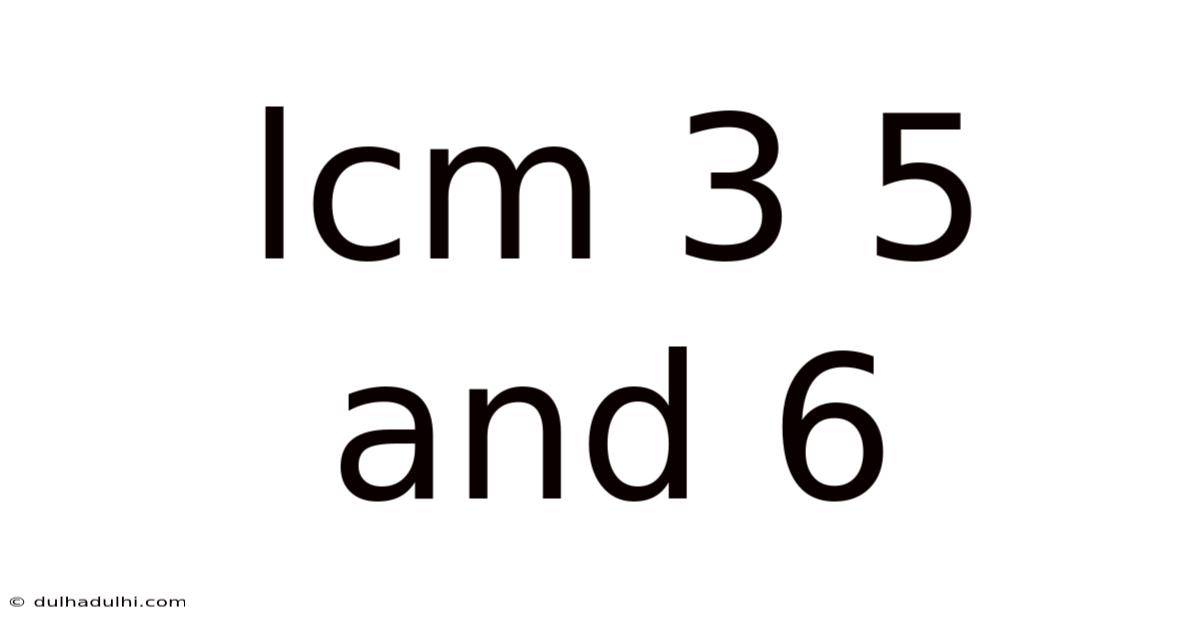
Table of Contents
Finding the Least Common Multiple (LCM) of 3, 5, and 6: A Comprehensive Guide
Finding the least common multiple (LCM) of a set of numbers is a fundamental concept in mathematics, crucial for solving various problems in arithmetic, algebra, and beyond. This comprehensive guide will walk you through understanding and calculating the LCM of 3, 5, and 6, explaining the process in detail and exploring different methods. We'll cover the definition of LCM, explore various calculation methods, and even delve into the underlying mathematical principles. By the end, you'll not only know the LCM of 3, 5, and 6 but also possess a robust understanding of this essential mathematical concept.
Understanding Least Common Multiple (LCM)
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers. In simpler terms, it's the smallest number that contains all the numbers in your set as factors. For example, if you consider the numbers 2 and 3, their multiples are:
- Multiples of 2: 2, 4, 6, 8, 10, 12, 14, 16, 18…
- Multiples of 3: 3, 6, 9, 12, 15, 18…
The smallest number that appears in both lists is 6. Therefore, the LCM of 2 and 3 is 6. This concept extends to sets of more than two numbers.
Method 1: Listing Multiples
This is a straightforward method, particularly useful for smaller numbers. Let's apply it to find the LCM of 3, 5, and 6:
-
List the multiples of each number:
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33...
- Multiples of 5: 5, 10, 15, 20, 25, 30, 35...
- Multiples of 6: 6, 12, 18, 24, 30, 36...
-
Identify common multiples: Observe that 30 is the smallest number that appears in all three lists.
-
Conclusion: Therefore, the LCM of 3, 5, and 6 is 30.
While this method is intuitive, it becomes less efficient with larger numbers or a greater number of integers.
Method 2: Prime Factorization
This is a more efficient and robust method, particularly useful for larger numbers. It leverages the fundamental theorem of arithmetic, which states that every integer greater than 1 can be uniquely represented as a product of prime numbers.
-
Find the prime factorization of each number:
- 3 = 3 (3 is a prime number)
- 5 = 5 (5 is a prime number)
- 6 = 2 × 3
-
Identify the highest power of each prime factor: Examine the prime factors from all the numbers. The prime factors involved are 2, 3, and 5. The highest power of each is:
- 2¹
- 3¹
- 5¹
-
Multiply the highest powers together: Multiply these highest powers to find the LCM: 2¹ × 3¹ × 5¹ = 30
-
Conclusion: The LCM of 3, 5, and 6 is 30.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and GCD (greatest common divisor) are closely related. There's a formula that links them:
LCM(a, b) × GCD(a, b) = a × b
This formula can be extended to more than two numbers, although the calculation becomes more complex. Let's see how this works for two numbers first, then consider extending to three:
For two numbers, say 'a' and 'b':
- Find the GCD of 3 and 5: The GCD(3, 5) = 1 (since 3 and 5 have no common factors other than 1)
- Apply the formula: LCM(3, 5) × GCD(3, 5) = 3 × 5 => LCM(3, 5) × 1 = 15 => LCM(3, 5) = 15
Now, let's find the LCM(15,6) using the same method
- Find the GCD of 15 and 6: The GCD(15, 6) = 3
- Apply the formula: LCM(15, 6) × GCD(15, 6) = 15 × 6 => LCM(15, 6) × 3 = 90 => LCM(15, 6) = 30
This shows that the LCM(3, 5, 6) = 30
While this method is mathematically elegant, it requires calculating the GCD first, which might add computational steps. For a larger set of numbers, the prime factorization method is usually more efficient.
Mathematical Explanation and Properties of LCM
The LCM's importance stems from its inherent properties and its applications in various mathematical contexts. Here are some key aspects:
-
Divisibility: The LCM of a set of numbers is divisible by each of the numbers in the set. This property is fundamental to many applications, including simplifying fractions and solving problems involving ratios and proportions.
-
Unique Representation: For a given set of numbers, there exists only one LCM. This uniqueness makes the LCM a well-defined and reliable mathematical concept.
-
Connection to GCD: As shown earlier, the LCM and GCD are intimately related through the formula: LCM(a, b) × GCD(a, b) = a × b. This relationship is a cornerstone of number theory.
-
Applications: LCMs are crucial in various mathematical areas, including:
- Fraction Addition and Subtraction: Finding a common denominator for fractions often involves determining the LCM of the denominators.
- Modular Arithmetic: LCMs play a vital role in solving problems related to congruences and modular arithmetic.
- Scheduling Problems: Consider scenarios where events need to occur at regular intervals. LCM helps determine when events coincide. For example, if bus A arrives every 3 minutes and bus B every 5 minutes, when will they both arrive at the same time? The answer is the LCM(3,5) = 15 minutes.
Frequently Asked Questions (FAQ)
Q1: Why is the LCM important?
A1: The LCM is crucial because it allows us to find the smallest common multiple for a set of numbers. This is vital in various applications, from simplifying fractions to solving complex mathematical problems and even real-world scheduling scenarios.
Q2: Can the LCM of two numbers be one of the numbers?
A2: Yes. If one number is a multiple of the other, the LCM will be the larger number. For example, LCM(2, 4) = 4.
Q3: Is there a formula for finding the LCM of more than two numbers?
A3: While there isn't a single concise formula like the one for two numbers, the prime factorization method remains the most effective way to find the LCM of any number of integers. You identify the highest power of each distinct prime factor present in the numbers and then multiply them together.
Q4: What if I have very large numbers?
A4: For very large numbers, using a calculator or computer software with built-in LCM functions is recommended. These tools efficiently handle the prime factorization and calculations involved.
Conclusion
Finding the least common multiple is a fundamental skill in mathematics. We’ve explored three different methods – listing multiples, prime factorization, and using the GCD – to determine the LCM of 3, 5, and 6, which is 30. The prime factorization method is generally the most efficient and versatile for a wide range of numbers. Understanding LCM is not just about calculation; it's about grasping the underlying mathematical principles and appreciating its wide-ranging applications in various fields. By mastering this concept, you'll equip yourself with a powerful tool for tackling diverse mathematical challenges. Remember to choose the method best suited to the numbers you are working with – for smaller numbers, the listing method might suffice, but for larger numbers, prime factorization is a far more efficient and reliable technique.
Latest Posts
Latest Posts
-
What Is 0 2 In Fraction
Sep 25, 2025
-
How Long Is 3 Miles
Sep 25, 2025
-
Where Does Diffusion Take Place
Sep 25, 2025
-
Repeating Decimal To Fraction Calculator
Sep 25, 2025
-
Regular Polygon And Irregular Polygon
Sep 25, 2025
Related Post
Thank you for visiting our website which covers about Lcm 3 5 And 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.