Is 2/3 Bigger Than 1/4
dulhadulhi
Sep 23, 2025 · 5 min read
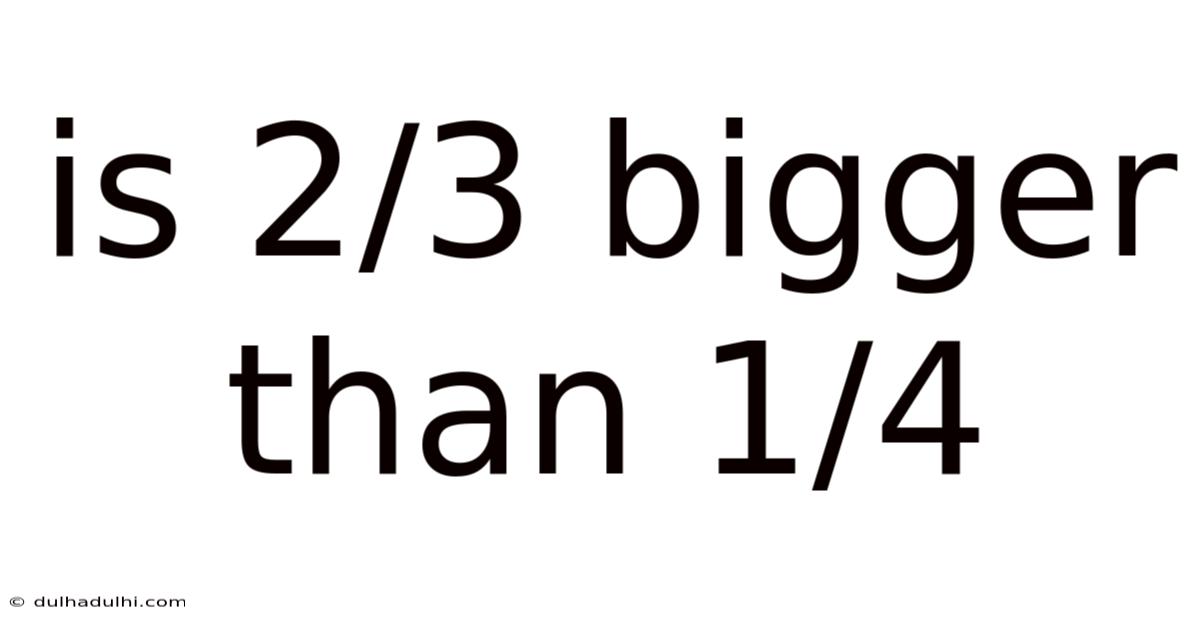
Table of Contents
Is 2/3 Bigger Than 1/4? A Deep Dive into Fraction Comparison
Understanding fractions is a fundamental skill in mathematics, crucial for everyday life and advanced studies. This article will comprehensively explore the question: "Is 2/3 bigger than 1/4?" We'll not only answer this specific question but also delve into the underlying concepts of fraction comparison, providing you with the tools to confidently compare any two fractions. We'll cover multiple methods, address common misconceptions, and offer practical examples to solidify your understanding.
Understanding Fractions: A Quick Refresher
Before we dive into the comparison, let's briefly revisit the concept of fractions. A fraction represents a part of a whole. It's written as a/b, where 'a' is the numerator (the number of parts we have) and 'b' is the denominator (the total number of equal parts the whole is divided into).
For example, in the fraction 2/3, the numerator (2) indicates we have two parts, and the denominator (3) means the whole is divided into three equal parts.
Method 1: Visual Comparison
One of the easiest ways to compare fractions is through visualization. Imagine two identical pies.
- Pie 1: Cut into three equal slices. Take two slices (2/3).
- Pie 2: Cut into four equal slices. Take one slice (1/4).
Looking at the two pies, it's visually apparent that two-thirds of Pie 1 is significantly larger than one-quarter of Pie 2. This visual method is excellent for building intuitive understanding, especially for beginners.
Method 2: Finding a Common Denominator
This is a more formal and widely applicable method. To compare fractions, we need to express them with the same denominator. This common denominator is a multiple of both denominators.
Steps:
-
Find the least common multiple (LCM) of the denominators: For 2/3 and 1/4, the denominators are 3 and 4. The LCM of 3 and 4 is 12.
-
Convert the fractions to equivalent fractions with the common denominator:
- To convert 2/3 to a fraction with a denominator of 12, we multiply both the numerator and denominator by 4: (2 * 4) / (3 * 4) = 8/12.
- To convert 1/4 to a fraction with a denominator of 12, we multiply both the numerator and denominator by 3: (1 * 3) / (4 * 3) = 3/12.
-
Compare the numerators: Now that both fractions have the same denominator, we can directly compare their numerators. Since 8 > 3, we conclude that 8/12 (or 2/3) is greater than 3/12 (or 1/4).
Method 3: Converting to Decimals
Another effective method is converting fractions to decimals. This involves dividing the numerator by the denominator.
- 2/3: 2 ÷ 3 ≈ 0.667
- 1/4: 1 ÷ 4 = 0.25
By comparing the decimal values, we see that 0.667 > 0.25, confirming that 2/3 is larger than 1/4. This method is particularly useful when dealing with fractions that are difficult to visualize or find a common denominator for easily.
Method 4: Using Cross-Multiplication
This method is a shortcut for comparing fractions without finding a common denominator.
Steps:
-
Cross-multiply: Multiply the numerator of the first fraction by the denominator of the second fraction, and vice versa.
- 2/3 and 1/4: (2 * 4) = 8 and (3 * 1) = 3
-
Compare the products: The larger product corresponds to the larger fraction. Since 8 > 3, 2/3 is greater than 1/4.
This method is efficient, but it's crucial to remember to correctly identify which product corresponds to which fraction.
Addressing Common Misconceptions
-
Larger denominator means smaller fraction: This is a common mistake. While it's true for fractions with the same numerator (e.g., 1/2 > 1/4), it's not universally applicable. Comparing fractions requires considering both the numerator and the denominator.
-
Ignoring the context: The size of a fraction always depends on the context. 2/3 of a pizza is much larger than 1/4 of a pizza, but 2/3 of a small cupcake might be smaller than 1/4 of a large cake. Always remember the whole to which the fraction refers.
Beyond the Basics: Working with Mixed Numbers and Improper Fractions
The methods discussed above can be extended to mixed numbers (e.g., 1 1/2) and improper fractions (where the numerator is larger than the denominator, e.g., 5/4).
-
Mixed Numbers: Convert mixed numbers to improper fractions before comparing them using any of the methods described. For example, 1 1/2 = 3/2.
-
Improper Fractions: These can be compared using the same techniques as proper fractions. You can also convert them to mixed numbers for easier visualization.
Real-World Applications
Understanding fraction comparison is vital in many real-world situations:
-
Cooking: Following recipes often involves measuring ingredients using fractions (e.g., 1/2 cup of flour, 2/3 cup of sugar).
-
Construction: Precision in construction relies heavily on accurate measurements, often expressed as fractions of inches or feet.
-
Finance: Calculating percentages, interest rates, and proportions all involve working with fractions.
-
Data Analysis: Interpreting data presented as fractions or proportions is essential in many fields.
Frequently Asked Questions (FAQs)
Q: Can I always use the common denominator method?
A: Yes, the common denominator method is a reliable and universally applicable technique for comparing fractions.
Q: Is cross-multiplication always the fastest method?
A: While often quicker, cross-multiplication can be prone to errors if not performed carefully. The common denominator method offers a more systematic approach.
Q: What if the fractions have very large denominators?
A: For fractions with very large denominators, using a calculator to convert to decimals can be the most efficient approach.
Q: How can I improve my understanding of fractions?
A: Practice is key! Work through various examples, utilize visual aids, and try different comparison methods to build confidence and proficiency.
Conclusion
In conclusion, 2/3 is definitively bigger than 1/4. This article explored multiple methods to prove this, emphasizing the importance of understanding the underlying principles of fraction comparison. Mastering these techniques will not only allow you to accurately compare fractions but also equip you with a crucial mathematical skill applicable across various aspects of life. Remember to practice regularly and choose the method that best suits your understanding and the complexity of the fractions involved. Don't hesitate to revisit the different approaches until you feel confident in your ability to compare any two fractions accurately and efficiently.
Latest Posts
Latest Posts
-
How Was Mt Everest Formed
Sep 24, 2025
-
Words With The Inter Prefix
Sep 24, 2025
-
300 Sq Ft To Meters
Sep 24, 2025
-
Highest Tide In The World
Sep 24, 2025
-
1 68 M In Feet
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about Is 2/3 Bigger Than 1/4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.