Hcf Of 48 And 80
dulhadulhi
Sep 21, 2025 · 7 min read
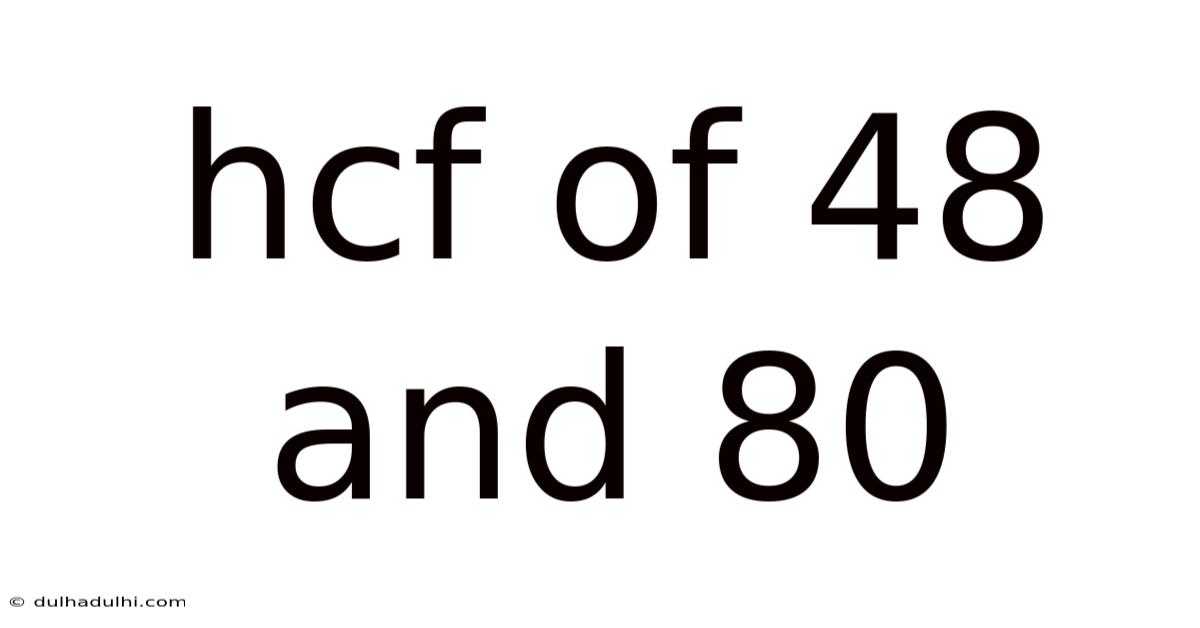
Table of Contents
Finding the Highest Common Factor (HCF) of 48 and 80: A Comprehensive Guide
Finding the Highest Common Factor (HCF), also known as the Greatest Common Divisor (GCD), of two numbers is a fundamental concept in mathematics. Understanding HCF is crucial for simplifying fractions, solving problems in algebra, and tackling more advanced mathematical concepts. This article will provide a comprehensive guide to finding the HCF of 48 and 80, exploring multiple methods and delving into the underlying mathematical principles. We'll cover everything from the basic prime factorization method to more advanced techniques, ensuring you gain a solid understanding of this important topic.
Introduction to Highest Common Factor (HCF)
The Highest Common Factor (HCF) of two or more numbers is the largest number that divides each of them without leaving a remainder. In simpler terms, it's the biggest number that's a factor of both numbers. For example, the HCF of 12 and 18 is 6 because 6 is the largest number that divides both 12 and 18 evenly. Understanding HCF is vital in various mathematical applications, from simplifying fractions to solving algebraic equations. This article will focus on finding the HCF of 48 and 80, illustrating various methods and explaining the reasoning behind them.
Method 1: Prime Factorization
The prime factorization method is a classic and reliable way to find the HCF of two numbers. It involves breaking down each number into its prime factors – numbers divisible only by 1 and themselves. Let's apply this method to find the HCF of 48 and 80:
Step 1: Find the prime factorization of 48.
48 can be broken down as follows:
48 = 2 x 24 = 2 x 2 x 12 = 2 x 2 x 2 x 6 = 2 x 2 x 2 x 2 x 3 = 2<sup>4</sup> x 3
Step 2: Find the prime factorization of 80.
80 can be broken down as follows:
80 = 2 x 40 = 2 x 2 x 20 = 2 x 2 x 2 x 10 = 2 x 2 x 2 x 2 x 5 = 2<sup>4</sup> x 5
Step 3: Identify common prime factors.
Comparing the prime factorizations of 48 and 80, we see that they both share four factors of 2:
48 = 2<sup>4</sup> x 3 80 = 2<sup>4</sup> x 5
Step 4: Calculate the HCF.
The HCF is the product of the common prime factors raised to the lowest power. In this case, the only common prime factor is 2, and the lowest power is 2<sup>4</sup>. Therefore:
HCF(48, 80) = 2<sup>4</sup> = 16
Therefore, the highest common factor of 48 and 80 is 16.
Method 2: Listing Factors
This method involves listing all the factors of each number and then identifying the largest common factor. While simpler for smaller numbers, it becomes less efficient for larger numbers.
Step 1: List the factors of 48.
The factors of 48 are: 1, 2, 3, 4, 6, 8, 12, 16, 24, 48
Step 2: List the factors of 80.
The factors of 80 are: 1, 2, 4, 5, 8, 10, 16, 20, 40, 80
Step 3: Identify common factors.
Comparing the two lists, we find the common factors: 1, 2, 4, 8, 16
Step 4: Determine the HCF.
The largest common factor is 16. Therefore, the HCF of 48 and 80 is 16.
Method 3: Euclidean Algorithm
The Euclidean Algorithm is a highly efficient method for finding the HCF of two numbers, especially when dealing with larger numbers. It's based on the principle that the HCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the HCF.
Step 1: Divide the larger number (80) by the smaller number (48).
80 ÷ 48 = 1 with a remainder of 32.
Step 2: Replace the larger number with the remainder.
Now we find the HCF of 48 and 32.
Step 3: Repeat the process.
48 ÷ 32 = 1 with a remainder of 16.
Step 4: Repeat again.
32 ÷ 16 = 2 with a remainder of 0.
Step 5: The HCF is the last non-zero remainder.
Since the remainder is 0, the HCF is the last non-zero remainder, which is 16. Therefore, the HCF(48, 80) = 16.
Mathematical Explanation of the Euclidean Algorithm
The Euclidean Algorithm's efficiency stems from its use of the division algorithm. The division algorithm states that for any two integers a and b (where b is not zero), there exist unique integers q and r such that:
a = bq + r, where 0 ≤ r < |b|
Here, a is the dividend, b is the divisor, q is the quotient, and r is the remainder. The Euclidean Algorithm repeatedly applies this algorithm, reducing the problem to finding the HCF of smaller numbers until a remainder of 0 is obtained. The last non-zero remainder is the HCF. This method is significantly faster than the prime factorization method for large numbers.
Applications of HCF
The concept of HCF has numerous applications in various fields:
-
Simplifying Fractions: To simplify a fraction to its lowest terms, we find the HCF of the numerator and denominator and divide both by it. For example, to simplify the fraction 48/80, we find the HCF (16) and simplify to 3/5.
-
Algebra: HCF is used in solving algebraic equations and simplifying algebraic expressions.
-
Measurement: HCF is useful in determining the largest possible size of square tiles that can be used to cover a rectangular floor without cutting any tiles.
-
Number Theory: HCF plays a significant role in various number theory concepts, including modular arithmetic and cryptography.
Frequently Asked Questions (FAQ)
Q1: What is the difference between HCF and LCM?
The Highest Common Factor (HCF) is the largest number that divides two or more numbers without leaving a remainder, while the Least Common Multiple (LCM) is the smallest number that is a multiple of two or more numbers. They are inversely related; for two numbers a and b, HCF(a, b) x LCM(a, b) = a x b.
Q2: Can the HCF of two numbers be greater than either number?
No. The HCF of two numbers can never be greater than either of the numbers. It is always less than or equal to the smaller of the two numbers.
Q3: What is the HCF of two prime numbers?
The HCF of two distinct prime numbers is always 1. Prime numbers are only divisible by 1 and themselves.
Q4: What if one of the numbers is 0?
The HCF of any number and 0 is undefined. However, if you consider the HCF in the context of the Euclidean algorithm, then it will return the other number as the HCF.
Q5: Are there any other methods to find HCF besides the ones mentioned?
Yes, there are other methods such as using Venn diagrams (particularly useful for visualizing the prime factorizations) or using repeated subtraction. However, the prime factorization method, listing factors and the Euclidean algorithm are the most commonly used and generally most efficient techniques.
Conclusion
Finding the Highest Common Factor (HCF) is a fundamental skill in mathematics with wide-ranging applications. We've explored three distinct methods – prime factorization, listing factors, and the Euclidean algorithm – each offering a unique approach to solving the problem. Understanding these methods provides a strong foundation for tackling more complex mathematical challenges. Remember that the most efficient method will depend on the size of the numbers involved; for larger numbers, the Euclidean Algorithm is generally preferred for its computational efficiency. Regardless of the method chosen, mastering the concept of HCF is essential for any student's mathematical journey. The HCF of 48 and 80, as demonstrated through various methods, is definitively 16. This understanding forms a bedrock for progressing into more advanced mathematical concepts and problem-solving.
Latest Posts
Latest Posts
-
Is Blue Or Brown Live
Sep 21, 2025
-
How Are Hen Eggs Fertilized
Sep 21, 2025
-
Diagram Of Destructive Plate Boundary
Sep 21, 2025
-
Static Pressure Vs Dynamic Pressure
Sep 21, 2025
-
Does Stress Cause Urine Infection
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about Hcf Of 48 And 80 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.