Hcf Of 24 And 40
dulhadulhi
Sep 21, 2025 · 6 min read
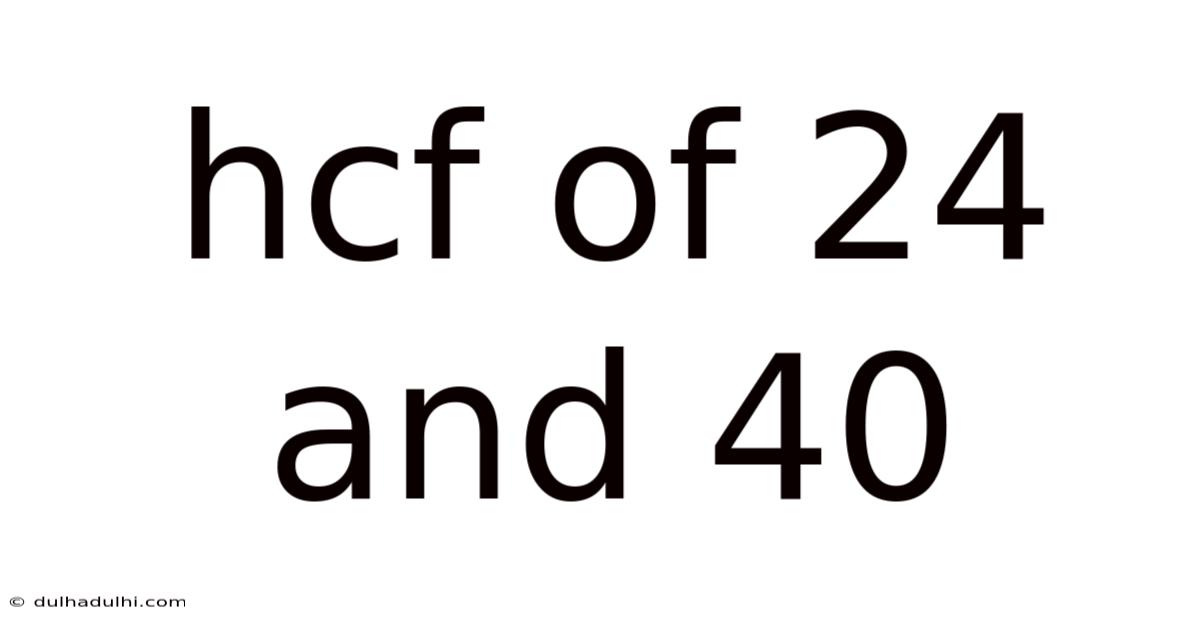
Table of Contents
Finding the Highest Common Factor (HCF) of 24 and 40: A Comprehensive Guide
Finding the Highest Common Factor (HCF), also known as the Greatest Common Divisor (GCD), of two numbers is a fundamental concept in mathematics. This comprehensive guide will explore various methods to determine the HCF of 24 and 40, explaining each step in detail and providing a deeper understanding of the underlying principles. We'll cover prime factorization, the Euclidean algorithm, and the listing factors method, ensuring you gain a robust understanding of this crucial mathematical concept. This will be useful for students learning about number theory, as well as anyone needing to refresh their understanding of HCF calculations.
Understanding Highest Common Factor (HCF)
The Highest Common Factor (HCF) of two or more numbers is the largest number that divides each of them without leaving a remainder. It's the biggest number that is a factor of all the numbers involved. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12. The factors of 18 are 1, 2, 3, 6, 9, and 18. The common factors of 12 and 18 are 1, 2, 3, and 6. The highest common factor is 6. This is what we aim to find for 24 and 40.
Method 1: Prime Factorization
This method involves breaking down each number into its prime factors. Prime numbers are numbers greater than 1 that are only divisible by 1 and themselves (e.g., 2, 3, 5, 7, 11, etc.).
Steps:
-
Find the prime factorization of 24: 24 = 2 x 12 = 2 x 2 x 6 = 2 x 2 x 2 x 3 = 2³ x 3¹
-
Find the prime factorization of 40: 40 = 2 x 20 = 2 x 2 x 10 = 2 x 2 x 2 x 5 = 2³ x 5¹
-
Identify common prime factors: Both 24 and 40 share three factors of 2 (2³).
-
Calculate the HCF: The HCF is the product of the common prime factors raised to the lowest power. In this case, it's 2³.
-
Result: 2³ = 8. Therefore, the HCF of 24 and 40 is 8.
This method is straightforward and provides a clear understanding of the underlying structure of the numbers. It is particularly useful when dealing with larger numbers where other methods might become cumbersome.
Method 2: Listing Factors
This method involves listing all the factors of each number and then identifying the common factors.
Steps:
-
List the factors of 24: 1, 2, 3, 4, 6, 8, 12, 24
-
List the factors of 40: 1, 2, 4, 5, 8, 10, 20, 40
-
Identify common factors: The common factors of 24 and 40 are 1, 2, 4, and 8.
-
Determine the HCF: The highest common factor among these is 8.
-
Result: The HCF of 24 and 40 is 8.
This method is simpler for smaller numbers but can become impractical for larger numbers with many factors.
Method 3: Euclidean Algorithm
The Euclidean algorithm is an efficient method for finding the HCF of two numbers, particularly useful for larger numbers. It's based on the principle that the HCF of two numbers does not change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the HCF.
Steps:
-
Divide the larger number (40) by the smaller number (24): 40 ÷ 24 = 1 with a remainder of 16.
-
Replace the larger number with the remainder: Now we find the HCF of 24 and 16.
-
Repeat the division: 24 ÷ 16 = 1 with a remainder of 8.
-
Repeat the division: 16 ÷ 8 = 2 with a remainder of 0.
-
Result: When the remainder is 0, the HCF is the last non-zero remainder, which is 8. Therefore, the HCF of 24 and 40 is 8.
The Euclidean algorithm is computationally efficient and avoids the need to find all factors, making it suitable for larger numbers.
Visualizing the HCF: Venn Diagrams
A Venn diagram can help visualize the common factors. We can represent the factors of 24 and 40 in two overlapping circles. The overlapping area represents the common factors.
- Factors of 24: 1, 2, 3, 4, 6, 8, 12, 24
- Factors of 40: 1, 2, 4, 5, 8, 10, 20, 40
The overlapping factors (common factors) are 1, 2, 4, and 8. The largest of these is 8, hence the HCF.
Applications of HCF
Understanding and calculating the HCF has various practical applications across different fields:
-
Simplifying Fractions: The HCF is used to simplify fractions to their lowest terms. For example, the fraction 24/40 can be simplified by dividing both the numerator and denominator by their HCF (8), resulting in the simplified fraction 3/5.
-
Solving Word Problems: Many word problems involving division and sharing require finding the HCF. For instance, if you have 24 apples and 40 oranges, and you want to distribute them into bags with equal numbers of apples and oranges in each bag, the maximum number of bags you can create is determined by the HCF of 24 and 40, which is 8. Each bag will contain 3 apples and 5 oranges.
-
Geometry: The HCF can be used in geometrical problems involving dividing shapes into smaller, identical shapes. For example, finding the largest square tile that can perfectly cover a rectangular floor of dimensions 24 units by 40 units involves determining the HCF of 24 and 40.
-
Number Theory: The HCF is a fundamental concept in number theory, forming the basis for many advanced mathematical theorems and algorithms.
Frequently Asked Questions (FAQ)
Q1: What if the HCF of two numbers is 1?
A1: If the HCF of two numbers is 1, the numbers are said to be relatively prime or coprime. This means they share no common factors other than 1.
Q2: Can the HCF of two numbers be greater than the smaller number?
A2: No, the HCF can never be greater than the smaller of the two numbers.
Q3: Are there other methods to find the HCF besides the ones mentioned?
A3: Yes, there are more advanced methods, such as the binary GCD algorithm, which is optimized for computer calculations. However, the methods discussed here provide a strong foundation for understanding the concept.
Q4: How do I find the HCF of more than two numbers?
A4: To find the HCF of more than two numbers, you can use any of the methods described above, but you'll apply them iteratively. For example, to find the HCF of 24, 40, and 60, you'd first find the HCF of 24 and 40 (which is 8), and then find the HCF of 8 and 60. The final result would be the HCF of all three numbers.
Conclusion
Finding the Highest Common Factor is a crucial skill in mathematics with various applications. We have explored three different methods – prime factorization, listing factors, and the Euclidean algorithm – each with its strengths and weaknesses. Understanding these methods allows you to choose the most appropriate approach based on the numbers involved. Remember that the HCF represents the largest common divisor, providing valuable insights into the relationship between numbers and offering practical solutions in various real-world scenarios. Mastering this concept lays a solid foundation for further explorations in number theory and related fields. The HCF of 24 and 40, as demonstrated by all three methods, is definitively 8. Now you are well-equipped to tackle any HCF challenge that comes your way!
Latest Posts
Latest Posts
-
Perimeter Of A Compound Shape
Sep 21, 2025
-
Wood Is A Fossil Fuel
Sep 21, 2025
-
Can Bumble Bees Make Honey
Sep 21, 2025
-
What Is A Natural Hazard
Sep 21, 2025
-
Circulatory System In A Fish
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about Hcf Of 24 And 40 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.