75/100 In Its Simplest Form
dulhadulhi
Sep 22, 2025 · 5 min read
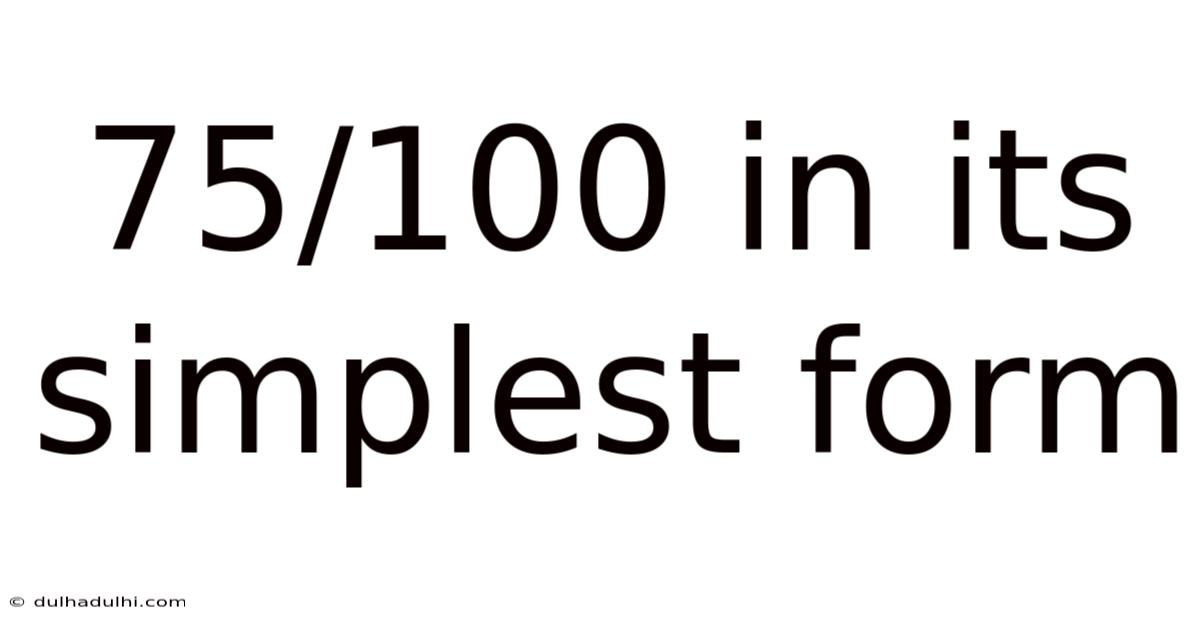
Table of Contents
75/100 in its Simplest Form: A Comprehensive Guide to Fraction Simplification
Understanding fractions is a fundamental skill in mathematics, applicable across numerous fields from baking to engineering. This article will delve into the process of simplifying fractions, specifically focusing on reducing 75/100 to its simplest form. We'll explore the concept, the steps involved, and even touch upon the broader mathematical principles behind fraction simplification. This guide is perfect for anyone looking to brush up on their fraction skills, from elementary school students to adults seeking to strengthen their foundational math understanding. By the end, you'll not only know the answer but also understand why and how we arrive at it.
Understanding Fractions: A Quick Recap
A fraction represents a part of a whole. It's written as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts we have, while the denominator indicates how many parts make up the whole. For example, in the fraction 75/100, 75 is the numerator and 100 is the denominator. This means we have 75 parts out of a possible 100 parts.
Simplifying a fraction, also known as reducing a fraction, means finding an equivalent fraction where the numerator and denominator are smaller numbers, but the fraction still represents the same value. This makes the fraction easier to understand and work with.
Finding the Greatest Common Divisor (GCD)
The key to simplifying fractions lies in finding the Greatest Common Divisor (GCD), also known as the Greatest Common Factor (GCF), of the numerator and denominator. The GCD is the largest number that divides both the numerator and the denominator without leaving a remainder.
There are several ways to find the GCD:
-
Listing Factors: List all the factors (numbers that divide evenly) of both the numerator and the denominator. Then, identify the largest factor they have in common. For example, the factors of 75 are 1, 3, 5, 15, 25, and 75. The factors of 100 are 1, 2, 4, 5, 10, 20, 25, 50, and 100. The largest common factor is 25.
-
Prime Factorization: This method involves breaking down both numbers into their prime factors (numbers divisible only by 1 and themselves). Then, identify the common prime factors and multiply them together.
Let's use prime factorization for 75 and 100:
- 75 = 3 x 5 x 5 = 3 x 5²
- 100 = 2 x 2 x 5 x 5 = 2² x 5²
The common prime factors are 5 and 5 (or 5²). Therefore, the GCD is 5 x 5 = 25.
-
Euclidean Algorithm: This is a more efficient method for larger numbers. It involves repeatedly dividing the larger number by the smaller number and replacing the larger number with the remainder until the remainder is 0. The last non-zero remainder is the GCD. While effective, it’s perhaps less intuitive for simpler fractions like 75/100.
Simplifying 75/100: Step-by-Step
Now that we understand how to find the GCD, let's simplify 75/100:
-
Find the GCD: As we determined above, the GCD of 75 and 100 is 25.
-
Divide the Numerator and Denominator by the GCD: Divide both the numerator (75) and the denominator (100) by the GCD (25):
- 75 ÷ 25 = 3
- 100 ÷ 25 = 4
-
Write the Simplified Fraction: The simplified fraction is 3/4.
Therefore, 75/100 in its simplest form is 3/4.
Visual Representation of Fraction Simplification
Imagine a pizza cut into 100 slices. 75/100 represents having 75 of those slices. If we group the slices into sets of 25, we have 3 sets of 25 slices out of a total of 4 sets of 25 slices. This visually demonstrates that 75/100 is equivalent to 3/4.
Further Exploration: Equivalent Fractions
It's important to understand that a fraction can have multiple equivalent forms. For example, 75/100, 150/200, and 300/400 all represent the same value (0.75 or 75%). Simplifying a fraction ensures we are working with the most concise and manageable representation.
Real-World Applications of Fraction Simplification
Fraction simplification isn't just an abstract mathematical exercise. It's a practical skill used in various real-world scenarios:
- Baking: Recipes often use fractions. Simplifying fractions helps in accurate measurements.
- Construction: Precise measurements are crucial, and simplified fractions make calculations easier.
- Finance: Working with percentages (which are essentially fractions) requires understanding fraction simplification for accurate calculations of interest, discounts, and more.
- Data Analysis: In various fields, data is often represented using fractions, and simplification helps in data interpretation.
Frequently Asked Questions (FAQ)
Q: What if I don't find the greatest common divisor right away?
A: Even if you don't find the GCD immediately, you can simplify the fraction in steps. For example, you could divide both the numerator and denominator by 5, resulting in 15/20. Then, you could further simplify by dividing by 5 again, arriving at 3/4. While this takes longer, it still leads to the correct simplified form.
Q: Can I simplify a fraction if the numerator is larger than the denominator?
A: Yes. Such fractions are called improper fractions. You can simplify them in the same way as proper fractions (numerator smaller than denominator). You can also convert improper fractions into mixed numbers (a whole number and a fraction).
Q: Are there any online tools to help with simplifying fractions?
A: While this article aims to empower you to simplify fractions independently, various online calculators and websites are available that can simplify fractions automatically. However, understanding the underlying process is vital for genuine mathematical understanding.
Q: What happens if the GCD is 1?
A: If the GCD of the numerator and denominator is 1, the fraction is already in its simplest form. This means there are no common factors other than 1.
Conclusion
Simplifying fractions, like reducing 75/100 to its simplest form of 3/4, is a core concept in mathematics with wide-ranging practical applications. By understanding the process of finding the greatest common divisor and applying the appropriate division, you can confidently simplify any fraction, enhancing your mathematical skills and making calculations easier and more efficient in various contexts. Remember, mastering this skill isn't just about getting the right answer; it's about grasping the underlying mathematical principles and their practical relevance. Practice makes perfect, so try simplifying different fractions to build your confidence and proficiency.
Latest Posts
Latest Posts
-
Do Bumble Bees Make Honey
Sep 22, 2025
-
Truth Table From Logic Circuit
Sep 22, 2025
-
0 4 Recurring As A Fraction
Sep 22, 2025
-
How Many Inches Is 300mm
Sep 22, 2025
-
How To Reduce Pool Chlorine
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 75/100 In Its Simplest Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.