5 9 As A Percentage
dulhadulhi
Sep 22, 2025 · 5 min read
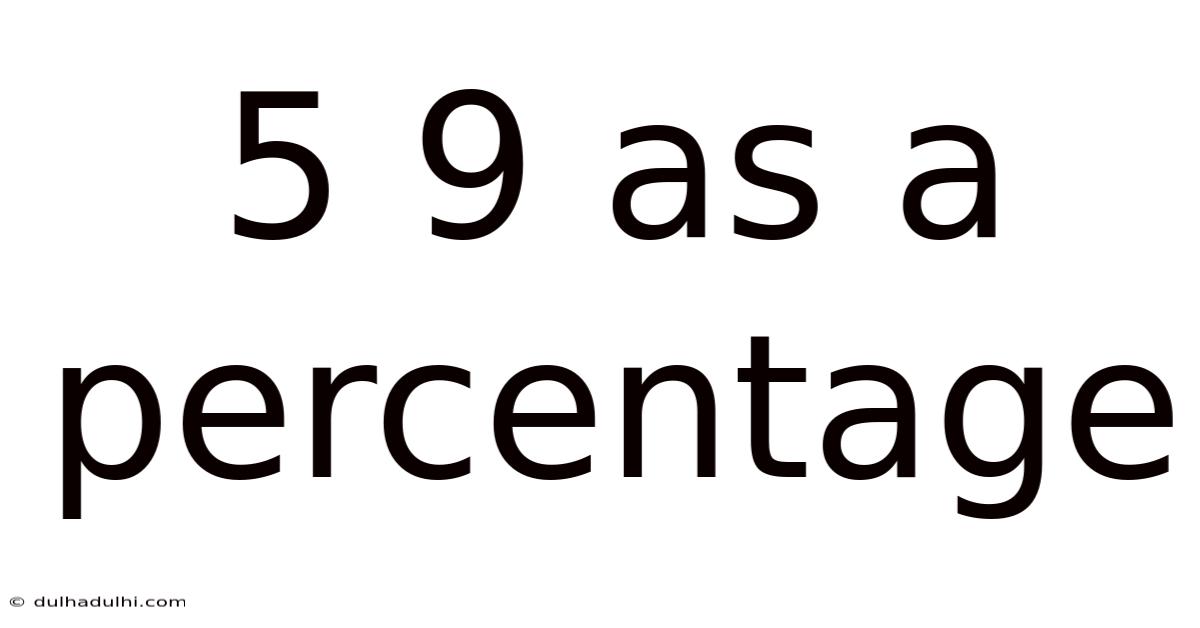
Table of Contents
Understanding 5/9 as a Percentage: A Comprehensive Guide
Expressing fractions as percentages is a fundamental skill in mathematics with widespread applications in daily life, from calculating discounts to understanding statistics. This article provides a comprehensive guide to understanding how to convert the fraction 5/9 into a percentage, along with explanations, examples, and frequently asked questions. We'll delve into the underlying mathematical principles, ensuring you gain a firm grasp of this essential concept. Understanding percentages is crucial for various fields, from finance and economics to science and everyday budgeting.
What is a Percentage?
A percentage is a way of expressing a number as a fraction of 100. The word "percent" comes from the Latin "per centum," meaning "out of a hundred." Therefore, 50% means 50 out of 100, or 50/100, which simplifies to 1/2. Percentages are used to represent proportions or ratios, making it easier to compare different values or quantities.
Converting Fractions to Percentages: The Method
Converting a fraction to a percentage involves two main steps:
-
Convert the fraction to a decimal: Divide the numerator (the top number) by the denominator (the bottom number).
-
Convert the decimal to a percentage: Multiply the decimal by 100 and add the "%" symbol.
Calculating 5/9 as a Percentage
Let's apply these steps to convert the fraction 5/9 into a percentage:
-
Convert 5/9 to a decimal:
5 ÷ 9 = 0.55555... (This is a repeating decimal)
-
Convert the decimal to a percentage:
0.55555... × 100 = 55.555...%
Therefore, 5/9 is approximately equal to 55.56%. We round to two decimal places for practical purposes.
Understanding Repeating Decimals
The conversion of 5/9 to a decimal results in a repeating decimal (0.555...). This means the digit 5 repeats infinitely. In practical applications, we usually round the decimal to a certain number of decimal places. The level of precision required depends on the context. For most everyday calculations, rounding to two decimal places (55.56%) is sufficient. However, in scientific or engineering applications, more decimal places might be necessary for accuracy.
Alternative Method: Using Proportions
Another approach to converting 5/9 to a percentage involves setting up a proportion. We know that a percentage is a fraction out of 100. Therefore, we can set up the following proportion:
5/9 = x/100
To solve for 'x' (the percentage), we can cross-multiply:
9x = 500
x = 500/9
x ≈ 55.56
This method confirms our previous calculation.
Practical Applications of Percentage Conversions
Understanding how to convert fractions to percentages is essential in various real-world situations:
-
Discounts: A store offering a 25% discount on an item means you pay 75% of the original price.
-
Taxes: Sales tax is usually expressed as a percentage of the purchase price.
-
Grades: School grades are often expressed as percentages.
-
Statistics: Data is frequently presented in the form of percentages to make it easier to understand and compare.
-
Financial Calculations: Interest rates, loan repayments, and investment returns are all expressed as percentages.
-
Surveys and Polls: Results are often presented as percentages to show the proportion of respondents who chose a particular option.
More Examples of Fraction to Percentage Conversions
Let's explore a few more examples to reinforce your understanding:
-
1/4 as a percentage: 1 ÷ 4 = 0.25; 0.25 × 100 = 25%
-
3/5 as a percentage: 3 ÷ 5 = 0.6; 0.6 × 100 = 60%
-
2/3 as a percentage: 2 ÷ 3 = 0.666...; 0.666... × 100 ≈ 66.67%
-
7/8 as a percentage: 7 ÷ 8 = 0.875; 0.875 × 100 = 87.5%
Advanced Concepts: Percentage Increase and Decrease
Beyond basic conversion, understanding percentage changes is crucial. A percentage increase or decrease shows the relative change between two values.
-
Percentage Increase: [(New Value - Old Value) / Old Value] × 100
-
Percentage Decrease: [(Old Value - New Value) / Old Value] × 100
For example, if a price increases from $10 to $12, the percentage increase is:
[(12 - 10) / 10] × 100 = 20%
Frequently Asked Questions (FAQ)
Q1: Why is 5/9 a repeating decimal?
A1: A repeating decimal occurs when the denominator of a fraction cannot be expressed as a product of only 2s and 5s (the factors of 10). Since 9 has factors other than 2 and 5, the decimal representation of 5/9 is a repeating decimal.
Q2: How accurate does my percentage calculation need to be?
A2: The required accuracy depends on the context. For everyday calculations, rounding to two decimal places is usually sufficient. However, in scientific or financial contexts, higher precision might be necessary.
Q3: Can I use a calculator to convert fractions to percentages?
A3: Yes, most calculators have the functionality to perform these conversions. Simply divide the numerator by the denominator and then multiply by 100.
Q4: What if I have a mixed number (e.g., 1 2/3)? How do I convert it to a percentage?
A4: First, convert the mixed number into an improper fraction. For example, 1 2/3 becomes 5/3. Then, follow the standard steps for converting a fraction to a percentage. 5/3 = 1.666...; 1.666... × 100 ≈ 166.67%
Q5: Are there online tools to help with percentage calculations?
A5: Yes, many online calculators and converters are available that can help with various percentage calculations, including fraction to percentage conversions.
Conclusion
Converting fractions to percentages is a fundamental mathematical skill with many real-world applications. Understanding the underlying principles and methods, such as dividing the numerator by the denominator and multiplying by 100, allows for accurate calculations. Remember to consider the context when determining the level of precision needed for rounding. Mastering this skill empowers you to confidently handle various percentage-related tasks in various aspects of your life, from personal finance to professional endeavors. Practice regularly with different fractions to build your proficiency and understanding.
Latest Posts
Latest Posts
-
Is 8 A Cube Number
Sep 22, 2025
-
What Is A Co Ordinate Bond
Sep 22, 2025
-
Highest Common Factor Of 30
Sep 22, 2025
-
Proof Of Arithmetic Series Sum
Sep 22, 2025
-
Capacitors In Parallel Vs Series
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 5 9 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.