3 Divided By 5 8
dulhadulhi
Sep 21, 2025 · 6 min read
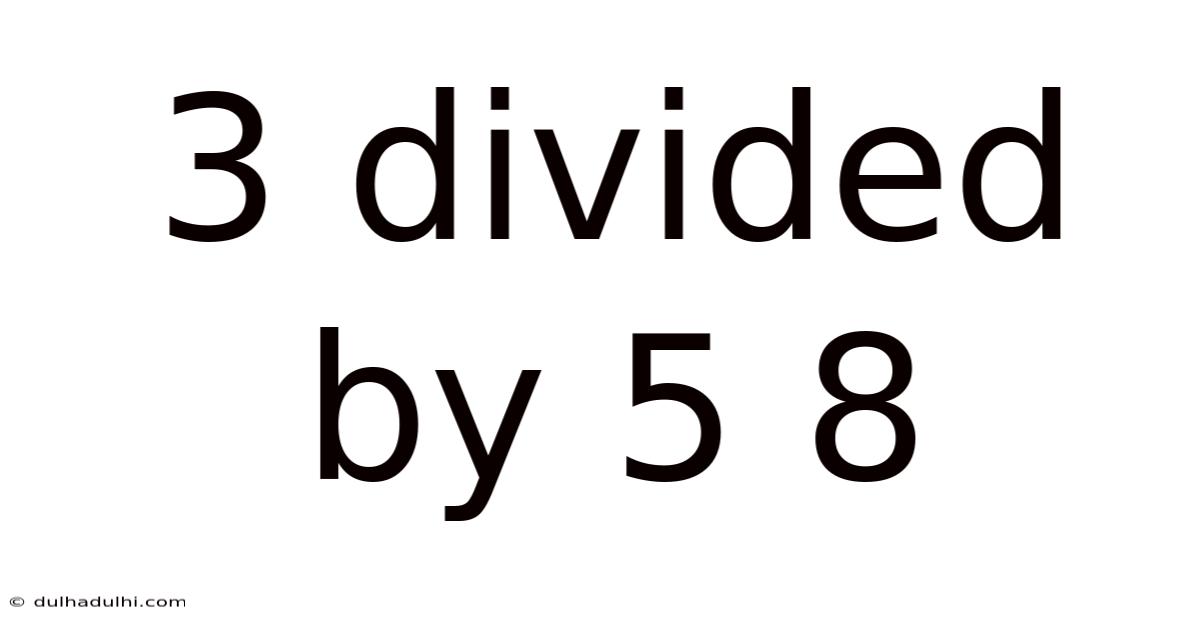
Table of Contents
Decoding 3 Divided by 58: A Deep Dive into Division and Decimal Representation
This article explores the seemingly simple yet conceptually rich problem of 3 divided by 58. We'll delve beyond the immediate answer to unpack the underlying principles of division, explore different methods of solving this problem, understand the significance of decimal representation, and address common misconceptions. This comprehensive guide is designed for anyone seeking a clear and thorough understanding of this fundamental mathematical operation. The concepts explored will be valuable for students of various ages and backgrounds, from elementary school to those brushing up on their mathematical skills.
Introduction: Understanding Division
Division is one of the four basic arithmetic operations, alongside addition, subtraction, and multiplication. It's the process of determining how many times one number (the divisor) goes into another number (the dividend). The result is called the quotient. In our case, we have 3 (dividend) divided by 58 (divisor). This immediately suggests that the quotient will be less than 1, as 58 is significantly larger than 3. This situation necessitates understanding decimal representation – a crucial concept in mathematics.
Method 1: Long Division
The traditional method for solving this problem is long division. While it might seem daunting at first, long division provides a systematic approach that helps visualize the division process.
-
Setup: Write the dividend (3) inside the long division symbol and the divisor (58) outside. Since 3 is smaller than 58, we'll need to add a decimal point to 3 and add zeros as needed. This doesn't change the value of 3, but allows us to continue the division process.
-
Decimal Point: Add a decimal point after the 3 and add a zero to make it 3.0. This doesn’t change the value. Bring the decimal point up into the quotient.
-
Iteration: Now we ask, how many times does 58 go into 30? The answer is zero. Write a 0 above the 0 in 3.0.
-
Adding Zeros: Add another zero to make it 3.00. Now, how many times does 58 go into 300? 58 x 5 = 290. Write a 5 above the second 0 in the quotient.
-
Subtraction: Subtract 290 from 300. This leaves a remainder of 10.
-
Continue: Add another zero to make it 100. How many times does 58 go into 100? 58 x 1 = 58. Write a 1 above the third zero in the quotient.
-
Repeat: Subtract 58 from 100. This leaves a remainder of 42. Continue this process of adding zeros, dividing, and subtracting until you reach a desired level of accuracy or a repeating pattern emerges.
Following this method, we'll find that 3 divided by 58 is approximately 0.051724... The process continues indefinitely, resulting in a non-terminating decimal.
Method 2: Using a Calculator
A calculator provides a quick and efficient way to obtain the answer. Simply enter 3 ÷ 58 and the calculator will provide the decimal approximation. While convenient, it's important to understand the underlying mathematical process, which long division elucidates.
Understanding Decimal Representation
The result of 3 divided by 58 is a non-terminating, non-repeating decimal. This means the decimal representation goes on forever without a repeating pattern. This is in contrast to fractions like 1/4 (0.25) which have terminating decimal representations, and fractions like 1/3 (0.333...) which have repeating decimal representations.
The non-terminating nature of the decimal representation highlights the limitations of using decimal representation to fully express certain rational numbers. It also introduces the concept of approximation. In practical applications, we often round the decimal to a certain number of decimal places depending on the required level of precision.
Fraction Representation
Alternatively, we can express the result as a fraction: 3/58. This fraction is in its simplest form and accurately represents the result without any loss of information or approximation. While a decimal representation can be useful for calculations and comparisons, the fractional representation maintains the exact value.
Significance of Remainders
In long division, we encounter remainders. The remainder represents the portion of the dividend that is left over after the division. In our example, the remainders continue to generate further decimal places, highlighting the non-terminating nature of the decimal representation. Understanding remainders is crucial in various mathematical contexts, including modular arithmetic and remainder theorems.
Applications in Real-World Scenarios
While this specific division problem might not seem immediately applicable to everyday life, the principles involved are fundamental to numerous applications. Consider scenarios involving:
-
Proportions: If you have 3 liters of paint and need to cover 58 square meters, the result helps determine how much paint is applied per square meter.
-
Unit Conversions: Converting between different units of measurement often involves division, and the concept of decimal representation becomes essential for accuracy.
-
Financial Calculations: Division is critical in calculating percentages, ratios, and various financial metrics.
-
Scientific Measurements: Precision and accuracy are paramount in scientific calculations, requiring a solid understanding of decimal representation and rounding.
Frequently Asked Questions (FAQ)
-
Q: Why is the decimal representation of 3/58 non-terminating? A: Because the fraction cannot be expressed as a fraction where the denominator is a power of 10 (e.g., 10, 100, 1000). The prime factorization of 58 includes a factor other than 2 and 5, preventing a terminating decimal.
-
Q: How many decimal places should I use in my answer? A: This depends on the level of precision required for your application. For many everyday scenarios, rounding to a few decimal places (e.g., 0.0517) is sufficient. For scientific applications or engineering, higher precision might be necessary.
-
Q: Can this division be simplified further? A: The fraction 3/58 is already in its simplest form. There are no common factors between 3 and 58.
-
Q: What if I made a mistake in my long division? A: Double-check your calculations, especially subtractions. Even a small error can propagate throughout the process, significantly impacting the final result. Use a calculator to verify your answer, but remember understanding the process is key.
-
Q: Is it always necessary to perform long division? A: No. A calculator offers a quick alternative, but understanding long division helps deepen your mathematical understanding and problem-solving skills.
Conclusion: Beyond the Numbers
This exploration of 3 divided by 58 has extended beyond a simple arithmetic problem to reveal fundamental concepts within mathematics. We've touched upon long division, decimal representation, the significance of remainders, and the practical applications of these concepts in various fields. Remember that mastering fundamental mathematical operations like division provides a strong foundation for tackling more complex problems. The understanding of decimals and fractions, their interrelation and limitations, is crucial for numerical literacy in various aspects of life. While calculators provide a quick solution, the process of solving problems manually builds critical thinking and problem-solving skills – essential abilities valuable far beyond the realm of mathematics itself. The true value lies not only in the answer (approximately 0.051724...) but in the journey of understanding the underlying principles.
Latest Posts
Latest Posts
-
180 Centigrade In Fan Oven
Sep 21, 2025
-
Where Does A Frog Hibernate
Sep 21, 2025
-
What Is A N Aquifer
Sep 21, 2025
-
Multiply And Dividing Negative Numbers
Sep 21, 2025
-
How Far Is 16 Kilometers
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 3 Divided By 5 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.