3 Divided By 3 5
dulhadulhi
Sep 23, 2025 · 5 min read
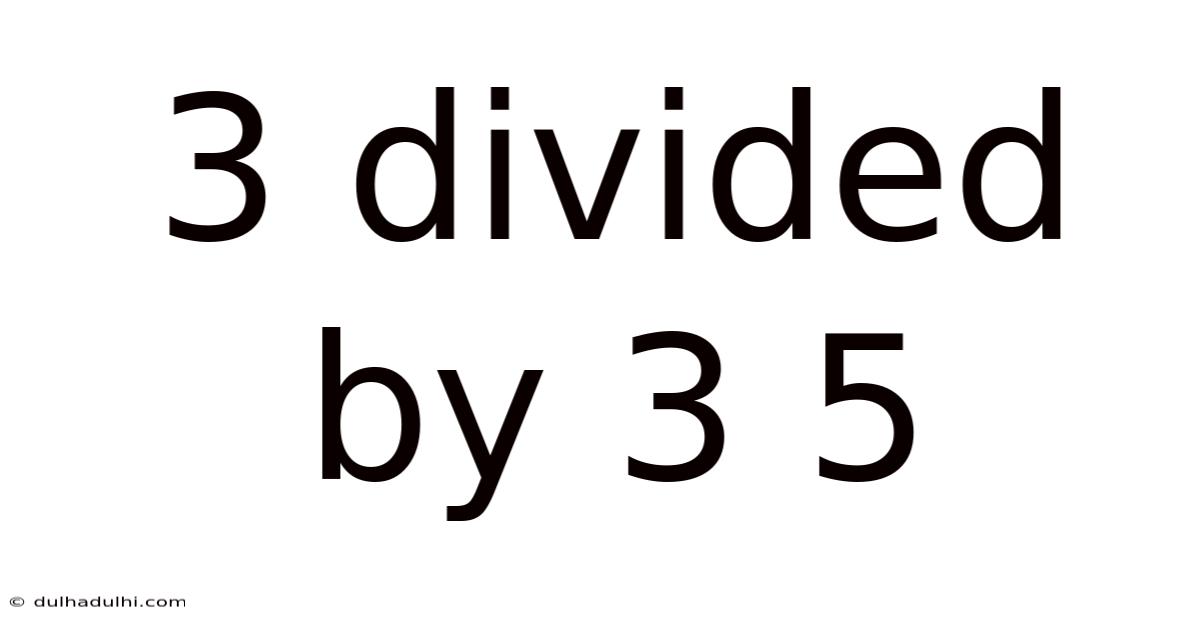
Table of Contents
Decoding 3 ÷ 3⁵: A Deep Dive into Exponents and Division
This article explores the seemingly simple mathematical expression, 3 ÷ 3⁵, providing a comprehensive explanation suitable for a wide range of readers. We'll delve into the fundamental concepts of exponents and division, examining the order of operations and ultimately arriving at the precise solution. This will cover not only the calculation itself, but also the underlying principles which govern such operations. Understanding this seemingly basic equation is a cornerstone to more advanced mathematical concepts.
Understanding Exponents
Before tackling the division, let's solidify our understanding of exponents. An exponent (also known as a power or index) indicates how many times a base number is multiplied by itself. In the expression 3⁵, '3' is the base, and '5' is the exponent. This means 3⁵ is equivalent to 3 × 3 × 3 × 3 × 3. Calculating this gives us:
3 × 3 = 9 9 × 3 = 27 27 × 3 = 81 81 × 3 = 243
Therefore, 3⁵ = 243. This understanding is crucial for solving our main problem. The exponent significantly impacts the magnitude of the number. As the exponent increases, the resulting value grows exponentially. It's important to grasp this exponential growth as it forms the basis for numerous applications in science, finance, and other fields.
The Order of Operations (PEMDAS/BODMAS)
The order of operations dictates the sequence in which we perform calculations within a mathematical expression. This is crucial to avoid ambiguity and ensure consistent results. Commonly remembered by the acronyms PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction) or BODMAS (Brackets, Orders, Division and Multiplication, Addition and Subtraction), the rules emphasize that exponents are addressed before division.
In our expression, 3 ÷ 3⁵, we first evaluate the exponent, 3⁵, which we've already determined to be 243. This simplifies our expression to 3 ÷ 243.
Performing the Division
Now, we can perform the division: 3 ÷ 243. This involves finding how many times 243 goes into 3. Since 243 is significantly larger than 3, the result will be a fraction or decimal. We can express this as a fraction:
3/243
This fraction can be simplified by finding the greatest common divisor (GCD) of 3 and 243. The GCD of 3 and 243 is 3. Dividing both the numerator and the denominator by 3, we get:
(3 ÷ 3) / (243 ÷ 3) = 1/81
Therefore, 3 ÷ 3⁵ = 1/81. This is the simplified fractional representation of the solution.
Decimal Representation
While the fraction 1/81 is perfectly accurate, it's often helpful to express the answer as a decimal. To convert 1/81 to a decimal, we perform the division:
1 ÷ 81 ≈ 0.012345679
The decimal representation is an approximation due to the repeating decimal nature of the fraction. The decimal continues infinitely with a repeating pattern.
Expanding the Understanding: Negative Exponents
Let's extend our understanding to encompass negative exponents. A negative exponent indicates the reciprocal of the base raised to the positive exponent. For example:
3⁻⁵ = 1/3⁵ = 1/243
This means that 3 ÷ 3⁵ can also be written as 3¹ ÷ 3⁵. Using the rules of exponents, when we divide numbers with the same base, we subtract the exponents:
3¹ ÷ 3⁵ = 3⁽¹⁻⁵⁾ = 3⁻⁴ = 1/3⁴ = 1/81
This demonstrates an alternative method to arrive at the same solution, reinforcing the consistency of mathematical principles.
Practical Applications: Real-world Examples of Exponents and Division
The principles illustrated by 3 ÷ 3⁵ are not merely abstract mathematical exercises. They find practical applications in diverse fields:
-
Compound Interest: Calculating compound interest involves exponents. The formula incorporates exponential growth, where the initial principal is repeatedly multiplied by a factor representing the interest rate over a specified period.
-
Scientific Notation: Scientists often utilize exponents (scientific notation) to represent extremely large or small numbers concisely. For instance, the speed of light is approximately 3 x 10⁸ meters per second.
-
Computer Science: Exponents are fundamental in computer science, particularly in algorithms and data structures. Binary numbers (base-2) utilize exponents extensively.
-
Physics: Many physical phenomena, such as radioactive decay and population growth, are modeled using exponential functions. Division is frequently used to normalize data or calculate rates of change.
-
Finance: Present value and future value calculations rely heavily on exponential functions and division. Understanding these principles is crucial for financial planning and investment analysis.
Frequently Asked Questions (FAQ)
Q1: Why is the order of operations so important in this calculation?
A1: The order of operations ensures we obtain the correct result. If we were to divide 3 by 3 before dealing with the exponent, we would get 1⁵ = 1, leading to an incorrect answer. PEMDAS/BODMAS provides a standardized approach to avoid ambiguity.
Q2: Can this be solved using a calculator?
A2: Yes, most scientific calculators can handle this calculation accurately. Simply input the expression 3 ÷ 3⁵ and the calculator will provide the correct result, either as a fraction (1/81) or a decimal approximation (0.012345679...). However, understanding the underlying principles is far more valuable than relying solely on a calculator.
Q3: What if the exponent were negative? How would that change the calculation?
A3: As explained earlier, a negative exponent signifies the reciprocal. If we had 3 ÷ 3⁻⁵, it would become 3¹ ÷ (1/3⁵) which simplifies to 3¹ × 3⁵ = 3⁶ = 729. The negative exponent fundamentally changes the outcome.
Q4: Are there other ways to express the answer besides a fraction and a decimal?
A4: While the fraction (1/81) and the decimal approximation (0.012345679...) are the most common representations, one could also express the answer using scientific notation (1.2345679 x 10⁻²) or as a percentage (approximately 1.23%). The best representation depends on the context of the problem.
Conclusion: Mastering the Fundamentals
Solving 3 ÷ 3⁵ may seem elementary, but mastering the underlying principles of exponents, division, and the order of operations is essential for tackling more complex mathematical problems. Understanding these fundamentals opens doors to a deeper appreciation of mathematics and its widespread applications across various disciplines. Remember, the seemingly simple can hold the key to unlocking profound insights. Continue to practice and explore; the world of mathematics is vast and rewarding. The journey to mathematical fluency is a continuous one, and every step forward builds a stronger foundation.
Latest Posts
Latest Posts
-
What Insects Do Ants Eat
Sep 24, 2025
-
Water Dot And Cross Diagram
Sep 24, 2025
-
Heating Curve And Cooling Curve
Sep 24, 2025
-
How Far Is 100 Feet
Sep 24, 2025
-
How Big Is 50 Ml
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about 3 Divided By 3 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.