3 Divided By 1 4
dulhadulhi
Sep 23, 2025 · 6 min read
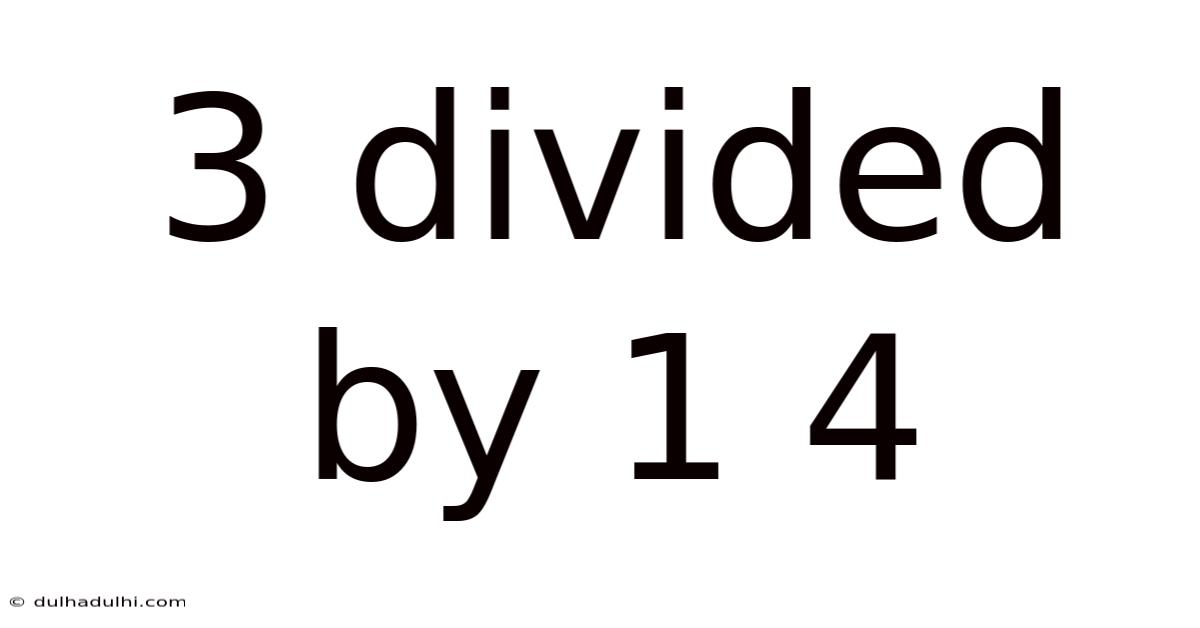
Table of Contents
Deconstructing Division: A Deep Dive into 3 ÷ 1.4
Dividing 3 by 1.4 might seem like a simple arithmetic problem, easily solvable with a calculator. However, a deeper understanding reveals fascinating connections to fundamental mathematical concepts and practical applications. This article will explore the process of calculating 3 ÷ 1.4, offering various methods, explaining the underlying principles, and delving into the broader significance of division in mathematics and beyond. We'll also address common misconceptions and answer frequently asked questions to ensure a comprehensive understanding of this seemingly simple calculation.
Understanding the Problem: 3 ÷ 1.4
At its core, the problem 3 ÷ 1.4 asks: "How many times does 1.4 fit into 3?" This seemingly straightforward question unveils the essence of division – the process of splitting a quantity into equal parts. In this case, we're splitting the quantity 3 into equal parts, each with a size of 1.4. The result will be a decimal number, indicating that 1.4 doesn't divide evenly into 3.
Method 1: Long Division
Long division provides a step-by-step approach to solving this problem, reinforcing fundamental arithmetic skills. Let's walk through the process:
-
Set up the problem: Write 3 as the dividend (the number being divided) and 1.4 as the divisor (the number by which we're dividing). Because we are dealing with a decimal divisor, it's helpful to convert it to a whole number to simplify the calculation.
-
Convert to whole numbers: Multiply both the dividend and the divisor by 10 to eliminate the decimal point in the divisor. This gives us 30 divided by 14.
-
Perform long division:
2.142... 14 | 30.000 -28 --- 20 -14 --- 60 -56 --- 40 -28 --- 12 -
Interpret the result: The result is approximately 2.142. The ellipsis (...) indicates that the decimal continues infinitely, as this is a non-terminating, repeating decimal.
Method 2: Using Fractions
Converting the decimal to a fraction offers another approach. This method emphasizes the relationship between decimals and fractions, enriching mathematical understanding:
-
Convert the decimal to a fraction: 1.4 can be written as 14/10 or simplified to 7/5.
-
Rewrite the division problem: The problem now becomes 3 ÷ (7/5). Dividing by a fraction is equivalent to multiplying by its reciprocal.
-
Invert and multiply: The reciprocal of 7/5 is 5/7. Therefore, the calculation becomes 3 × (5/7) = 15/7.
-
Convert the fraction to a decimal: To obtain a decimal representation, perform the division: 15 ÷ 7 ≈ 2.142857. This result, again, is an approximate value due to the repeating decimal.
Method 3: Using a Calculator
For practical purposes, a calculator offers the most efficient way to solve this problem. Simply enter "3 ÷ 1.4" and the calculator will provide the approximate answer: 2.14285714286.
Understanding the Remainder and Repeating Decimals
Notice that in both long division and the fractional method, we encountered a repeating decimal. This means the decimal representation doesn't terminate; the digits repeat infinitely. In the long division example, this is evident in the remainder. We continuously get a remainder that isn't zero, leading to the repeating pattern in the decimal result. This non-terminating, repeating decimal is characteristic of many divisions where the divisor and dividend don't share common factors that can simplify the fraction to a terminating decimal.
Significance of Division in Mathematics and Real-World Applications
Division is a fundamental arithmetic operation with far-reaching applications across various fields:
-
Everyday calculations: Dividing tasks among team members, splitting bills, calculating unit prices, and measuring ingredients in recipes all utilize the concept of division.
-
Science and Engineering: Division plays a crucial role in physics, chemistry, and engineering, for instance, in calculating average speed, determining concentrations, and analyzing data.
-
Computer science: Division is an essential operation in computer algorithms and programming, used for various tasks such as data processing, sorting, and resource allocation.
-
Finance: Calculating interest rates, analyzing financial statements, and determining investment returns frequently involve division.
-
Statistics: Division is used in calculating averages, variances, and other statistical measures that provide insights into data sets.
In essence, division enables us to break down complex problems into smaller, manageable parts, leading to a deeper understanding of the relationships between quantities.
Addressing Common Misconceptions
A common misconception is that division always results in a whole number. As we've seen with 3 ÷ 1.4, this isn't true; many divisions result in decimal or fractional answers. Understanding the concept of remainders and repeating decimals is key to overcoming this misconception.
Frequently Asked Questions (FAQ)
-
Q: Is the answer to 3 ÷ 1.4 exactly 2.142857?
- A: No. The answer is approximately 2.142857. The decimal representation is non-terminating and repeating, meaning it continues infinitely with the digits 142857 repeating. The result provided is rounded for practical purposes.
-
Q: Why do we get a repeating decimal?
- A: The repeating decimal occurs because the fraction 15/7 is a rational number with a denominator (7) that has prime factors other than 2 and 5. Only fractions with denominators that can be expressed as 2<sup>m</sup>5<sup>n</sup> (where m and n are non-negative integers) will result in a terminating decimal.
-
Q: What is the significance of the remainder in long division?
- A: The remainder in long division represents the portion of the dividend that wasn't evenly divided by the divisor. In the case of 3 ÷ 1.4, the continuous remainders lead to the repeating decimal in the quotient.
-
Q: Can I use a different method to solve this problem?
- A: Yes. Various methods exist, including using a calculator, converting to fractions, or employing other numerical techniques. The chosen method often depends on personal preference, the tools available, and the context of the problem.
-
Q: Are there other real-world examples where understanding 3 ÷ 1.4 would be useful?
- A: Absolutely! Imagine calculating the average speed if you traveled 3 kilometers in 1.4 hours. Or perhaps determining the cost per unit if 3 items cost $1.40. In essence, wherever you need to divide a quantity by a decimal number, a solid grasp of this concept becomes crucial.
Conclusion
The seemingly simple calculation of 3 ÷ 1.4 reveals the richness and depth of division as a fundamental mathematical operation. Understanding the various methods – long division, fractional representation, and calculator usage – and grasping the concepts of remainders and repeating decimals are crucial for a comprehensive understanding. This operation transcends simple arithmetic; it underlines the power of division in solving practical problems across a vast array of disciplines. From everyday tasks to complex scientific calculations, division remains a cornerstone of numerical understanding and problem-solving. By exploring this seemingly simple problem in detail, we gain a deeper appreciation for the elegance and utility of mathematics in our world.
Latest Posts
Latest Posts
-
How Do You Do Indices
Sep 23, 2025
-
190 Cm Is How Tall
Sep 23, 2025
-
Density Of Lead Kg M3
Sep 23, 2025
-
How Long Until 6 28 Pm
Sep 23, 2025
-
Charge Of A Silver Ion
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 3 Divided By 1 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.