1 Divided By 3 4
dulhadulhi
Sep 22, 2025 · 5 min read
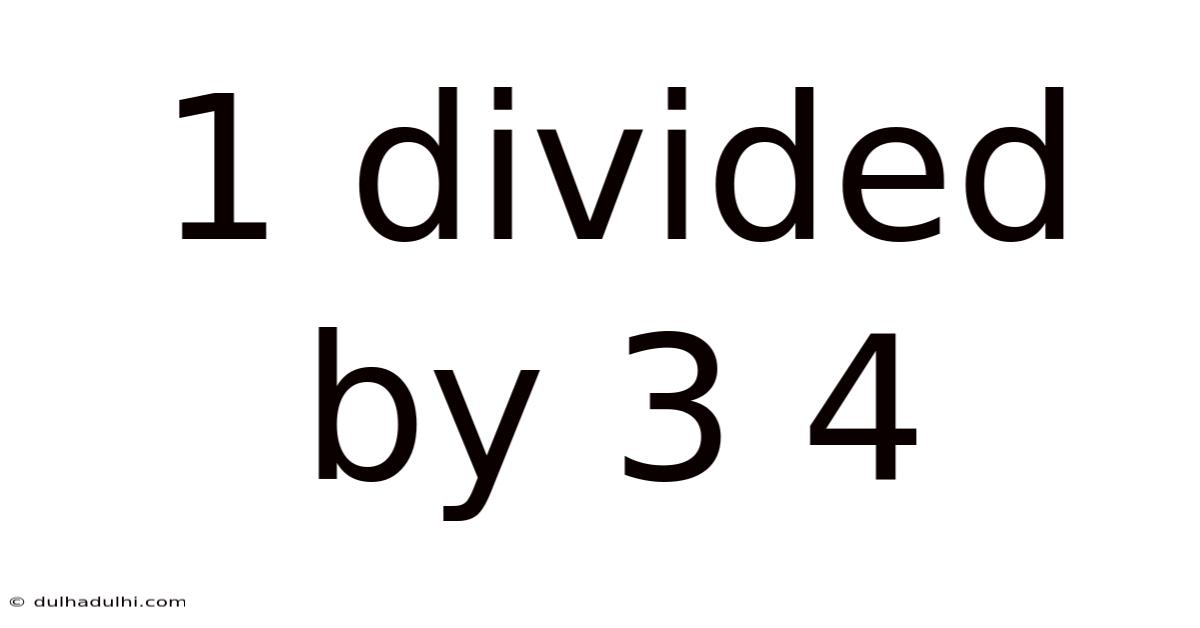
Table of Contents
Decoding 1 Divided by 3 4: A Deep Dive into Fractions and Decimal Conversions
What happens when you try to divide 1 by 3.4? This seemingly simple arithmetic problem unveils a fascinating world of fractions, decimals, and the intricacies of mathematical operations. This article will explore this division problem in detail, explaining the process step-by-step, delving into the underlying mathematical concepts, and addressing frequently asked questions. We'll also explore the practical applications of understanding such calculations.
Introduction: Understanding the Problem
The expression "1 divided by 3.4" can be written mathematically as 1 ÷ 3.4 or 1/3.4. This represents a fraction where 1 is the numerator and 3.4 is the denominator. The core challenge lies in dealing with the decimal in the denominator. We'll learn how to overcome this by transforming the fraction into a more manageable form suitable for calculation. This seemingly simple problem provides an excellent opportunity to reinforce our understanding of fundamental mathematical concepts like fractions, decimals, and long division.
Step-by-Step Calculation: From Fraction to Decimal
-
Converting the Decimal to a Fraction: The first step is to convert the decimal 3.4 into a fraction. 3.4 can be written as 3 and 4/10, which simplifies to 17/5.
-
Inverting and Multiplying: Dividing by a fraction is the same as multiplying by its reciprocal (inverse). The reciprocal of 17/5 is 5/17. Therefore, our problem becomes 1 x (5/17).
-
Performing the Multiplication: Multiplying 1 by 5/17 is straightforward: 1 x 5/17 = 5/17. This gives us our answer as a fraction.
-
Converting the Fraction to a Decimal (Long Division): To express the answer as a decimal, we perform long division: 5 divided by 17. This results in a repeating decimal: approximately 0.294117647...
The Repeating Decimal: Understanding the Nature of the Result
The result, 5/17, is a rational number, meaning it can be expressed as a fraction of two integers. However, its decimal representation is a repeating decimal. This means the sequence of digits after the decimal point repeats infinitely. In this case, the repeating block is "2941176470588". We often represent repeating decimals using a bar over the repeating sequence (e.g., 0.2941176470588235...). The length of this repeating block is a characteristic of the fraction's denominator. The number 17 has a repeating block of length 16 (the longest possible repeating block for a fraction with denominator 17).
Mathematical Explanations: Diving Deeper
The process we used highlights key concepts in arithmetic:
-
Fractions: A fraction represents a part of a whole. Understanding how to manipulate fractions is crucial in many mathematical areas.
-
Decimals: Decimals provide an alternative way to represent fractions, making some calculations easier, particularly those involving percentages or other decimal-based systems.
-
Long Division: Long division is an algorithm used to perform division with larger numbers, particularly when the division doesn't result in a whole number. It's a foundational skill in arithmetic.
-
Rational Numbers: Numbers that can be expressed as a fraction of two integers (like 5/17) are called rational numbers. They can be either terminating or repeating decimals.
-
Irrational Numbers: In contrast to rational numbers, irrational numbers cannot be expressed as a simple fraction and have non-repeating, non-terminating decimal representations (e.g., π or √2).
Practical Applications: Where This Knowledge Matters
Understanding how to handle fractions and decimals isn't just an academic exercise. It has numerous practical applications:
-
Financial Calculations: Managing budgets, calculating interest, and understanding proportions all rely on strong skills in handling fractions and decimals.
-
Engineering and Construction: Accurate measurements and calculations in engineering and construction require proficiency in decimal and fractional arithmetic.
-
Cooking and Baking: Following recipes often involves working with fractions and precise measurements.
-
Science and Data Analysis: Many scientific calculations and data analysis processes use decimal and fractional representations.
-
Everyday Life: Dividing resources fairly, sharing costs, or understanding discounts all involve basic fraction and decimal concepts.
Frequently Asked Questions (FAQs)
-
Q: Can I use a calculator for this problem? A: Absolutely! Calculators are useful tools for performing these calculations quickly and accurately, especially with repeating decimals. However, understanding the underlying process is crucial.
-
Q: Why does the decimal representation repeat? A: The repeating nature of the decimal arises from the relationship between the numerator and denominator of the fraction. When the denominator has prime factors other than 2 and 5 (the prime factors of 10), the decimal representation will generally repeat.
-
Q: How can I round off the repeating decimal? A: Depending on the required level of accuracy, you can round the repeating decimal to a specific number of decimal places. For instance, you could round 0.294117647... to 0.29, 0.294, or a greater number of decimal places based on the needed precision.
-
Q: What if the number 1 was replaced by another number, say, 7? A: The process would remain similar. You would convert 3.4 to a fraction (17/5), then multiply the given number (in this case, 7) by the reciprocal of 17/5 (which is 5/17). This would give you 35/17, which you can then convert to a decimal using long division.
Conclusion: Mastering Fractions and Decimals
Dividing 1 by 3.4, while seemingly simple, serves as a powerful illustration of fundamental mathematical concepts. This problem highlights the importance of understanding fractions, decimals, long division, and the nature of rational numbers. Mastering these concepts opens doors to a wider understanding of mathematics and its numerous applications in various aspects of life. By grasping the principles behind this simple calculation, you build a solid foundation for more complex mathematical explorations. The ability to convert between fractions and decimals fluently is a valuable skill that extends far beyond the classroom, into practical and professional contexts. Remember, the key lies not just in getting the answer but in understanding why the answer is what it is. This deep understanding empowers you to tackle more advanced mathematical problems with confidence and clarity.
Latest Posts
Latest Posts
-
What Is Relative Formula Mass
Sep 22, 2025
-
Chemical Formula For Sodium Sulfate
Sep 22, 2025
-
Armature Of An Electric Motor
Sep 22, 2025
-
How Far Is 1000 Ft
Sep 22, 2025
-
1 Metre 85 In Feet
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 1 Divided By 3 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.