1 5 Divided By 4
dulhadulhi
Sep 22, 2025 · 5 min read
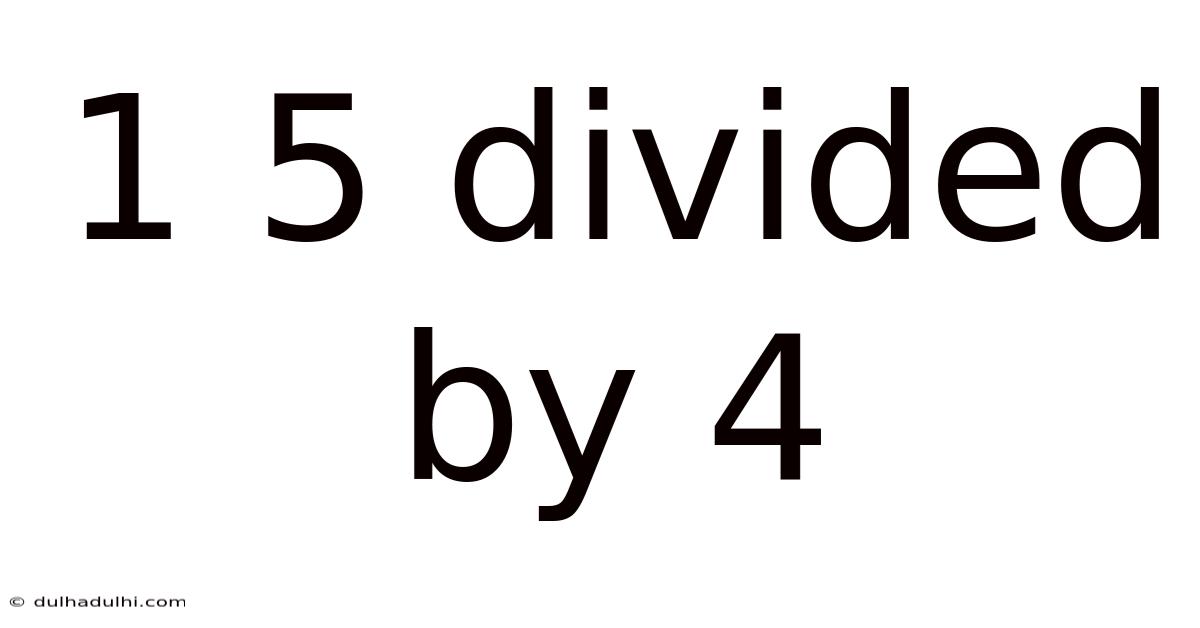
Table of Contents
Unveiling the Mystery: A Deep Dive into 15 Divided by 4
What happens when you divide 15 by 4? This seemingly simple arithmetic problem opens the door to a fascinating exploration of division, remainders, fractions, decimals, and even real-world applications. This article will not only provide the answer but also delve into the underlying concepts, offering a comprehensive understanding for learners of all levels. We'll explore various methods of solving this problem, discuss the significance of the quotient and remainder, and even touch upon advanced mathematical concepts related to division.
Understanding Division: The Basics
Division is one of the four fundamental arithmetic operations, alongside addition, subtraction, and multiplication. It represents the process of splitting a quantity into equal parts. In the context of 15 divided by 4 (written as 15 ÷ 4, 15/4, or 4⟌15), we're asking: "How many times does 4 fit into 15?"
Calculating 15 Divided by 4: Step-by-Step
Let's break down the process of dividing 15 by 4 using long division, a standard method for solving division problems:
-
Set up the long division: Write 15 as the dividend (the number being divided) and 4 as the divisor (the number dividing the dividend).
4⟌15 -
Determine how many times the divisor (4) goes into the dividend (15) without exceeding it. 4 goes into 15 three times (4 x 3 = 12). Write the '3' above the '5' in 15.
3 4⟌15 -
Multiply the quotient (3) by the divisor (4): 3 x 4 = 12. Write the '12' below the '15'.
3 4⟌15 12 -
Subtract the product (12) from the dividend (15): 15 - 12 = 3. This is the remainder.
3 4⟌15 12 -- 3
Therefore, 15 divided by 4 is 3 with a remainder of 3. This can be expressed as 3 R 3.
Interpreting the Quotient and Remainder
The result of our division, 3 R 3, consists of two key components:
-
Quotient (3): This represents the number of times the divisor (4) fits completely into the dividend (15). We can fit three whole 4s into 15.
-
Remainder (3): This is the amount left over after dividing as many times as possible. After fitting three 4s into 15, there are 3 units remaining.
Expressing the Result as a Fraction and Decimal
The remainder doesn't necessarily mean the division is incomplete. We can express the result more completely using fractions and decimals.
-
Fraction: The remainder (3) becomes the numerator of a fraction, and the divisor (4) becomes the denominator. Thus, 15 divided by 4 can be represented as the mixed number 3 ¾. This means 3 whole units and ¾ of another unit.
-
Decimal: To convert the fraction ¾ to a decimal, we perform the division: 3 ÷ 4 = 0.75. Therefore, 15 divided by 4 can also be expressed as 3.75.
Real-World Applications: Dividing 15 Items into 4 Groups
Imagine you have 15 cookies and you want to divide them equally among 4 friends. Using the long division, we find that each friend gets 3 whole cookies (the quotient). However, there are 3 cookies left over (the remainder). You could either cut the remaining cookies into fourths, giving each friend an additional ¾ of a cookie (fractional representation), or you could keep the remaining cookies for yourself or distribute them unevenly.
Exploring Further: Advanced Concepts
The simple problem of 15 divided by 4 opens up opportunities to explore more advanced mathematical concepts:
-
Modular Arithmetic: The remainder (3) is crucial in modular arithmetic, which deals with the remainders after division by a specific number (the modulus). In this case, 15 ≡ 3 (mod 4), meaning 15 is congruent to 3 modulo 4. This has applications in cryptography and computer science.
-
Euclidean Division: This theorem formally states that for any integers a (dividend) and b (divisor) where b ≠ 0, there exist unique integers q (quotient) and r (remainder) such that a = bq + r, and 0 ≤ r < |b|. Our example perfectly illustrates this theorem.
-
Rational Numbers: The result expressed as a fraction (3 ¾) or a decimal (3.75) highlights rational numbers – numbers that can be expressed as the quotient of two integers.
-
Division Algorithm: This algorithm provides a systematic procedure for performing long division. It's the foundation upon which many more complex computational algorithms are built.
Frequently Asked Questions (FAQ)
-
Q: What is the most accurate way to represent 15 divided by 4?
A: While 3 R 3 is a correct representation, 3 ¾ or 3.75 provide a more complete and precise answer, depending on the context. The fractional and decimal forms explicitly incorporate the remainder into the result.
-
Q: What if I don't use long division? Are there other methods?
A: Yes, you can use repeated subtraction. Subtract 4 repeatedly from 15 until you reach a number less than 4. The number of times you subtract 4 is the quotient, and the remaining number is the remainder.
-
Q: Can the remainder ever be larger than the divisor?
A: No. By definition, the remainder must be smaller than the divisor. If the remainder is larger, it means the divisor could have been subtracted at least one more time.
-
Q: What are some real-world examples beyond dividing cookies?
A: Numerous scenarios involve division: sharing items equally, calculating unit prices, determining average speed, splitting bills, measuring ingredients for recipes, and much more.
Conclusion: Beyond a Simple Calculation
The seemingly simple calculation of 15 divided by 4 unveils a wealth of mathematical concepts and real-world applications. From the fundamental understanding of division to advanced topics like modular arithmetic and rational numbers, this problem serves as a springboard for further exploration. Remember that the best way to represent the result depends on the context – a remainder, a fraction, or a decimal – each offering unique insights into the nature of division itself. Understanding these nuances helps develop a deeper appreciation for the power and elegance of mathematics.
Latest Posts
Latest Posts
-
Interior Angle Of A Dodecagon
Sep 22, 2025
-
How Far Is 25 Miles
Sep 22, 2025
-
Group 2 Of Periodic Table
Sep 22, 2025
-
Lcm Of 16 And 28
Sep 22, 2025
-
100 000 Minutes In Hours
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 1 5 Divided By 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.