1 1 X 1 2
dulhadulhi
Sep 22, 2025 · 5 min read
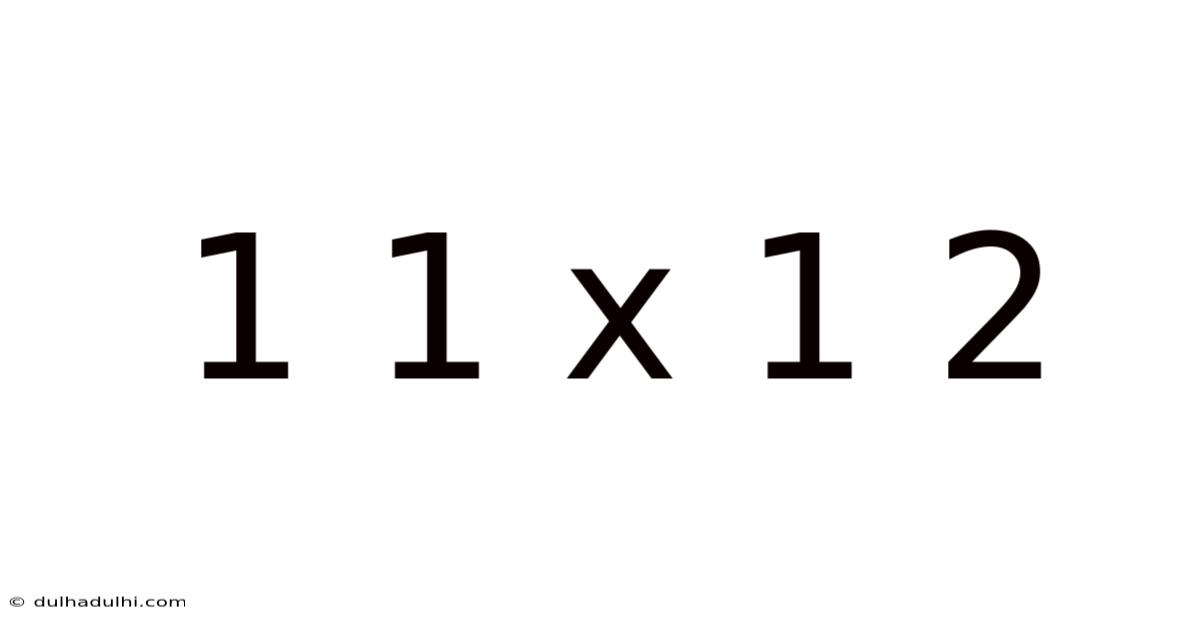
Table of Contents
Decoding 1 x 1.2: A Deep Dive into Scaling and Proportion
Understanding the seemingly simple calculation of 1 x 1.2 might seem trivial at first glance. However, this seemingly basic equation unlocks a world of applications crucial across diverse fields, from everyday budgeting to complex engineering projects. This article will explore the concept of scaling, the practical implications of multiplying by 1.2, and delve into related mathematical concepts to provide a comprehensive understanding. We'll unpack its significance beyond a simple numerical result, showcasing its role in proportional reasoning, percentage increases, and more.
Introduction: More Than Just a Calculation
The multiplication of 1 by 1.2, resulting in 1.2, might appear rudimentary. However, this calculation represents a fundamental operation in scaling and proportional reasoning. It signifies a 20% increase – a concept that finds wide-ranging applications in various scenarios, from calculating price increases and adjusting recipes to understanding economic growth and engineering design. This article aims to deconstruct this simple equation, revealing its hidden depth and practical utility. We will cover its use in different contexts and explore related mathematical concepts, making the understanding accessible to a broader audience.
Understanding Scaling and Proportional Reasoning
Scaling involves changing the size or magnitude of something proportionally. In our case, multiplying by 1.2 means scaling a quantity by a factor of 1.2, effectively increasing it by 20%. This concept is deeply rooted in proportional reasoning, a crucial mathematical skill involving understanding the relationships between quantities. When two quantities are proportionally related, a change in one quantity leads to a predictable change in the other.
For example, if a recipe calls for 1 cup of flour and you want to increase the recipe's yield by 20%, you would multiply the amount of flour by 1.2 (1 cup x 1.2 = 1.2 cups). This ensures that all ingredients are proportionally adjusted, maintaining the recipe's balance and desired outcome. The same principle applies in numerous other situations.
Practical Applications of Multiplying by 1.2
The application of multiplying by 1.2 is remarkably diverse:
-
Price Increases: Businesses frequently increase prices by a certain percentage. A 20% price increase can be easily calculated by multiplying the original price by 1.2.
-
Recipe Scaling: As mentioned earlier, adjusting recipes to serve more or fewer people often involves proportional scaling. Multiplying ingredient quantities by 1.2 increases the recipe's yield by 20%.
-
Financial Projections: In financial modeling, multiplying by 1.2 can be used to project future growth based on an assumed 20% annual increase in revenue or investment.
-
Engineering and Design: In various engineering disciplines, scaling models or blueprints by a factor of 1.2 may be necessary to adapt designs for different applications or sizes.
-
Scientific Experiments: When conducting experiments, scaling up or down the quantities of reagents often involves proportional adjustments, similar to recipe scaling.
Connecting 1 x 1.2 to Percentages
The calculation 1 x 1.2 is intrinsically linked to percentage increases. Multiplying by 1.2 is equivalent to increasing a quantity by 20%. To understand this connection, let's break down the calculation:
1.2 can be expressed as 1 + 0.2. The '1' represents the original quantity, while '0.2' represents 20% of the original quantity (0.2 = 20/100). Therefore, 1 x 1.2 = 1 x (1 + 0.2) = 1 + 0.2, signifying a 20% increase.
The Inverse Operation: Dividing by 1.2
The inverse operation of multiplying by 1.2 is dividing by 1.2. This is used to scale down a quantity by 20%, effectively finding 80% of the original value. For example, if you want to reduce a quantity by 20%, you would divide it by 1.2.
This inverse operation is equally crucial in various contexts:
-
Price Reductions: Calculating a 20% discount involves dividing the original price by 1.2.
-
Downsizing Recipes: To reduce the yield of a recipe by 20%, divide all ingredient quantities by 1.2.
-
Reverse Engineering: In engineering and design, this operation can be utilized to determine the original dimensions from a scaled-down model.
Beyond the Basics: Exploring Related Concepts
The simple calculation 1 x 1.2 opens doors to understanding more complex mathematical concepts:
-
Compound Interest: While 1 x 1.2 represents a single increase of 20%, the concept extends to compound interest calculations, where interest is added to the principal amount, leading to exponential growth over time.
-
Exponential Growth and Decay: Many real-world phenomena exhibit exponential growth or decay, where the rate of change is proportional to the current quantity. Understanding 1 x 1.2 helps lay the foundation for grasping these more complex dynamics.
-
Geometric Sequences: A geometric sequence is a series of numbers where each term is found by multiplying the previous term by a constant value (in our case, 1.2). Understanding this basic scaling factor allows for the prediction of future terms in such sequences.
Frequently Asked Questions (FAQ)
Q: How can I calculate a percentage increase other than 20%?
A: To calculate a percentage increase of 'x%', you would multiply the original quantity by (1 + x/100). For example, a 15% increase would be calculated by multiplying by (1 + 15/100) = 1.15.
Q: What if I want to decrease a quantity by a percentage other than 20%?
A: To decrease a quantity by 'x%', you would multiply the original quantity by (1 - x/100). For example, a 30% decrease would be calculated by multiplying by (1 - 30/100) = 0.7.
Q: How does this relate to compound interest?
A: While 1 x 1.2 represents a single increase, compound interest involves repeated multiplication by 1.2 (or another factor) over time. For instance, if you have a 20% annual interest rate, your principal will be multiplied by 1.2 each year.
Conclusion: The Power of Simple Mathematics
The seemingly simple calculation of 1 x 1.2 reveals a fundamental concept in scaling and proportional reasoning – a concept with far-reaching implications in diverse fields. Understanding this basic operation provides a solid foundation for grasping more complex mathematical ideas and applying them to solve real-world problems. From everyday budgeting to sophisticated engineering projects, the ability to scale quantities proportionally is an invaluable skill. This article has aimed to not only explain the calculation but also to illuminate its significance within a broader mathematical context, empowering readers with a deeper understanding of this essential mathematical tool. The seemingly insignificant 1 x 1.2 equation, therefore, opens doors to a world of mathematical possibilities and practical applications.
Latest Posts
Latest Posts
-
What Does Ion Mean Snapchat
Sep 23, 2025
-
Weight Of 1 Liter Water
Sep 23, 2025
-
Prime Factor Tree For 220
Sep 23, 2025
-
38 Inch Waist In Cm
Sep 23, 2025
-
How To Calculate Rate Constant
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 1 1 X 1 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.