0.5 X 0.5 X 0.5
dulhadulhi
Sep 24, 2025 · 6 min read
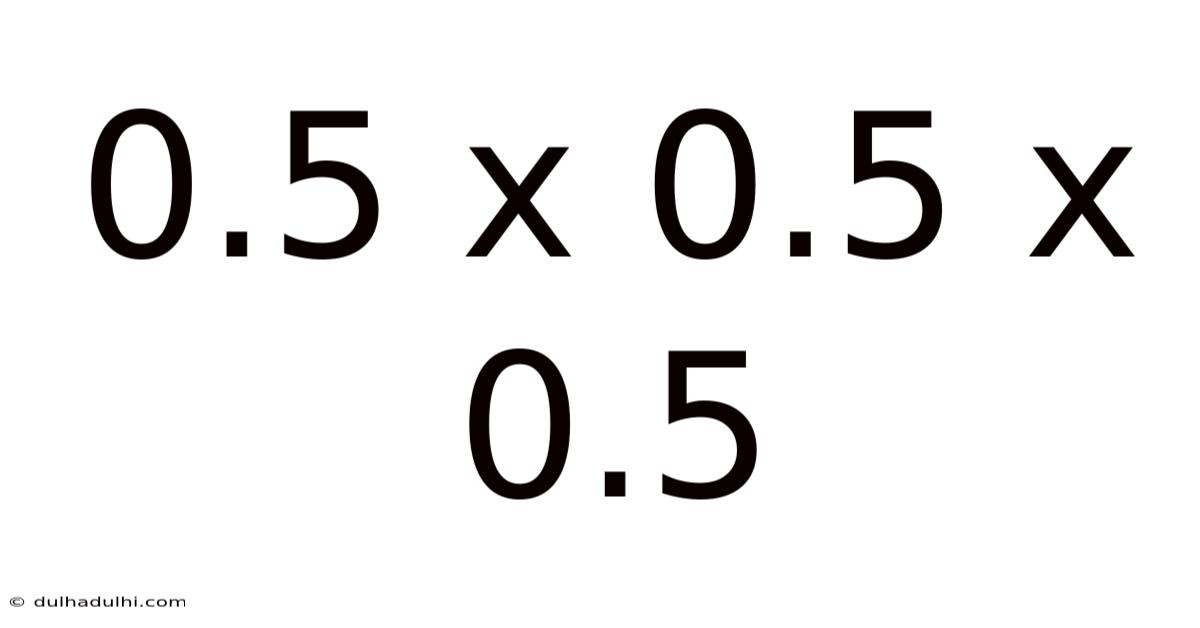
Table of Contents
Decoding 0.5 x 0.5 x 0.5: A Deep Dive into Cubic Dimensions and Beyond
This article explores the seemingly simple calculation of 0.5 x 0.5 x 0.5, delving beyond the basic arithmetic to uncover its significance in various mathematical and practical applications. We will examine the result, its implications in geometry, the concept of cubic units, and how this seemingly small calculation can have significant real-world applications. Understanding this seemingly simple equation opens doors to more complex concepts in mathematics and problem-solving.
Understanding the Calculation: 0.5 x 0.5 x 0.5
The calculation itself is straightforward: 0.5 multiplied by 0.5 multiplied by 0.5 equals 0.125. This is basic multiplication, easily performed by hand, with a calculator, or even using mental math techniques. However, the significance lies not in the act of multiplication itself, but in the context within which this calculation is applied. The numbers involved – all 0.5, or one-half – highlight a specific geometric relationship.
The Geometric Interpretation: Volume of a Cube
The most common interpretation of 0.5 x 0.5 x 0.5 involves the calculation of the volume of a cube. Each 0.5 represents the length of one side of the cube. Therefore, the calculation determines the three-dimensional space occupied by this cube. The result, 0.125, represents the volume of this cube, typically expressed in cubic units (e.g., cubic meters, cubic centimeters, cubic inches, etc.). The units depend on the units used for the side length. If the side length is 0.5 meters, then the volume is 0.125 cubic meters.
This seemingly small volume is significant because it demonstrates the relationship between linear dimensions and volume. A small change in the length of a side has a disproportionately larger effect on the volume of the cube. For instance, doubling the side length (from 0.5 to 1) increases the volume eightfold (from 0.125 to 1). This principle holds true for any cube, regardless of the side length.
Cubic Units: Understanding Three-Dimensional Measurement
The concept of cubic units is crucial for understanding volume. While linear measurements (length, width, height) are one-dimensional, and area (length x width) is two-dimensional, volume encompasses three dimensions. This is why we use cubic units – they represent a unit of measurement cubed (e.g., 1 cubic meter is a cube with sides of 1 meter each).
The result of 0.5 x 0.5 x 0.5 = 0.125 directly relates to the size of the cube. Visualizing this 0.125 cubic unit helps solidify understanding. It's a small cube, indeed, but represents a tangible amount of space. Imagine a small sugar cube; it might be approximately this size, although the exact dimensions would depend on the type of sugar and the size of the cube.
Practical Applications: Beyond the Classroom
While the calculation might seem abstract, 0.5 x 0.5 x 0.5 has several practical applications across various fields.
-
Engineering and Construction: In engineering and construction, calculating volumes is crucial for material estimation, particularly when dealing with small components or precise measurements. This calculation could be used to determine the amount of material needed to fill a small cavity, to estimate the volume of a component in a larger structure, or in various other precision engineering projects.
-
Medicine and Pharmaceuticals: The precise measurement of volume is essential in medicine and pharmaceuticals. Calculating the volume of a small container, a specific dose of medication, or a particular area within the body could involve similar calculations. This ensures accuracy and effectiveness of medical treatments.
-
3D Printing and Modeling: In the field of 3D printing and modeling, precise volume calculations are crucial for determining the amount of material used in a print and for designing precise, small-scale components. Understanding the concept of volume and the relationship between dimensions is key to optimizing the design and printing process.
-
Computer Graphics and Game Development: In computer graphics and game development, accurate volume calculations are important for creating realistic three-dimensional models and environments. This impacts the rendering of objects and the overall aesthetic and functionality of the virtual environment. Many algorithms and processes used in these fields depend heavily on precise mathematical calculations involving volume and dimensions.
-
Scientific Research: Across many scientific fields, the precise measurement of volume is crucial. This could involve anything from accurately measuring liquids to determining the volume of a sample in a scientific experiment, leading to accurate conclusions and data interpretation.
Expanding the Concept: Beyond Cubes
While we focused on cubes, the principle of multiplying three dimensions to calculate volume applies to other shapes as well, although the calculations might become more complex. Rectangular prisms, for instance, use the formula length x width x height. Understanding the fundamental concept of 0.5 x 0.5 x 0.5 lays the foundation for understanding more complex volume calculations.
Delving Deeper: Fractional Dimensions and Advanced Mathematics
The calculation 0.5 x 0.5 x 0.5 provides a gateway to more advanced mathematical concepts.
-
Fractional Dimensions: The use of 0.5 highlights the use of fractions and decimals in mathematical calculations. Understanding how fractions operate in multiplication is foundational to various advanced mathematical concepts.
-
Algebra and Variable Usage: The calculation could be represented algebraically, using variables like 'x' to represent the side length. This leads to the formula V = x³, where V is the volume and x is the side length, a fundamental concept in algebra.
-
Calculus and Rates of Change: Calculus involves the study of rates of change. Understanding how small changes in the side length of a cube (e.g., from 0.5 to 0.51) impact its volume, lays the foundation for understanding the principles of differential calculus.
-
Higher Dimensions: While we focused on three dimensions, the concept of multiplication to calculate volume can be extrapolated to higher dimensions (four, five, or even more). While difficult to visualize, these concepts are critical to various areas of advanced mathematics and theoretical physics.
Frequently Asked Questions (FAQ)
Q: What are some real-world examples where this calculation is used?
A: Many examples exist, ranging from calculating the volume of a small container in a laboratory to estimating the amount of concrete needed for a small foundation. In medicine, it could involve precise drug dosage measurements.
Q: Why is it important to understand cubic units?
A: Cubic units are essential for measuring volume, which is a three-dimensional quantity. Without them, we lack a consistent way to quantify and compare three-dimensional spaces.
Q: How does this simple calculation relate to more complex mathematical concepts?
A: This calculation is a fundamental building block for more advanced concepts. It shows the relationship between linear dimensions and volume, introduces the idea of fractional dimensions, and is a basis for understanding algebra and calculus.
Q: Can this calculation be used for shapes other than cubes?
A: Yes, while the direct application is to cubes, the principle of multiplying three dimensions applies to other shapes as well, although the formulas will vary.
Conclusion: The Power of a Simple Equation
The seemingly simple calculation of 0.5 x 0.5 x 0.5 = 0.125 offers more than just a numerical result. It provides a tangible example of volume calculation, introducing the importance of cubic units and demonstrating the relationship between linear dimensions and three-dimensional space. Understanding this basic concept opens the door to a deeper appreciation of geometry, mathematics, and its practical applications in various fields. This seemingly small calculation holds within it the potential for significant advancements in understanding and problem-solving. By exploring this simple equation, we've taken a step toward a more profound understanding of the world around us.
Latest Posts
Latest Posts
-
Assumptions Of An Ideal Gas
Sep 24, 2025
-
Lcm Of 14 And 15
Sep 24, 2025
-
Relay Sensory And Motor Neurons
Sep 24, 2025
-
3 Fractions Equivalent To 3 5
Sep 24, 2025
-
Convert 1 Pint To Milliliters
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about 0.5 X 0.5 X 0.5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.